Wheatstone-Brücke

Bildquelle: Wikipedia

Die in der Elektronik häufig zum Einsatz kommende Wheatstonebrücke ist nach dem britischen Physiker Sir Charles Wheatstone (1802 – 1875) benannt. Sie besteht aus 4 Widerständen und einem Volt- oder Amperemeter, welche wiefolgt angeordnet sind:

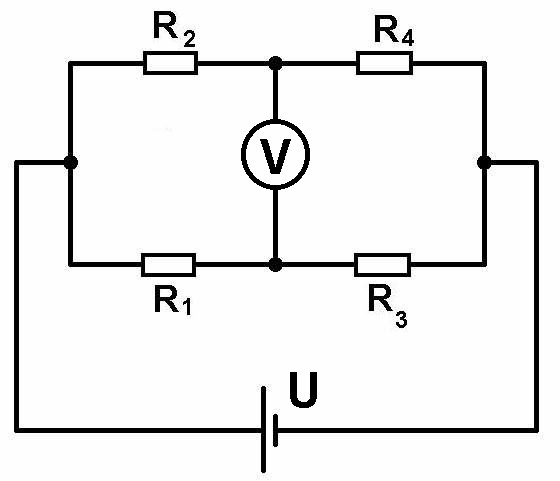
Im Falle eines Voltmeters mit seinem sehr hohen Innenwiderstand gilt für die mit dem Voltmeter gemessene Spannung:

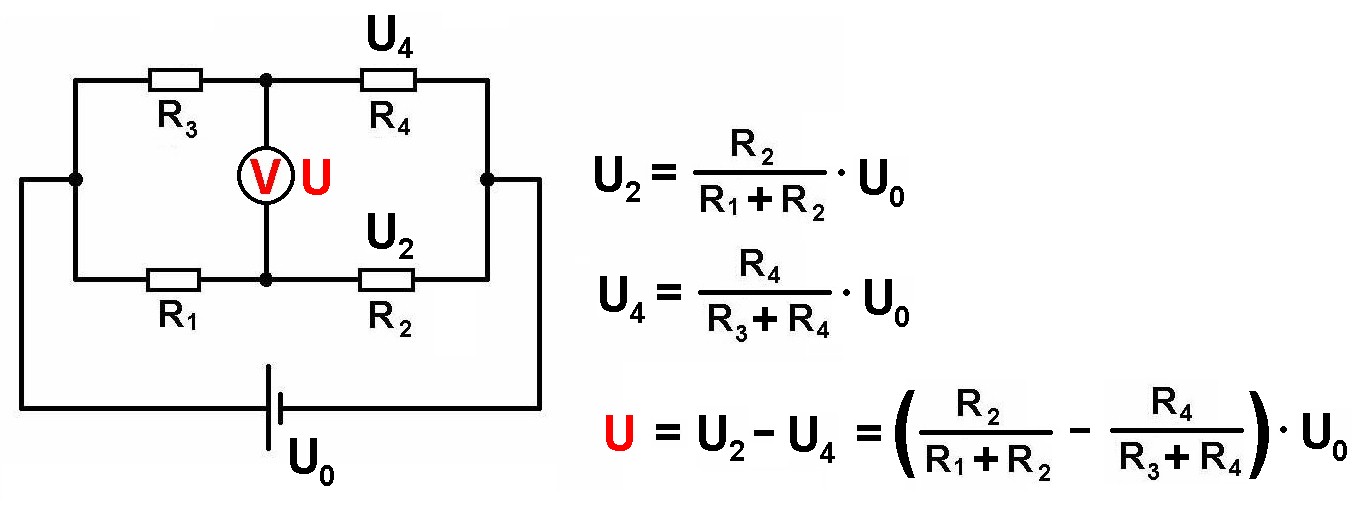
Fließt über das Amperemeter in der Mitte kein Strom bzw. zeigt das Voltmeter keine Spannung an, so gilt folgender einfache Zusammenhang:

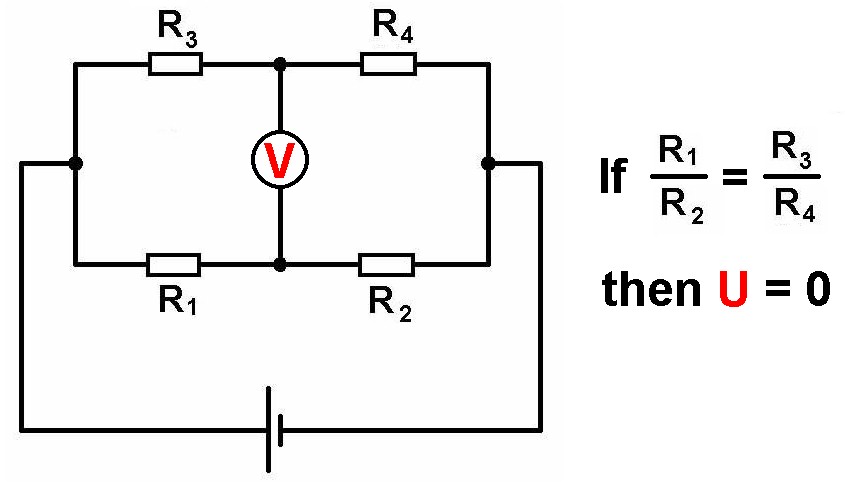
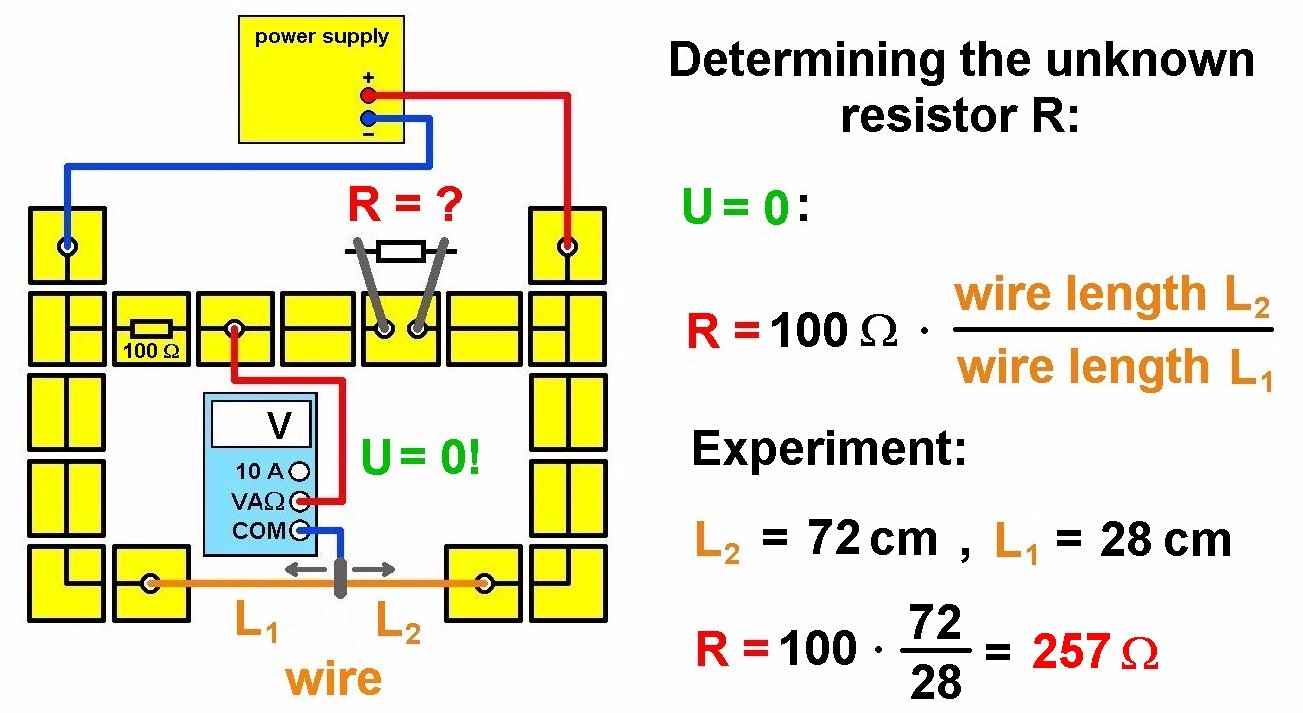
Kennt man R1 bis R3, so kann man R4 für diesen Fall ausrechnen. Anstelle der beiden Widerstände R1 und R2 kann man auch einen Draht verwenden. Ein Messkabel des Voltmeters klemmt man dann zwischen R3 und R4, während das andere so lange über den Draht geführt wird, bis das Voltmeter eben keine Spannung anzeigt:

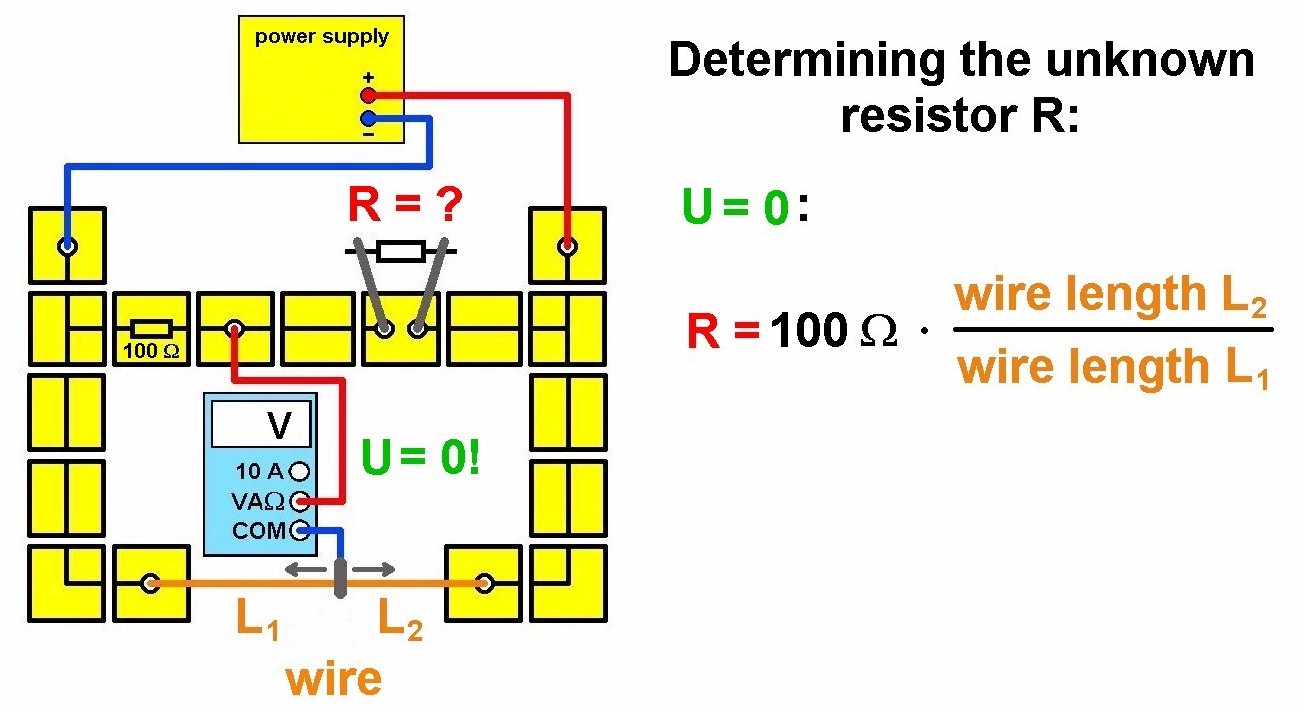
Der Widerstand eines Drahts ist ja proportional zu seiner Länge. Demnach folgt für das Verhältnis R1 / R2 = L1 / L2 und für den gesuchten Widerstand R4 = R3 · L2 / L1.

Als Draht habe ich 0.2 mm starken Konstantandraht verwendet, da dieser für Drähte einen sehr hohen Widerstand besitzt und dadurch das Netzteil nicht zu sehr belastet. Für den Widerstand R3 habe ich 100 Ω ausgewählt, daneben der unbekannte Widerstand:

Die komplette Wheatstonebrücke:

Eine Klemme des Voltmeters ist zwischen den Widerständen R3 und R4 postiert…

…die andere führe ich über den Draht, bis das Voltmeter 0V anzeigt:

Ich konnte konkret die Längen zu L1 = 28 cm und L2 = 72 cm bestimmen:

Daraus ergibt sich dann der unbekannte Widerstand R4 zu 257 Ω:

Heutzutage kann man den Widerstand natürlich bequem mit einem Ohmmeter/Multimeter bestimmen. Bei mir zeigte es einen Wert von 266 Ω an:

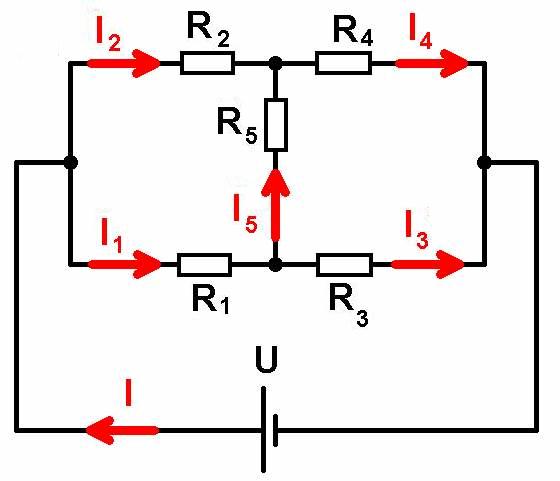
Wählt man anstelle des Voltmeters einen allgemeinen Widerstand R5, so sieht die Schaltung wiefolgt aus:

Diese habe ich mit EXCEL simuliert:

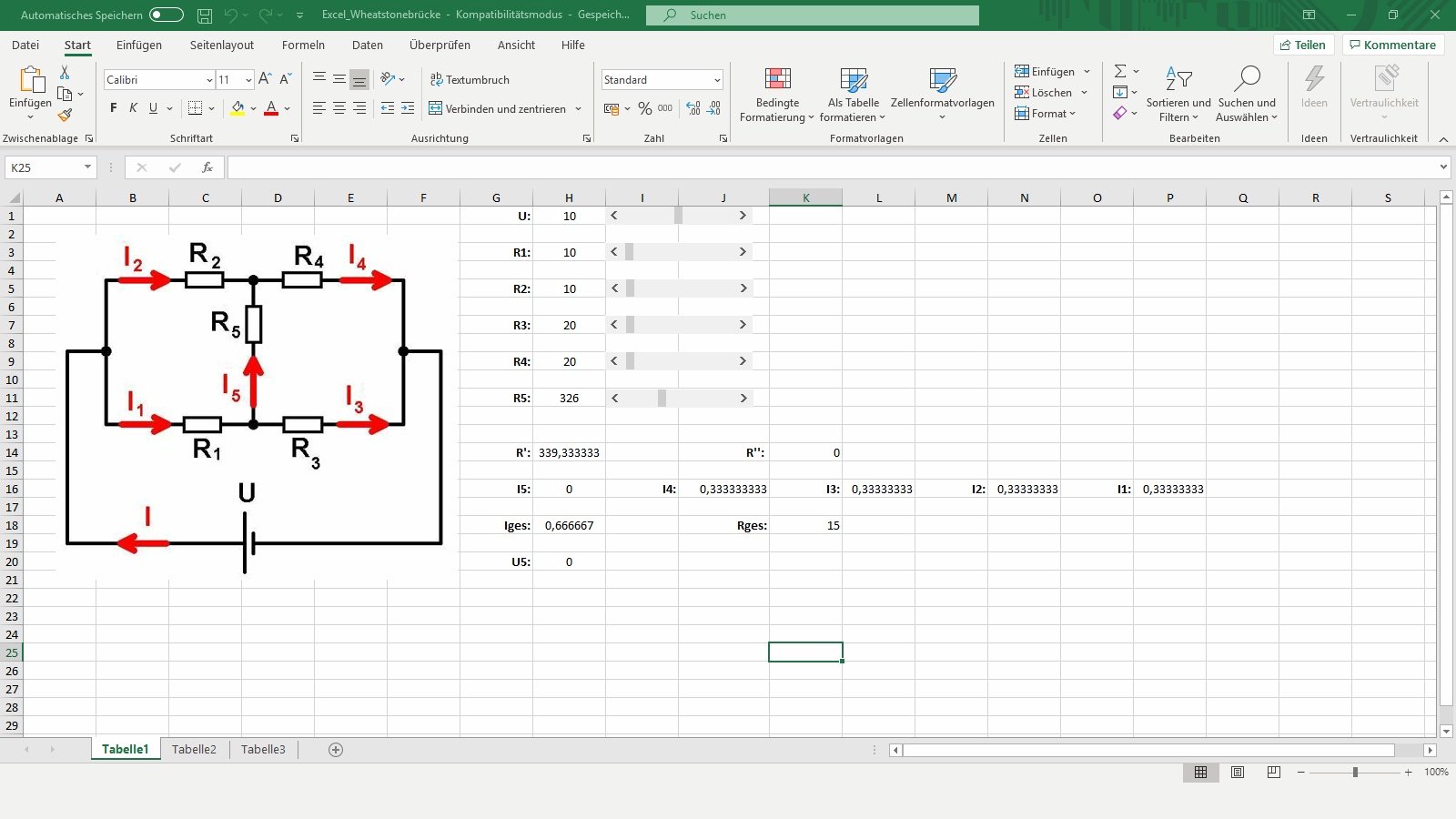
Datei: Excel_Wheatstonebrücke

Wheatstone-Brücken kommen bei meinen Projekten sehr häufig vor, hier eine Liste der Anwendungen:

Bei meiner Leistungsmesskurbel sind 4 Dehnungsmessstreifen in Form einer Wheatstonebrücke angeordnet:

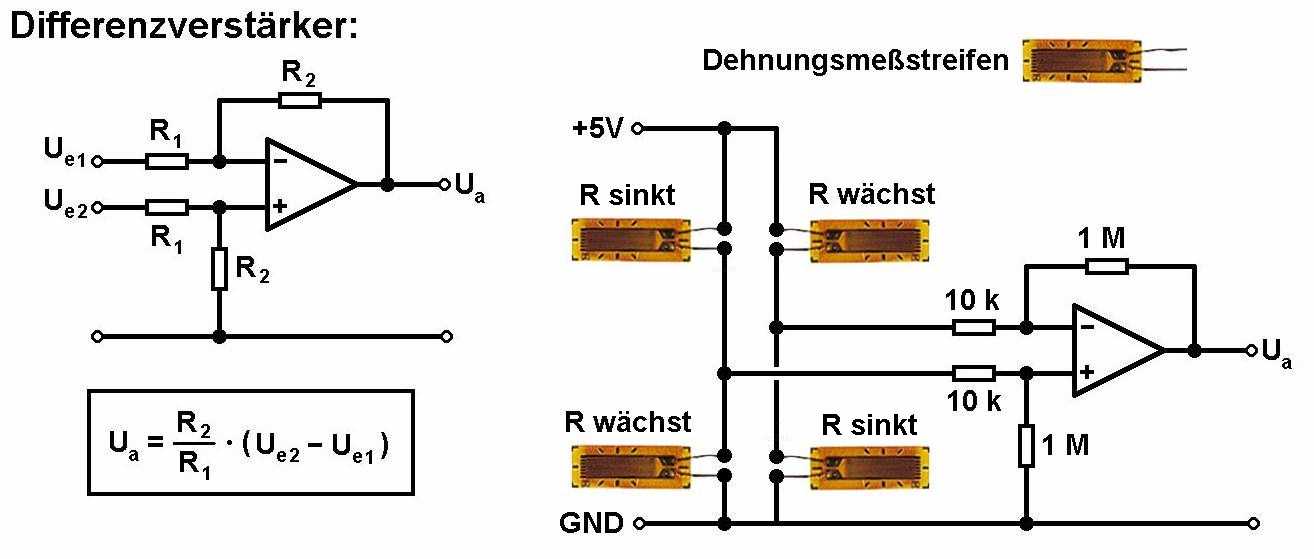
Diese Dehnmessstreifen verändern geringfügig ihren Widerstand, wenn sie gedehnt bzw. gestaucht werden. Damit man ein möglichst großes Signal an der Brücke erhält, sind die 4 Streifen wie oben abgebildet angeordnet. Jene Streifen, deren Widerstand durch die Belastung der Fahrradkurbel steigt bzw. sinkt, sind jeweils diagonal angeordnet. Auf diese Weise erhöht man die Brückenspannung. Da diese aber trotzdem noch sehr klein ist, habe ich an den Brückenausgang einen Verstärker (gain = 100) angeschlossen. Dessen Ausgangsspannung kann dann mit einem Arduino gemessen werden.

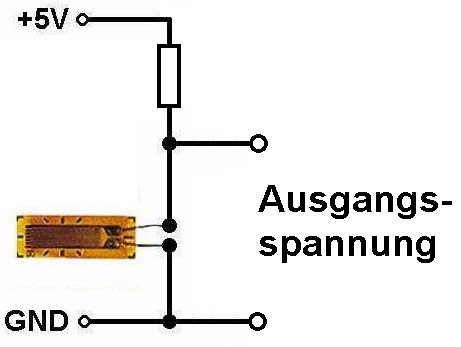
Der Vorteil einer Wheatstonebrücke liegt u.a. auch darin, dass bei zunächst noch abgeglichener Brücke die Ausgangsspannung 0 ist. Würde ich die obige simple Serienschaltung verwenden, so wäre dies nicht der Fall. Bei z.B. gleichen Widerstandswerten des oberen ohmschen Widerstands und des unteren Dehnungsmessstreifens wäre die Ausgangsspannung etwa konkret 2.5 V.

Bei meinem Pirani-Drucksensor kommt als Anzeige anstelle des Voltmeters in der Wheatstonebrücke ein Amperemeter zum Einsatz:

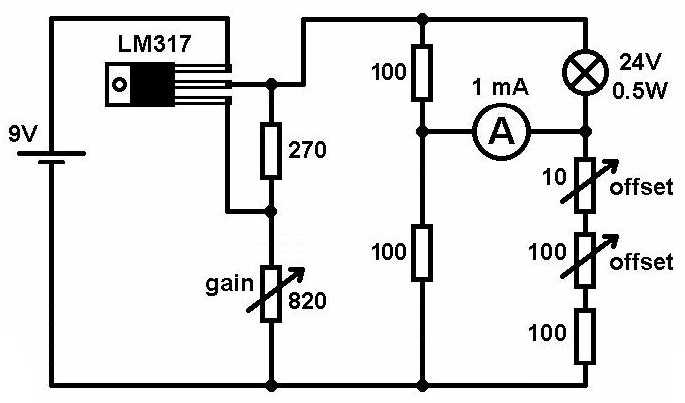
Die Wheatstonebrücke kann ich dann mit den beiden Potentiometern so abgleichen, dass bei Atmosphärendruck das Amperemeter noch keinen Strom anzeigt und der Zeiger somit von ganz links startet:

Das Youtube-Video reiche ich wie gewohnt nach…