Veränderliche Sterne werden jene Sterne genannt, deren Helligkeit (periodisch) schwankt. Es gibt unterschiedliche Typen von veränderlichen Sternen wie zum Beispiel
- Bedeckungsveränderliche Sterne
- Cepheiden
- u.a.
Bei den Bedeckungsveränderlichen Sternen kommen die Helligkeitsschwankungen aufgrund der gegenseitigen Bedeckung zweier sich umkreisender Sterne zustande. Der bekannteste Vertreter dieser Gattung ist der Stern Algol im Sternbild Perseus.
Vor rund 30 Jahren habe ich in Turbo Pascal eine Simulation programmiert. Eingegeben können die Radien der beiden Sterne, der Radius der Umlaufbahn und die beiden Intensitäten. Danach simuliert das Programm nicht nur den Umlauf, sondern berechnet automatisch die Helligkeitskurve.
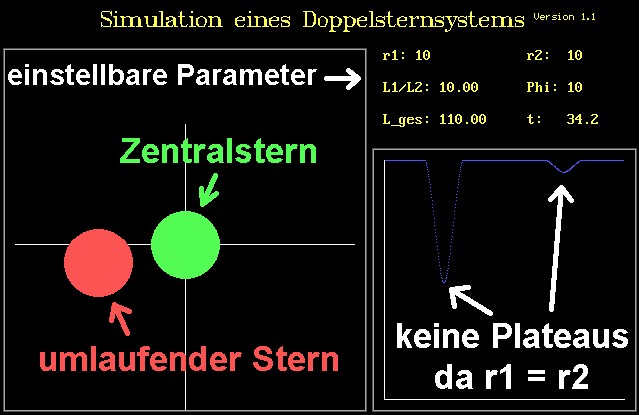
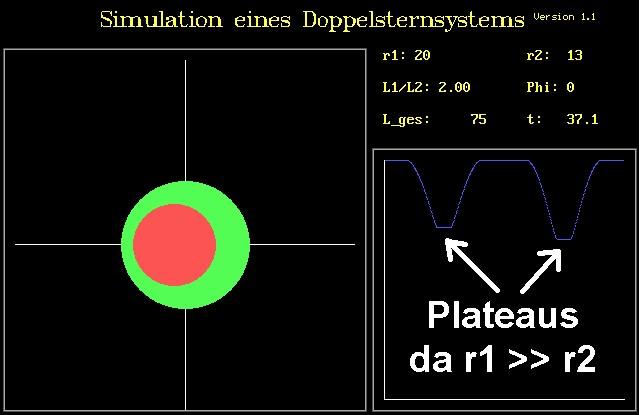
Die Mathematik dahinter ist eigentlich Schulstoff. Daher eignet sich dieses Thema auch für eine vorwissenschaftliche Arbeit im Rahmen der Matura/Abitur.

Der Schüler kann dann nicht nur die Helligkeitskurve simulieren, sondern diese auch praktisch mit einem Fotoapparat aufnehmen. Hiefür benötigt er nicht einmal eine Nachführung. Aufnahmen mit einer Belichtungszeit um die 20 Sekunden reichen völlig.

Hat der Schüler die Aufnahme im Kasten, so geht es an die Ausarbeitung. Das Astroprogamm IRIS kann ich zu diesem Zwecke sehr empfehlen. Der Schüler bestimmt damit die Pixelintensitäten mehrere benachbarter Sterne mit bekannter Helligkeit und eben die Pixelintensität von Algol.



Danach zeichnet er/sie mit diesen Werten einen Graphen + Ausgleichsgerade. Zum Schluss bestimmt er mittels dieser Geraden die momentane scheinbare Helligkeit des veränderlichen Sterns.

Konkret beträgt sie für das obere Diagramm 2.25 mag und für das nachfolgende Diagramm 2.8 mag.

Anbei zwei Photos von Algol mit stark unterschiedlichen Helligkeiten:

Mit diesen scheinbaren Helligkeiten und den bekannten Zeitpunkten der Fotografien lässt sich dann zum Schluss die Helligkeitskurve zeichnen:

Diese Messungen lassen sich eigentlich auch auf dem eigenen Balkon durchführen, so wie ich es gemacht habe. Und dies auch noch inmittel einer hellen Stadt. Astronomie kann man also (fast) überall betreiben 😉



Bei den Cepheiden haben die Helligkeitsveränderungen einen anderen Ursprung. Einfach ausgedrückt laufen bei Cepheiden vom Sternmittelpunkt in Richtung Oberfläche und wieder zurück (Schock)Wellen. Mit diesen Pulsen schwankt auch synchron die Helligkeit des Sterns. Es gibt aber einen entscheidenden Zusammenhang: Je größer der Cepheid, desto heller ist er absolut gesehen. Dadurch brauchen aber auch die Wellen länger innerhalb des Sterns und deshalb wächst in weiterer Folge die Periodendauer der Helligkeitsschwankungen. Ein Cepheid mit größerer absoluter Helligkeit hat also auch eine längere Helligkeitsperiode.

Bildquelle: https://de.wikipedia.org/wiki/Henrietta_Swan_Leavitt#/media/Datei:Henrietta_Swan_Leavitt.jpg, public domain
Auf diesen wichtigen Zusammenhang ist die Astronomin Henrietta Leavitt (1868 – 1921) gestoßen, als sie veränderliche Sterne in der großen Magellanschen Wolke beobachtet. Da die dort sichtbaren Sterne alle cirka die gleiche Entfernung zur Erde haben, ist Leavitt überhaupt erst dieser Zusammenhang aufgefallen. Das Endergebnis dieser Entdeckung war eine Beziehung zwischen der absoluten Helligkeit (= Helligkeit in 10 Parsec Abstand) eines Cepheiden und seiner Helligkeits-Periodendauer. Kennt man aber die absolute Helligkeit, so kann man mittels der scheinbaren Helligkeit (= Helligkeit von der Erde aus betrachtet) den Abstand des Cepheiden zur Erde berechnen. Cepheiden eignen sich also sehr gut als sogenannte Standardkerzen, um Distanzen im Weltall bestimmen zu können.

20 sek Aufnahme der beiden Sternbilder Cassiopeia (Bildmitte) und Cepheus (links-unten) mit dem namengebenden Cepheiden δ-Cephei


Mittels der scheinbaren Helligkeit des Cepheiden in Abhängigkeit von der Zeit bestimmt man also dessen Periodendauer. Mit dieser Periode lässt sich dann anhand obiger Abbildung seine absolute (mittlere) Helligkeit M bestimmen. Seine scheinbare (mittlere) Helligkeit m kennt man ja nun auch. Mit diesen Werten lässt sich schlussendlich die Entfernung r des Cepheiden von der Erde berechnen. Hierzu ist folgende Gleichung notwendig:
 Beispiel: δ-Cephei
Beispiel: δ-Cephei
mittlere scheinbare Helligkeit m = 3.75 mag
Periodendauer τ = 5.37 Tage ⇒ mittlere absolute Helligkeit M = – 3.48 mag
Einsetzen in die Helligkeit-Entfernung-Beziehung: 3.75 = –3.48 + 5·lg(r) – 5 ⇒ r = 279.3 Parsec = 913.3 Lichtjahre

