Führt man einem Material Wärme Q zu, so erhitzt sich dieses und seine Temperatur steigt um ΔT. Nicht jedes Material lässt sich aber gleich gut erwärmen. Während zum Beispiel Metalle schnell warm werden, benötigt man bei Wasser viel mehr Wärmeenergie.

Wie wir wissen, ist die Temperatur T eines Stoffs ein Maß für die mittlere (Bewegungs-)Energie der Teilchen. Ist die Temperatur hoch, so besitzen die Teilchen viel Energie und vice versa. In der Schule lernt man eventuell folgenden Zusammenhang zwischen kinetischer Energie E_kin der Teilchen und der Temperatur T:

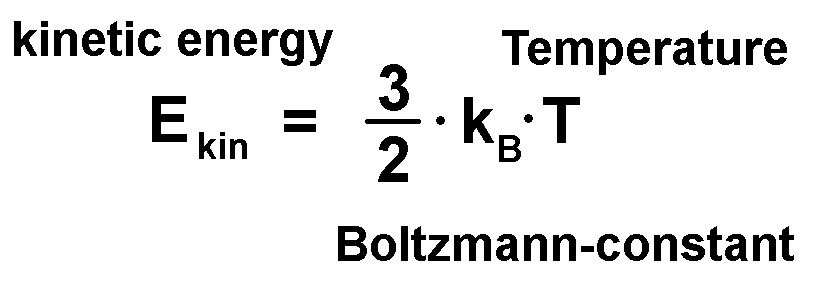
Führen wir jetzt einem Stoff bestehend aus N Teilchen die Wärmemenge Q zu, so erhält logischerweise jedes Teilchen die Menge Q/N. Genau um diesen Betrag erhöht sich dann auch dessen kinetische Energie von E_kin,alt nach E_kin,neu. Die kinetische Energie ist aber direkt proportional zur Temperatur T. Demnach erhöht sich auch die Temperatur T von T_alt nach T_neu. Es gilt also: Q/N ≡ T_neu – T_alt = ΔT. Multiplizieren wir diese Proportionalität noch mit N so erhalten wir die Beziehung: Q ≡ N · ΔT.

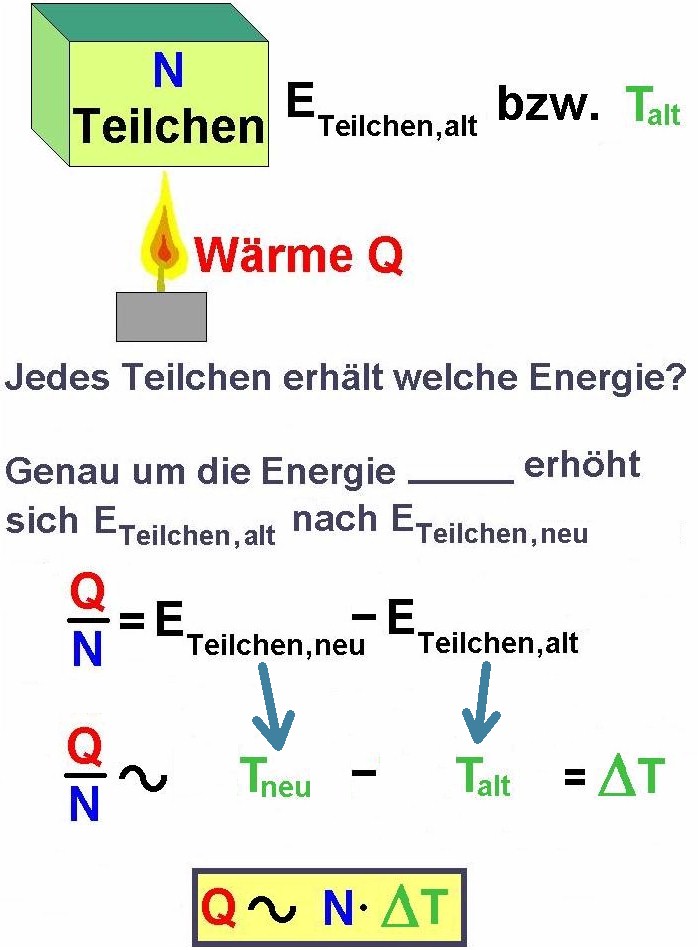
Bei doppelt so großer zugeführter Wärmemenge Q erwärmt sich der (gleiche) Körper auch doppelt so stark. Führt man aber zum Beispiel einem Körper mit doppelt so vielen Teilchen N die gleiche Wärmemenge Q zu, so führt dies nur zu einer halben Temperaturerhöhung. Dies ist aber logisch: Ein großer, schwerer Körper erwärmt sich natürlich langsamer/schwerer als ein kleiner, leichter aus demselben Material.

Die „richtige“ Beziehung/Formel zwischen Q und ΔT lautet:

Anstelle der Teilchenanzahl N tritt hier die Masse m des Körpers und als Proportionalitätskonstante die sog. spezifische Wärmekapazität c in Erscheinung. Was kann man sich aber unter dieser spezifischen Wärmekapazität c vorstellen? Nun, die zugeführte Wärme Q ist genau dann gleich dem c, wenn m = 1 kg und ΔT = 1 °C. Denn dann gilt: Q = c · m · ΔT = c · 1 · 1 = c.

Die spezifische Wärmekapazität c ist also die benötigte Wärmemenge Q, um 1 kg eines Stoffes um 1°C zu erwärmen. Ein leicht zu erwärmender Körper benötigt demnach eine geringe Wärmemenge Q, um 1 kg von ihm um 1°C zu erwärmen. Demzufolge ist auch seine spezifische Wärmekapazität c klein. Bei einem schwer zu erwärmenden Körper ist es genau umgekehrt und dessen spezifische Wärmekapazität ist groß.

Metalle sind leicht zu erwärmen und besitzen daher ein kleines/niedriges c. Wasser lässt sich hingegen sehr schwer erwärmen und verfügt über ein sehr großes c, konkret c_Wasser = 4150 J/kg·°C. Dieser Wert entspricht übrigens genau 1000 cal/kg·°C. Um 1 kg Wasser um 1°C zu erwärmen benötigt man also 4150 J = 1000 cal (Kalorien). Für 1 g Wasser ist es demnach genau 1 Kalorie (cal).

Übrigens: Lässt sich ein Körper nur sehr schwer erwärmen, benötigt man also pro Kilogramm und pro °C sehr viel Wärmeenergie. Im schwer zu erhitzenden Körper steckt dann aber wiederum sehr viel Wärme, wenn er denn dann warm ist. In warmen Wasser steckt daher ungleich mehr Wärmeenergie als im gleich warmen Metall. Wasser ist also ein ausgezeichneter Energieträger/speicher. Dies hat weitreichende Konsequenzen. So wird etwa unser Klima auf der Erde entscheidend durch die in Wasser gespeicherte Wärme beeinflusst. Am Meer (maritimes Klima) ist es zum Beispiel oftmals noch bis in den Spätherbst viel wärmer als im Landesinnere (kontinentales Klima), da die große Menge der im Wasser gespeicherten Wärme erst langsam abgegeben wird.

In diesem Experiment geht es um die Bestimmung der spezifischen Wärmekapazität von Wasser. Dazu führe ich dem Wasser konkret elektrische Energie zu. Zwischen Spannung U, Stromstärke I und elektrischer Leistung P besteht ja der wichtige Zusammenhang: P = U · I. Die Leistung P entspricht der pro Sekunde umgesetzten Energie, hier konkret Wärme. Es gilt also auch: P = Q/t bzw. Q = P · t. Mit der nun bekannten Formel für die spezifische Wärmekapazität folgt: Q = P · t = c · m · ΔT. Links vom Gleichheitszeichen wächst also (bei konstanter Leistung P) die zugeführte Wärmemenge linear mit der Zeit t an. Daher muss auch die rechte Seite, sprich die Temperaturerhöhung ΔT linear mit der Zeit t zunehmen. Wir erhalten also idealerweise folgenden Graphen:

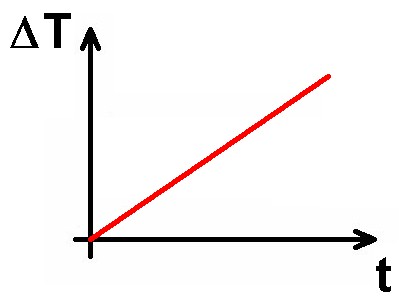
Formt man die Gleichung P · t = c · m · ΔT nach ΔT um, so erhält man: ΔT = (P / [c · m]) · t. Dies ist aber eine Geradengleichung mit dem Anstieg k = P / (c · m). Bestimmt man daher experimentell k und kennt die zugeführte elektrische Leistung P und die Masse m, so kann man die unbekannte spezifische Wärmekapazität c berechnen. Genauso werde ich es auch machen…

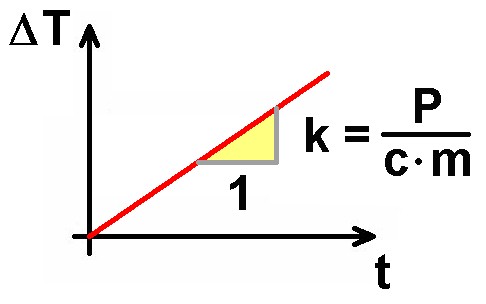
Für den Versuch benötigt man Leistungswiderstände, ein Netzteil wenn möglich mit Spannungs- und Stromanzeige, ein Gefäß mit Wasser und ein Thermometer.

Mein vielgenutztes Laptopnetzteil:

Die beiden 1 Ω Leistungswiderstände, welche ich seriell verschaltet habe (R_ges = 2 Ohm):

Die Waage zur Bestimmung der Wassermasse m:

Es gilt also: m = 0.43 kg.

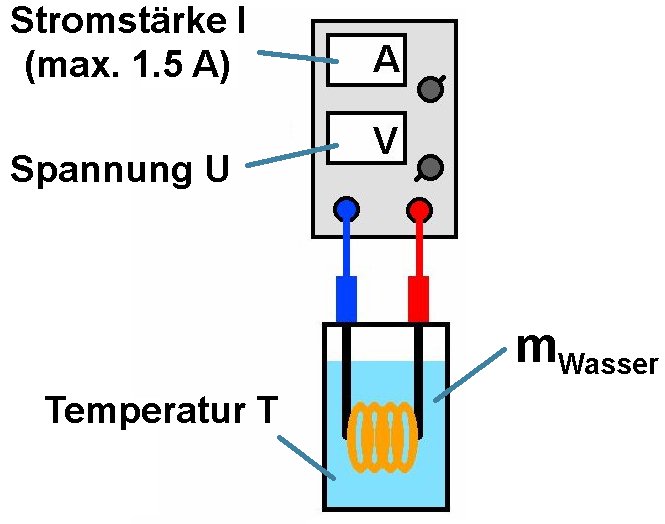
Der gesamte Versuchsaufbau, wobei das Gefäß mit dem Wasser natürlich nicht mehr auf der Waage hätte stehen müssen:

Sodann wurde eine gewisse Spannung U eingestellt, die Stromstärke I abgelesen und in bestimmten Zeitabständen die steigende Wassertemperatur notiert:

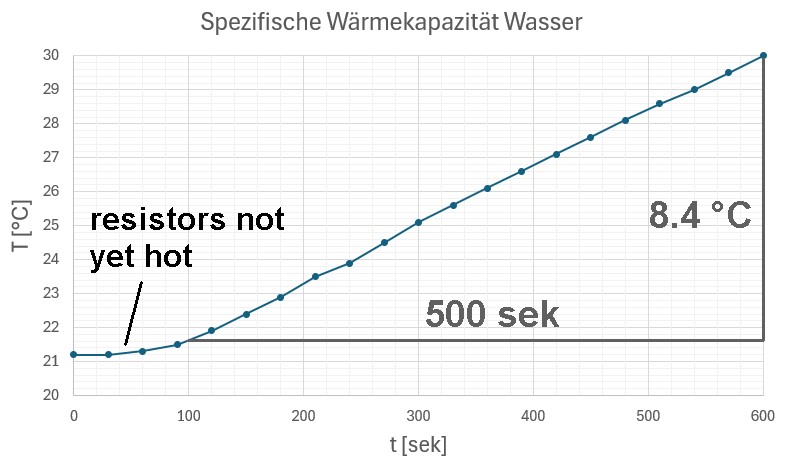
Zu Beginn erhalte ich noch keine ansteigende Gerade, da die Widerstände erst einmal selbst warm werden müssen. Danach steigt der Graph aber schön linear an. Innerhalb von t = 500 sek wächst die Temperatur um ΔT = 8.4 °C. Für den Anstieg k gilt daher: k = 8.4 /500.

  Die einfache Rechnung zur Ermittlung der spezifischen Wärmekapazität c:

Mein experimentell erhaltener Wert für die spezifische Wärmekapazität von Wasser liegt logischerweise über dem Sollwert. Deshalb logisch, weil die zugeführte Energie nicht gänzlich in die reine Erwärmung des Wassers fließt. Durch diese Verluste ist die scheinbar zur Erwärmung notwendige Wärmemenge immer größer als der theoretische Wert.

---

Kleiner Nachtrag zu den sog. Freiheitsgraden f:

Die Eingangs erwähnte Formel E_kin = 3/2 · k_B · T ist ein Spezialfall für das ideale Gas mit genau 3 Freiheitsgraden. Freiheitsgrade sind sozusagen die Kanäle eines Atoms/Moleküls, in die Energie fließen kann. Bei einem idealen Gas, welches nur über reine kinetische Energie der Translation verfügt, sind dies genau 3 Kanäle und zwar die Translationsenergie in x-, y- und z-Richtung.

Ein Molekül kann zum Beispiel zusätzlich zu diesen Energiekanälen der Translation noch über Schwingungsenergien verfügen. Die Anzahl der Freiheitsgrade f ist daher zumeist größer als 3!

Eigentlich gilt folgender Zusammenhang zwischen der Energie eines einzelnen Freiheitsgrads und der Temperatur T:

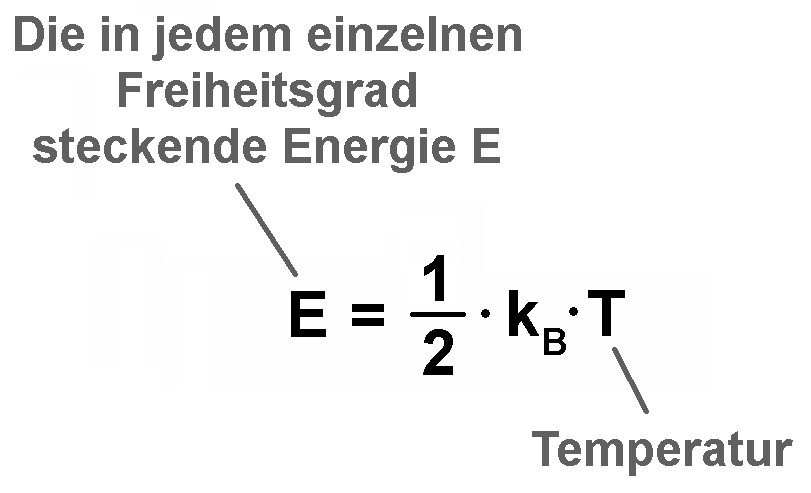
Wenn sich die zugeführte Wärme Q auf N Teilchen verteilt, so erhält nach wie vor jedes Teilchen/Atom/Molekül die Energie Q/N. Nun fließt aber diese Wärmemenge Q/N in alle vorhandenen f Freiheitsgrade des Teilchens/Atoms/Moleküls. Bei vielen Freiheitsgraden f bleibt daher pro Freiheitsgrad nur eine geringere Energie übrig als bei wenigen Freiheitsgraden. Daher erhöht sich die Temperatur T bei einem Teilchen mit vielen Freiheitsgraden nur wenig. Ein Teilchen mit vielen Freiheitsgraden besitzt demzufolge eine höhere spezifische Wärmekapazität c! Es gibt also einen Zusammenhang zwischen c und f. Genau diesen leite ich nun her:

Eigentlich sollte Wasser als Molekül mit 3 Atomen nur über f = 9 Freiheitsgrade besitzen. Woher also dieser Unterschied? Bei hohen Temperaturen wird die thermische Energie k_B·T groß genug, um auch die quantisierten Schwingungszustände der Moleküle zu besetzen. Jedes Schwingungsfreiheitsgrad trägt dann sowohl kinetische als auch potenzielle Energie bei. Dadurch erhöhen sich die effektiven Freiheitsgrade von f = 9 (Translations-, Rotations-, und Schwingungsmoden kombiniert) auf f = 18!

Man erkennt deutlich an der theoretischen Formel für c ≡ f, dass ein Molekül mit vielen Freiheitsgraden eine große spezifische Wärmekapazität besitzt und vice versa. Man erkennt an diesem konkreten Beispiel aber auch sehr gut, dass die Physik in Wahrheit viel komplizierter ist, als man zunächst auf Basis der vereinfachten Schulphysik meinen würde 😉