Bei diesem Versuch geht es darum zuerst experimentell und dann mittels Computer die schnellste Kugelbahn bei gegebenen Start (0/0.2m) und Ziel (0.8m/0) zu ermitteln. Die Schüler merken schnell, dass die Verbindungsgerade zwischen Start und Ziel nicht die schnellste Verbindung ist.

Die Kugelbahn selbst ist aus einem flexiblen Kabelkanal vom Baumarkt gefertigt. Die Neigung der Bahn im Start- und Zielpunkt kann stufenlos verstellt werden. Damit eine solche Verstellung keinen Einfluss auf die exakte Start- und Zielposition hat, befindet sich diese genau in der Drehachse der Verstellung. Da sich bei Veränderung der Neigung natürlich auch die Bahnlänge verändert, muss die Kugelbahn natürlich in der Halterung verschoben werden können. Trotz einer gewissen Eingeschränktheit lassen sich mit dieser Methode sehr viele unterschiedliche Bahnformen festlegen.

Die Laufzeit der Kugel wird einfach mit einer Stoppuhr mehrfach bei unveränderter Bahn bestimmt und daraus der Mittelwert berechnet. Konkret liegen die besten Laufzeiten bei ca. 0.5 Sekunden.

Im zweiten Teil lässt man nun den Computer die schnellste Bahn berechnen. Hierzu habe ich ein Programm in Visual Basic geschrieben. Zuerst aber noch zur Theorie des Experiments:

Es sei darauf hingewiesen, dass bei der Herleitung der Laufzeit die Reibung der Kugel vernachlässigt wurde. Die Integrale werden numerisch mittels Trapezsummenverfahren berechnet. Dabei verwende ich rund 1000-10000 Stützstellen auf der x-Achse, was eine hinreichende Genauigkeit liefert.

Wie man anhand der Schlussformel (2.5) sieht, benötigt man zur Berechnung der Laufzeit nur die Bahnfunktion y(x). Aber wie weiß nun der Computer, welche Funktion er nehmen soll? Es gibt ja unendlich viele verschiedene Funktionen…

Nun bei meinen Berechnungen schränke ich die zu untersuchenden Bahnfunktionen y(x) auf reine Polynome vom Grad n <= 4 ein. Dies ist aber für den Computer noch immer nicht einschränkend genug. Deshalb müssen die Schüler die Grenzen der zu verwendenden Koeffizienten der Polynomfunktion und deren Schrittweite eingeben. Hier sieht man die Bedienoberfläche des Programms:

Links oben werden die Grenzen und Schrittweiten für die Koeffizienten b, c und d eingegeben. Der Koeffizient a ist bei einem Polynom der Funktion y(x) = a + b·x + c·x² + d·x³ + e·x^ 4 aber durch den Startpunkt (0/0.2m) mit 0.2 festgelegt. Ebenso der Koeffizient e, da ja die Bahn zwingend durch den Endpunkt (0.8m/0) gehen muss. Bleiben also nur noch die Koeffizienten b, c und d zur freien Auswahl.

Drückt man auf Start, so geht der Computer alle möglichen Kombinationen der Koeffizienten b, c und d durch und berechnet jeweils die Rollzeit t. Die beste/schnellste Laufzeit gibt er dann gesondert im Fenster unten links aus. Dieses (vorläufige) Ergebnis kann dazu genutzt werden, die Bereiche der Koeffizienten weiter einzuschränken, dafür mit feinerer Schrittweite.

Die beste/schnellste Bahn wird dann vom Programm auch noch rechts unten grafisch dargestellt.

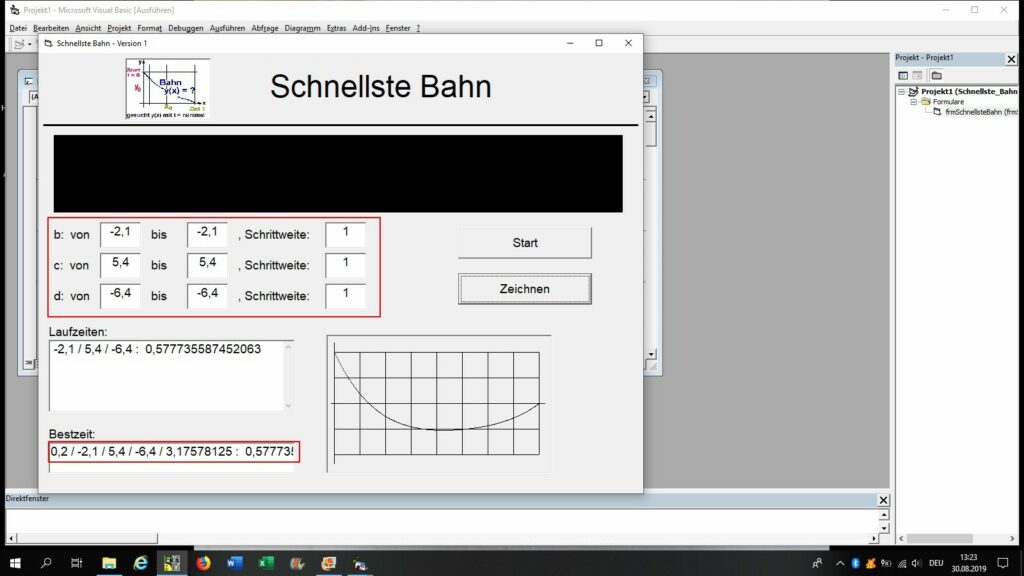
Die Dauer der Berechnungen ist nicht gerade kurz. Bei 1000 Stützstellen für das Integral und 7 · 21 · 21 = 3087 verschiedenen Koeffizienten-Kombinationen braucht der Computer bereits über 2 Minuten Rechenzeit:

Ich habe auch noch eine Messreihe mit unterschiedlichen Polynomgraden gemacht. Dabei habe ich für jeweils den Grad n = 1, 2, 3 und 4 die schnellste Kugelbahn ermittelt und dann alle Lösungen grafisch dargestellt:

Für den Grad 1 (= lineare Funktion) gibt es logischerweise nur eine einzige Kugelbahn, welche die Bedingung durch Start und Ziel zu verlaufen auch erfüllt. Bei höheren Graden hat man natürlich eine Vielzahl an möglichen Funktionen zur Auswahl. Wie man an der Grafik erkennen kann, verlaufen die besten/schnellsten Bahnen weit im negativen y-Bereich. Dadurch vergrößert sich zwar die Länge der Kugelbahn, aber die durchschnittliche Geschwindigkeit wächst ebenso und gleicht den längeren Weg aus, sodass sich trotzdem eine bessere Laufzeit ergibt.

Die Schüler müssen dann zum Abschluss das vom Computer ermittelte beste Polynom in dasselbe Diagramm einzeichnen, in dem sie schon die experimentell ermittelte beste Bahn eingezeichnet haben. Im Idealfall unterscheiden sich beide Kurven dann nur geringfügig voneinander…