Hier (https://stoppi-homemade-physics.de/ultraschall/) habe ich eine Methode vorgestellt, mittels Arduino und dem Utraschallmodul HC-SR04 die Schallgeschwindigkeit zu bestimmen.
Es gibt aber noch weitere Experimente, mit denen man die Schallgeschwindigkeit ermitteln kann.
Variante 1
Für diese Variante benötigt man 2 Stück Soundmodule mit Elektretmikrophon, eine externe Soundcard, Klinkenkabel und -buchsen für eine einfache Audioweiche bzw. 2 Stück Liion-Zellen zur Stromversorgung der Soundmodule. Zur Auswertung wird noch die kostenlose Software Audacity (https://www.audacity.de/) benötigt.





Hier ist der gesamte Aufbau zu sehen:


Man legt die beiden Mikrophone/Soundmodule in einem bekannten Abstand d voneinander auf den Boden. Danach klatscht man mit den Händen einmal kräftig.
Hinweis: Die Schallquelle (die Hände) müssen sich in der Verlängerung der beiden Mikrophone befinden und mit den Händen sollte auch knapp über dem Boden geklatscht werden. Nur dann ist der Wegunterschied der Schallwellen auch tatsächlich gleich dem Abstand d!
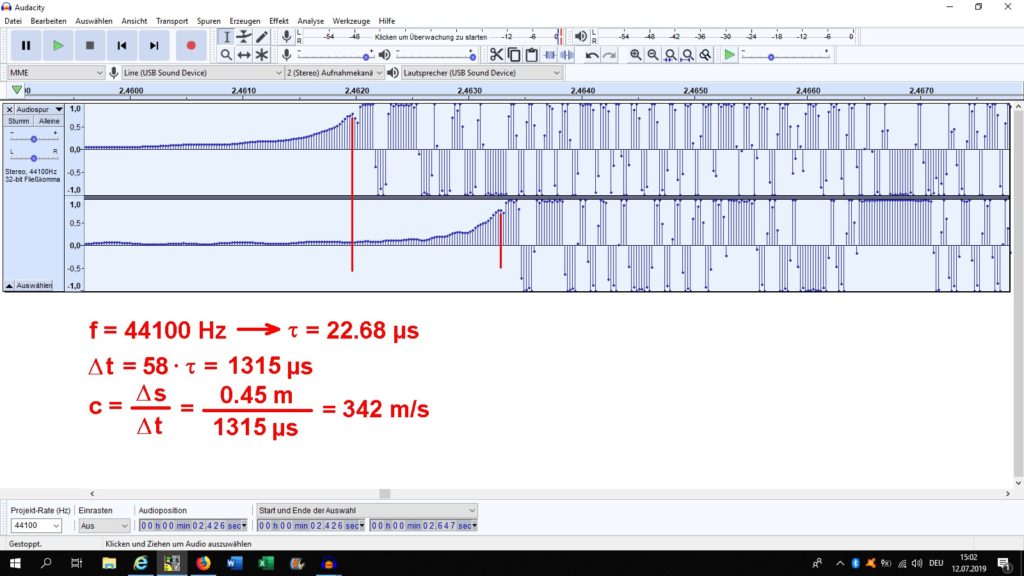
Mit der Software Audacity nimmt man nun diesen Klatschen auf, wobei jedes der beiden Mikrophone einen Audiokanal (left/right) belegt. Wenn man alles richtig gemacht hat, erkennt man bei einer Tonspur ein verzögertes Einsetzen des Signals. Mittels der bekannten Abtastrate (engl. sampling-rate) zum Beispiel von 44.1 kHz und der Taktverzögerung (z.B. setzt das zweite Signal um 58 Takte später ein) lässt sich die Zeitverzögerung Δt bestimmen. Aus d und Δt folgt dann für die Schallgeschwindigkeit: c = d / Δt.
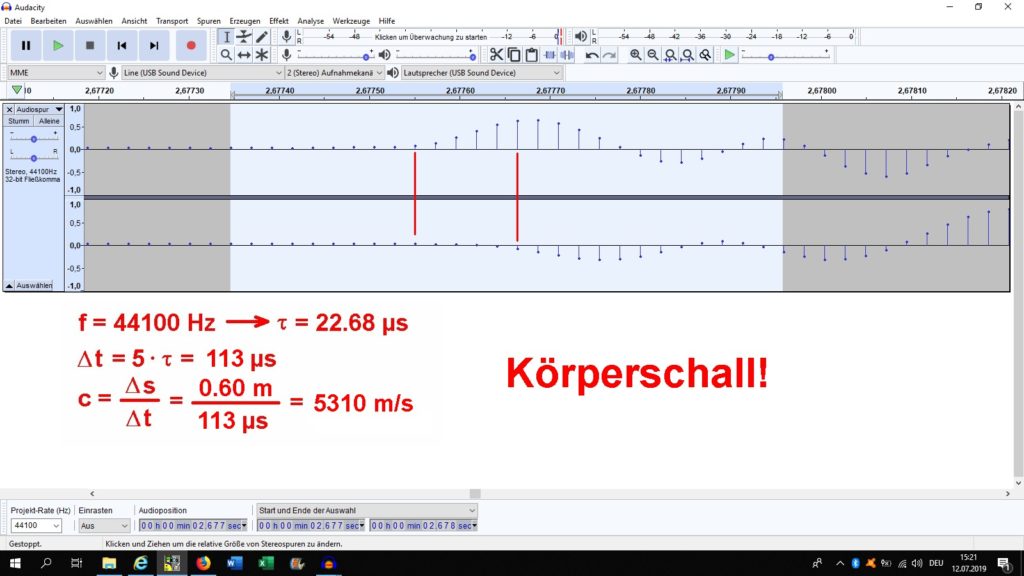
Legt man die Soundmodule vertikal auf den Boden, sodass die beiden Elektretmikrophone den Boden bedecken und stößt dann in einiger Entfernung mit der Faust auf den Boden, so kann auch auf gleiche Weise wie oben geschildert die Schallgeschwindigkeit in einem Körper (konkret dem Zimmerboden) bestimmt werden. Man wird feststellen, dass hier die Schallgeschwindigkeit deutlich höher ist als in Luft!

Variante 2
Auch mit diesem Versuch lässt sich die Schallgeschwindigkeit zumindest näherungsweise bestimmen. Benötigt wird ein Glasrohr mit einem Durchmesser von rund 3-4 cm und einer Länge L von ca. 50 cm. Ich habe hierfür eine Leuchtstoffröhre verwendet. Beim Öffnen der Röhre muss man vorsichtig umgehen. Erstens weil sonst die Röhre sehr ungleichmäßig abreißt und zweitens weil sich innerhalb der Röhre Quecksilber befindet!
Daher die Röhre nur im Freien oder einem sehr gut gelüfteten Raum öffnen und den direkten Kontakt mit der Leuchtschicht im Inneren unbedingt vermeiden und diese dann auch restlos entsorgen!


Zum Öffnen habe ich einen Glasschneider bzw. eine Trennscheibe für den Dremel verwendet. Aber selbst mit diesem Werkzeug gelingt es mehr schlecht als recht die Glasröhre schön glatt ohne Risse zu öffnen…



In dieses Glasrohr klemmt man nun nahe einem Rohrende ein ausgeschnittenes Metallsieb (z.B. von einem Teesieb).



Hält man nun das Glas kurz über einen Bunsenbrenner und erhitzt das Sieb bis es glüht, so entsteht ein schöner, klarer Ton wie bei einer Orgelpfeife. Mit einer Handy-App (z.B. dem Sound Analyser) kann zum Beispiel die Frequenz f dieses Tons bestimmt werden.
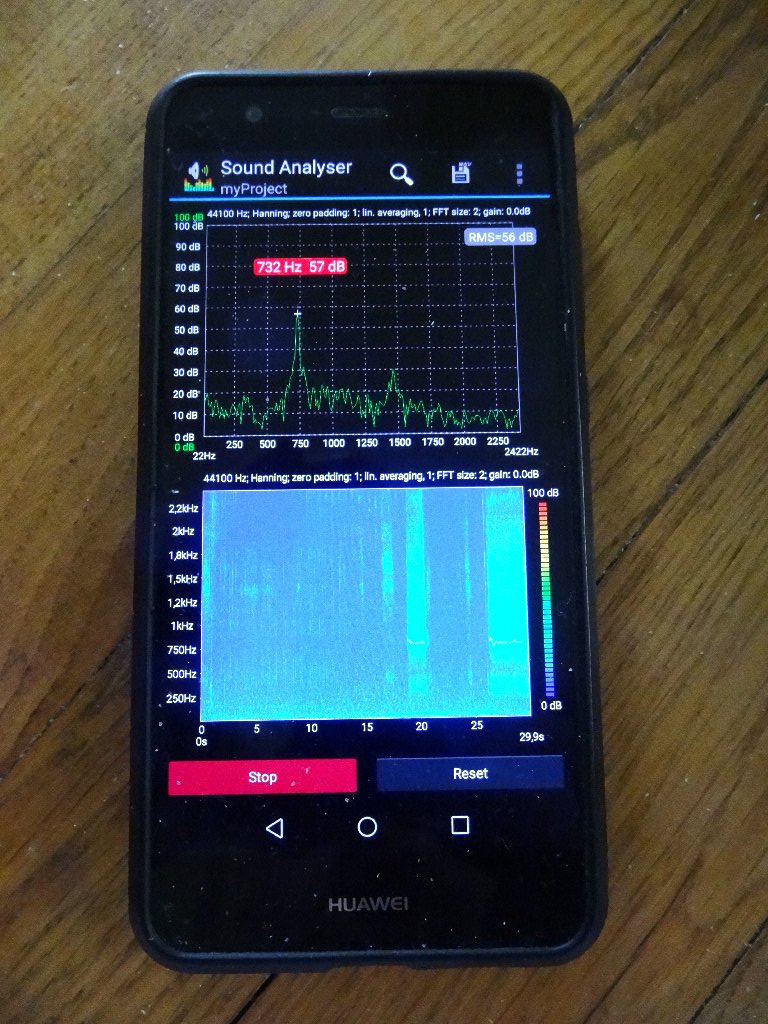

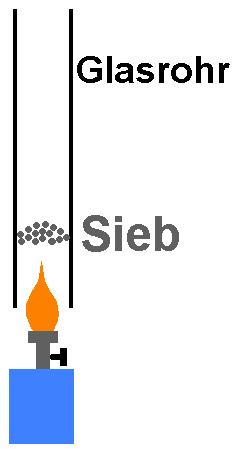


Hier das Frequenzspektrum für die kurze bzw. längere Röhre mit den jeweiligen Frequenzen des Grundtons bzw. der Obertöne:
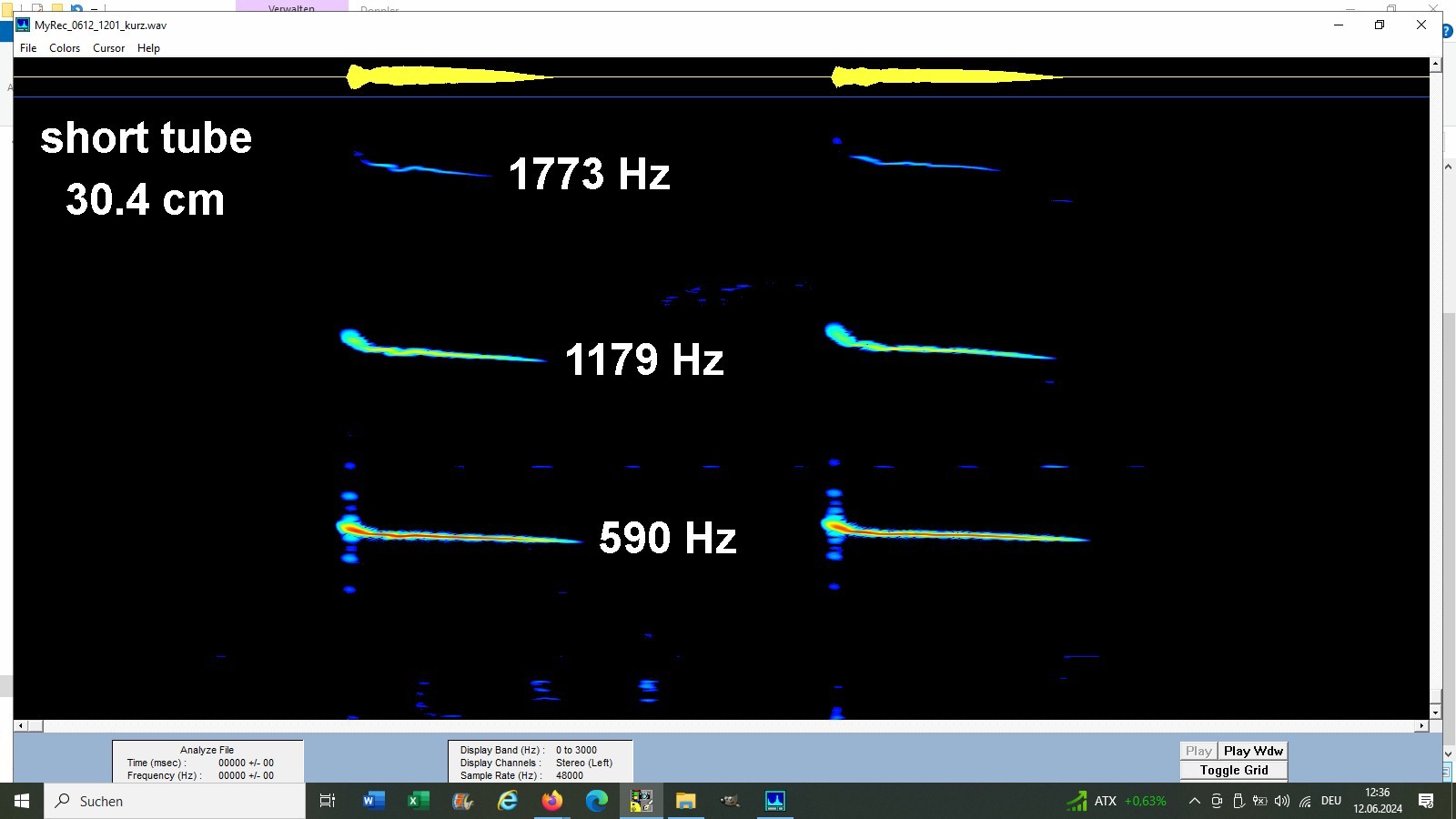
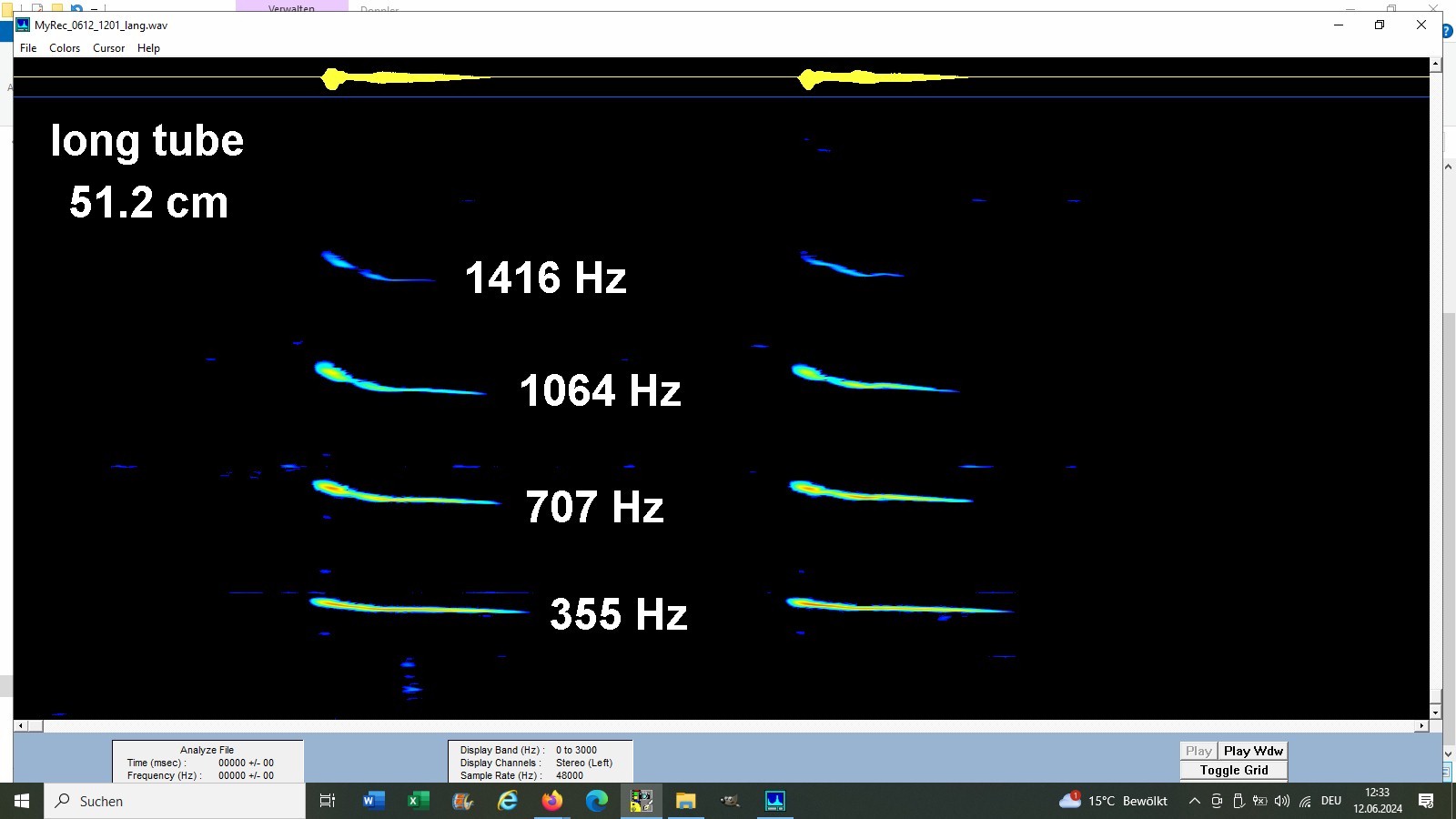
Für die Bestimmung der Schallgeschwindigkeit benötigt man z.B. die Frequenz f des Grundtons und die Länge der Glasröhre. In meinem Fall waren diese 30.4 cm bzw. 51.2 cm lang:



Durch die warme, aufsteigende Luft wird die Luftsäule zu Schwingungen angeregt und es entsteht eine sog. stehende Welle. Bei einem beidseitig geöffneten Rohr besitzt die stehende Wellen an beiden Enden einen Schwingungsbauch. Für die abgebildete Grundschwingung (dies ist jene Schwingung mit der geringsten Frequenz, welche die Randbedingungen erfüllt) gilt der Zusammenhang: λ = 2 · L.
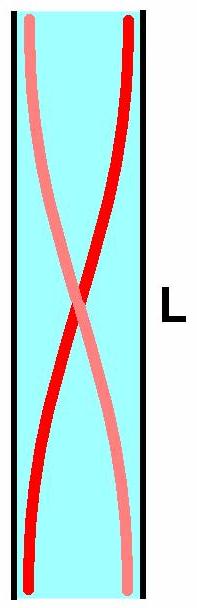
Weiters gilt die Wellengleichung c = λ · f. Nun kennen wir durch die Beziehung λ = 2 · L die Wellenlänge und die Frequenz f wurde ja mittels Handyapp oder einer anderen Software für den Computer ermittelt. Eingesetzt ergibt sich also für die Schallgeschwindigkeit: c = 2 · L · f

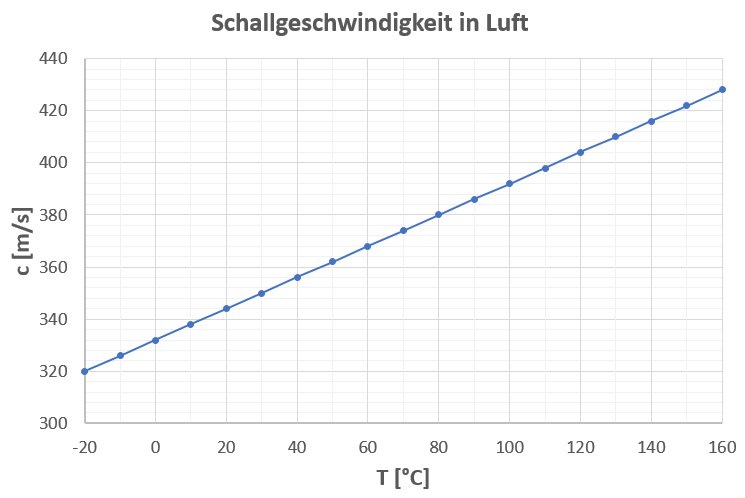
Da die Luft im Rohr durch den Bunsenbrenner erhitzt wurde, stimmt die berechnete Schallgeschwindigkeit nicht mit den bekannten Werten (3 sek für 1 km, also ca. 333 m/s) überein. Bei einer höheren Temperatur ist die Schallgeschwindigkeit nämlich größer:
Zum Abschluss noch das Youtube-Video:
Variante 3
Die Schallgeschwindigkeit c lässt sich auch mittels der Resonanzmethode nach Quincke ermitteln. Dazu wird eine Stimmgabel, ein längeres Plexiglasrohr, Schläuche, eine Plastikflasche und Wasser benötigt.

Bildquelle: https://commons.wikimedia.org/wiki/Category:Georg_Hermann_Quincke?uselang=de#/media/File:Georg_quincke.jpg/2, public domain
Die Stimmgabel und das Plexiglasrohr (Anm.: Ich werde zwei rund 30 cm lange Rohre miteinander verkleben) habe ich auf Temu besorgt:
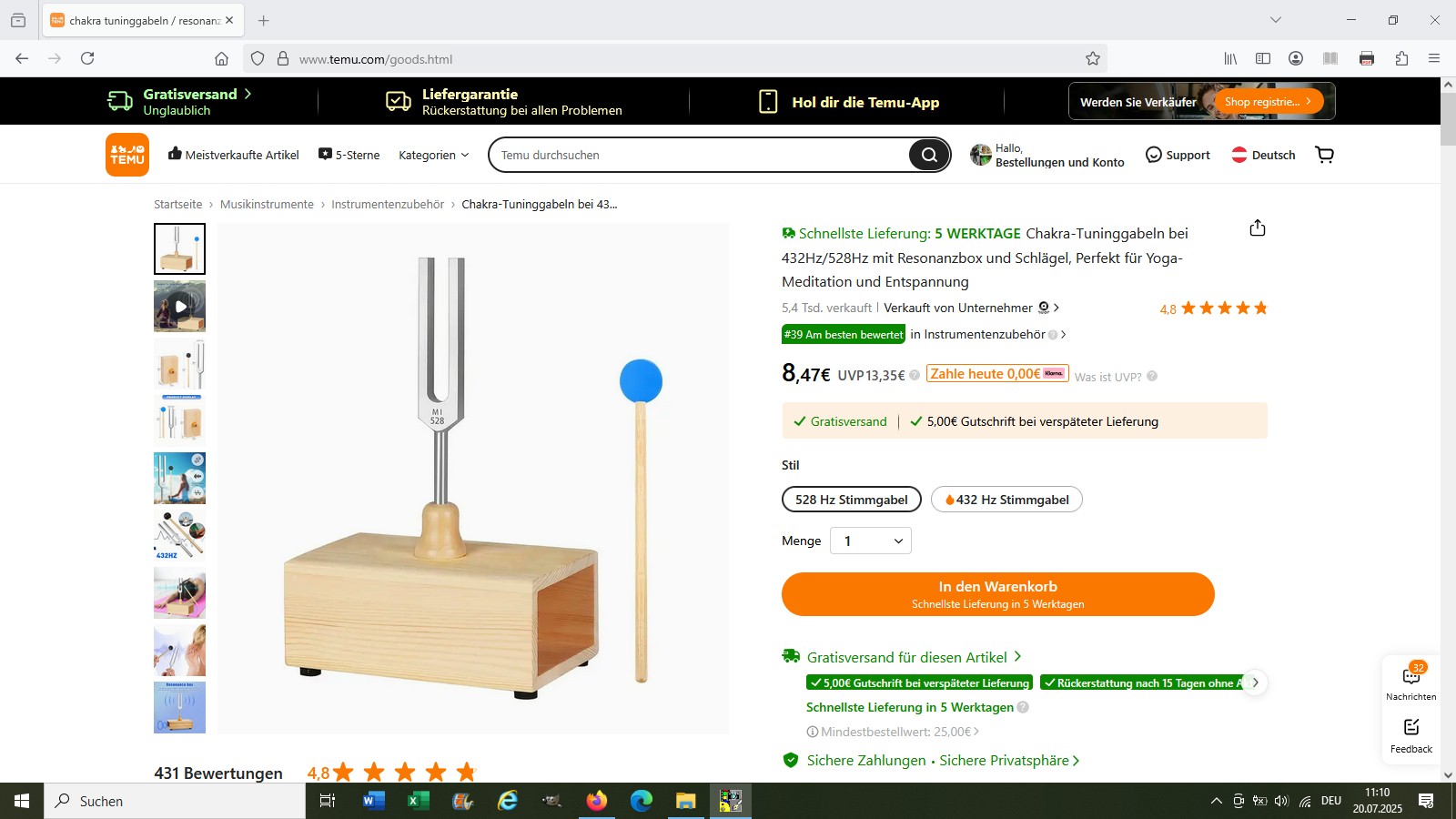

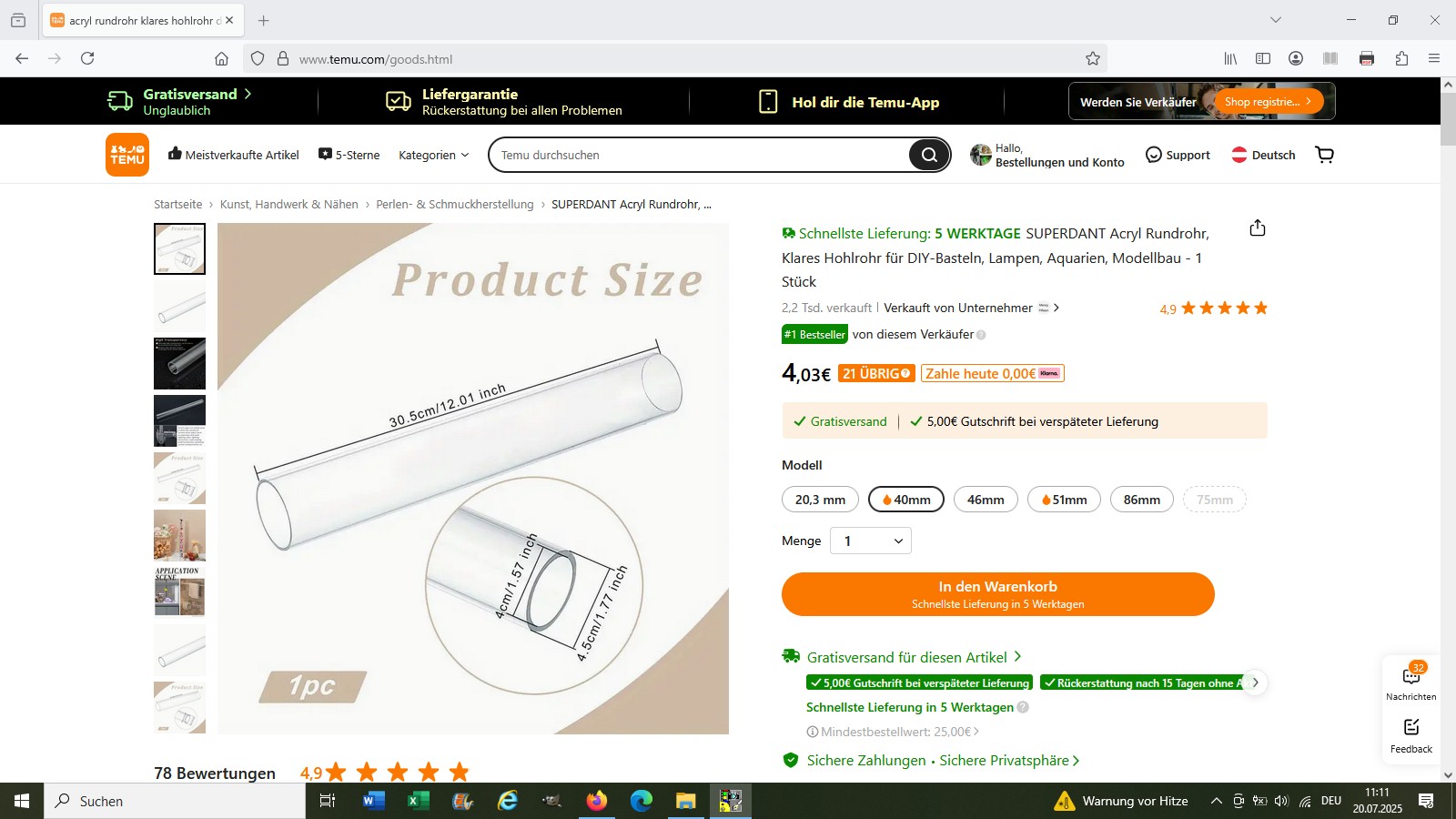




Der untere Boden mit eingeklebten Schlauchanschluss:

Zum Experiment selbst: Die Stimmgabel mit der Frequenz f wird am oberen Ende des Plexiglasrohrs fixiert. Das Rohr ist über einen Schlauch mit einem Wasserreservoire verbunden und teilweise mit Wasser gefüllt. Zuerst ist das Plexiglasrohr fast vollständig mit Wasser gefüllt. Man regt die Stimmgabel an und lauscht mit dem Rohr, wann die oberhalb des Wassers befindliche Luftsäule in Resonanz gerät. Dazu wird der Wasserspiegel im Plexiglasrohr immer weiter gesenkt.
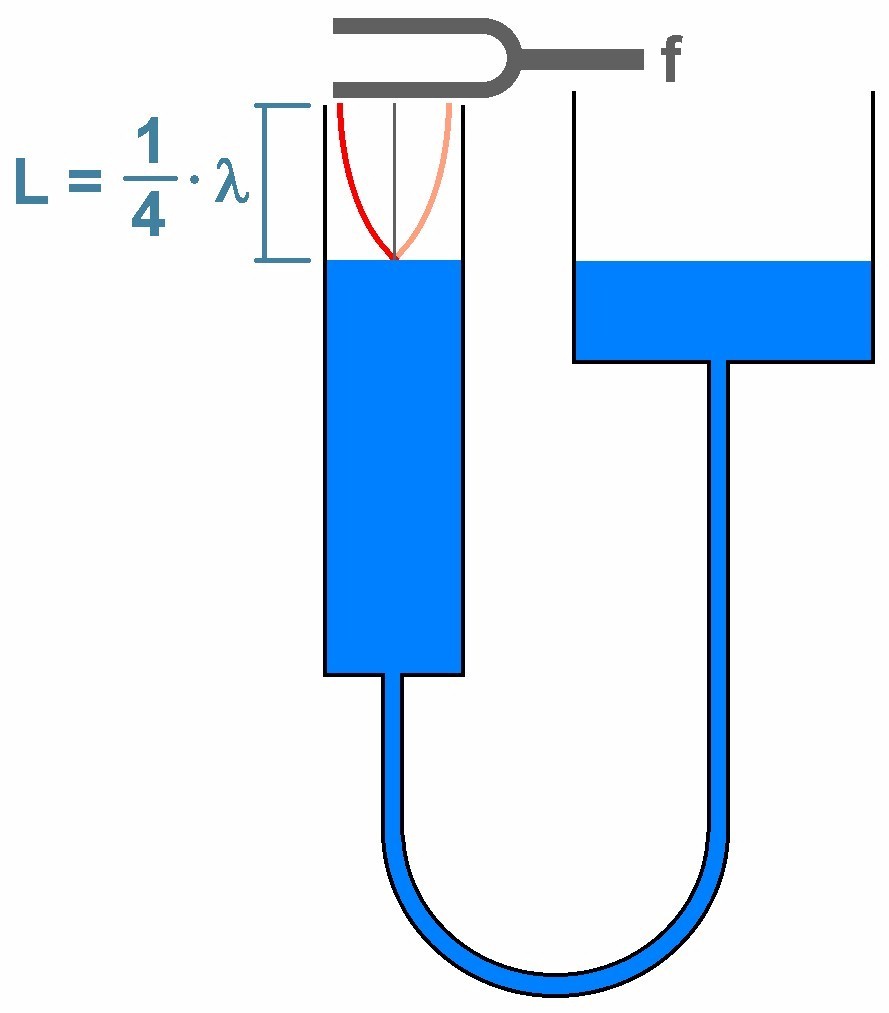
Die erste Resonanz erzielt man bei einer Luftsäulenlänge L = λ/4. Die erzeugte stehende Welle besitzt am Ort der Stimmgabel einen Bauch und am Ort der Wasseroberfläche einen Knoten (= Reflexion am festen Ende). Senkt man den Wasserspiegel weiter, so erhält man bei L = 3/4 · λ eine weitere Resonanz und der Stimmgabelton müsste lauter erklingen:
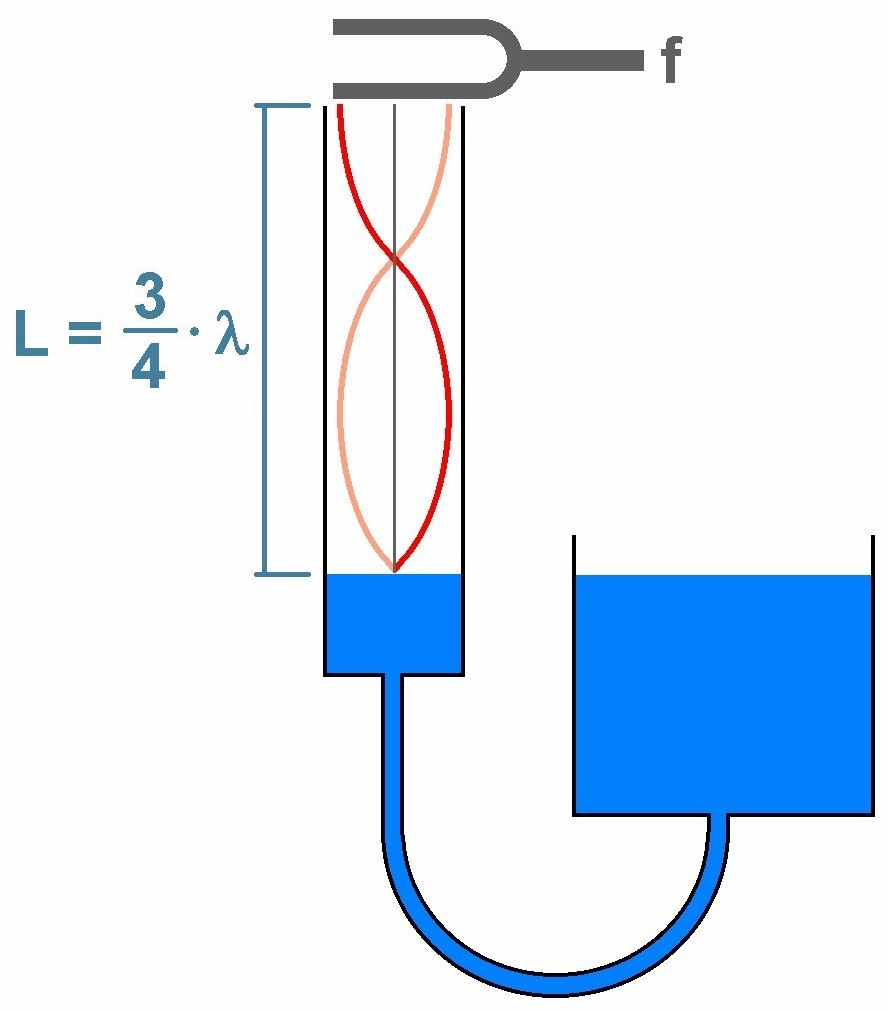
Kennt man nun die Längen L1 = 1/4 · λ und L2 = 3/4 · λ, so kann man daraus am besten über den Mittelwert die Schallwellenlänge λ bestimmen. Mittels der bekannten Frequenz f der Stimmgabel und der Wellengleichung c = λ · f ergibt sich dann daraus die Schallgeschwindigkeit c.
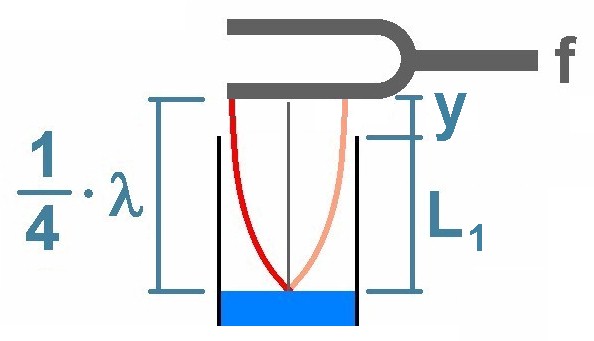
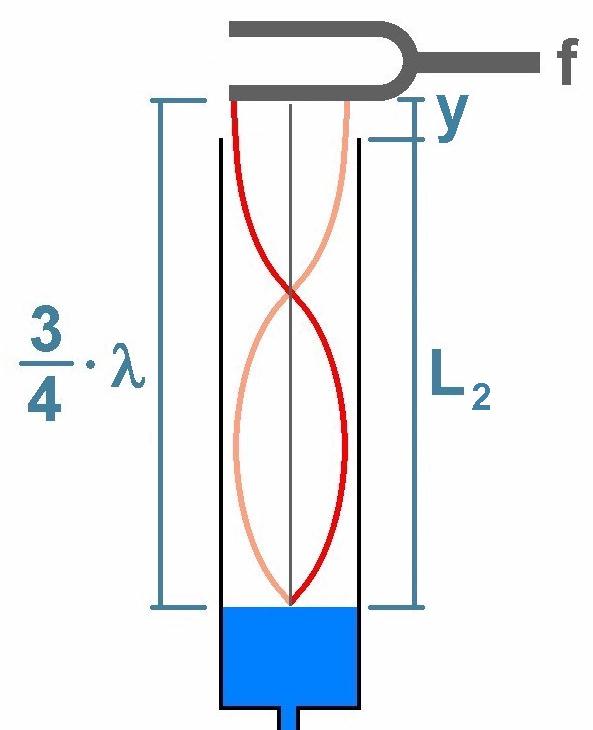
Will man die Schallgeschwindigkeit noch genauer ermitteln muss man berücksichtigen, dass die Stimmgabel nicht ganz bündig mit dem oberen Ende des Plexiglasrohrs abschließt. Es gilt daher L1 + y = 1/4 · λ und L2 + y = 3/4 · λ. Dies ist ein Gleichungssystem mit 2 Gleichungen und 2 Unbekannten y und λ. Eliminiert man y durch Subtraktion der beiden Gleichungen erhält man die Beziehung L2 + y – (L1 + y) = L2 – L1 = 3/4 · λ – 1/4 · λ = 1/2 · λ bzw. schlussendlich λ = 2 · (L2 – L1).

Anstelle eines Ausgleichsbehälters habe ich nun einfach das Plexiglasrohr bis zum oberen Rand mit Wasser gefüllt. Dann stoße ich die Stimmgabel an und messe mit einer Smartphone-App die Lautstärke. Im nächsten Schritt lasse ich Wasser über ein Ventil abfließen und bestimme bei der neuen Höhe abermals die Lautstärke. Dies wiederhole ich für mehrere Füllstände.


Hier sieht man gut die oberhalb der Öffnung postierte Stimmgabel und daneben das Handy zur Messung der Lautstärke:

Zur leichteren Bestimmung der Füllhöhe habe ich ans Plexiglasrohr Zentimetermarkierungen gezeichnet:

Die verwendete Lautstärken-App:
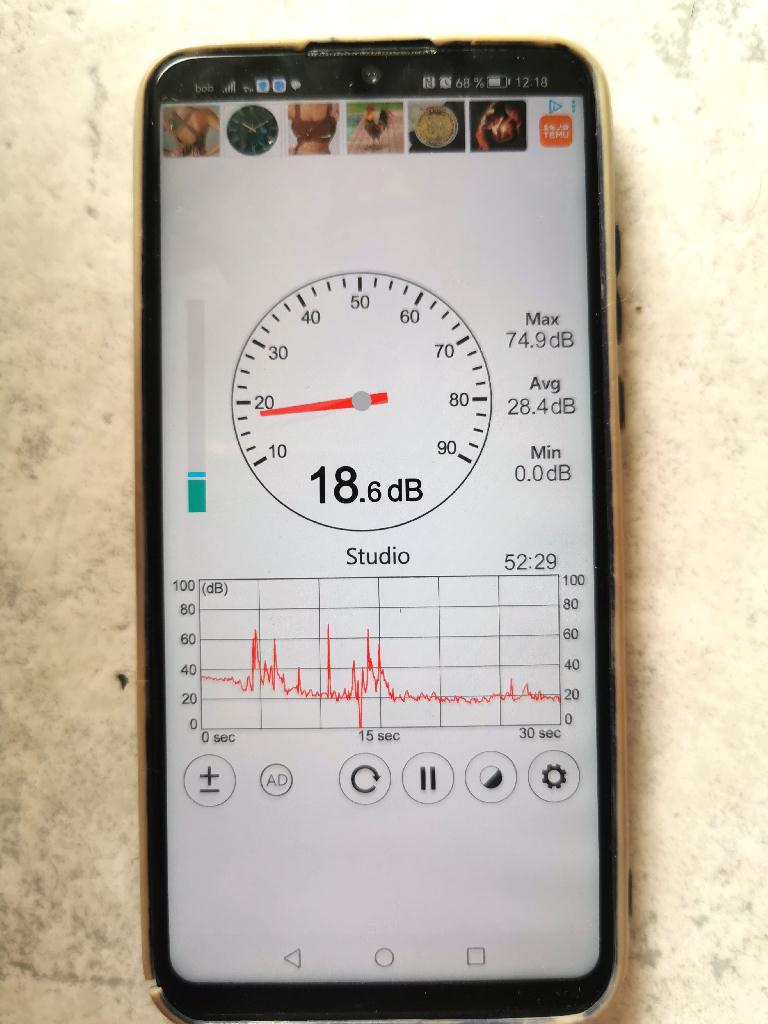
Wie erhofft erhalte ich an zwei Stellen eine deutlich erhöhte Lautstärke:
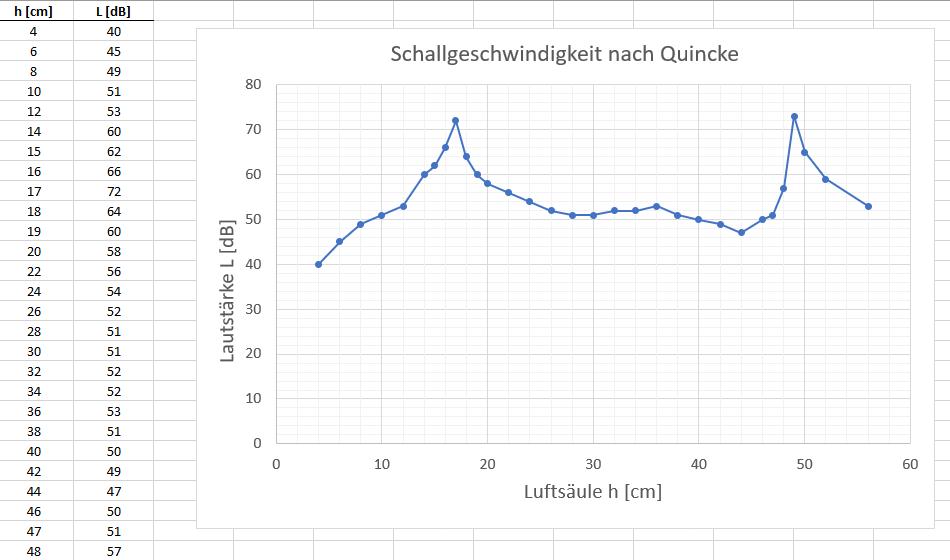
Der Abstand der beiden Maxima beträgt exakt eine halbe Wellenlänge, konkret 32 cm:
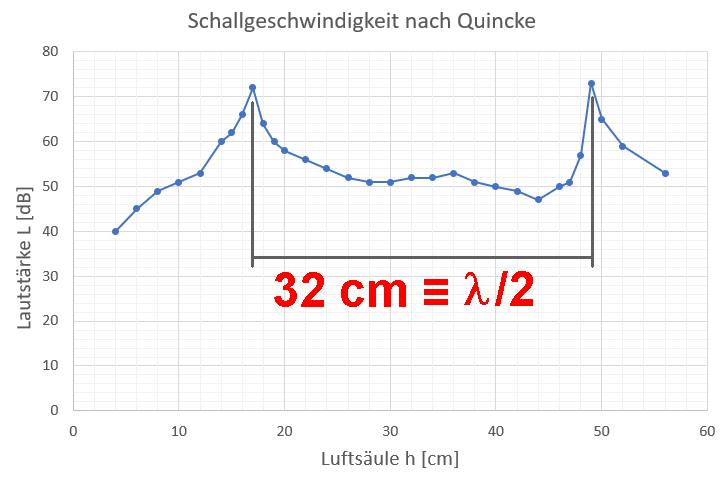
Jetzt kenne ich die Wellenlänge λ = 64 cm und die Frequenz der Stimmgabel f = 528 Hz. Mittels der Wellengleichung c = λ · f kann ich dann ganz einfach die Schallgeschwindigkeit berechnen. Mein Wert von c = 338 m/s ist sehr plausibel, Heureka 😉


