Der Ramsauer-Effekt, auch als Ramsauer-Townsend-Effekt bekannt, bezeichnet die extreme Durchlässigkeit von Gasen gegenüber langsamen Elektronen und wurde vom deutschen Physiker Carl Ramsauer (1879 – 1955) im Jahr 1920 entdeckt. Er gilt heute als der erste experimentelle Hinweis darauf, dass auch freie Elektronen nicht mit klassischer Mechanik beschreibbar sind.
Der ebenfalls für diesen Effekt verwendete Name Ramsauer-Townsend-Effekt schließt die Forschungen des irischen Physikers John Sealy Edward Townsend (1868 – 1957) ein, der 1901 die Abhängigkeit der mittleren freien Weglänge von der kinetischen Energie bei der Bewegung freier Elektronen in Gasen entdeckt hatte.
Basis quantenmechanischer Berechnungen ist die berühmte Schrödingergleichung. Dabei handelt es sich um eine Differentialgleichung mit der gesuchten Wellenfunktion ψ(r,t). Die zeitunabhängige Schrödingergleichung für die gesuchte Wellenfunktion ψ(r) lautet:
Dabei ist E die Energie des Elektrons und V(x) die potentielle Energie am Ort x. Nehmen wir an, dass Potential V(x) eines Atoms bestünde vereinfacht aus einem sog. Potentialtopf der Form
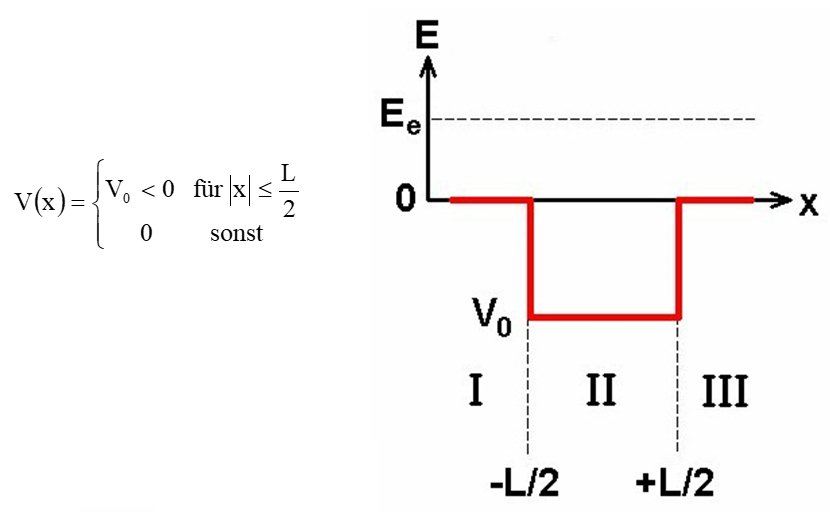
Wir setzen für die Lösungsfunktion ψ(r) folgende Ausdrücke an:
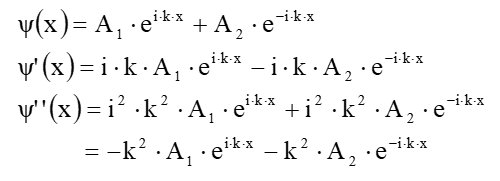
Setzt man die Ausdrücke für ψ(r) bzw. ψ“(r) in die Schrödingergleichung ein, erhält man:


Jetzt muss man nur noch dafür sorgen, dass die 3 Wellenfunktionen und deren Ableitungen an den Übergangspunkten bei x = -L/2 und x = +L/2 stetig sind.

Was wir nun wissen wollen ist die Wahrscheinlichkeit dafür, dass das Elektron sich im Bereich III nach rechts weiter bewegt.

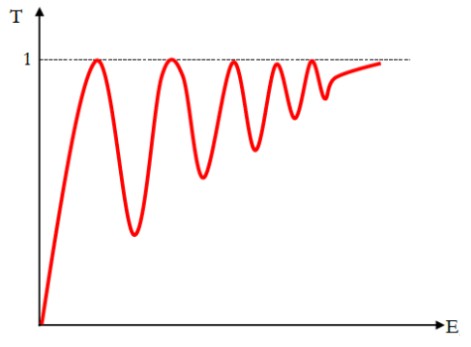
Wie man sieht, hängt diese Transmissionswahrscheinlichtkeit T neben dem Parameter ρ entscheidend vom Faktor sin²(κ · L) ab. Ist dieser Ausdruck 0, wird die Transmissionswahrscheinlichkeit T = 1 ≡ 100%.
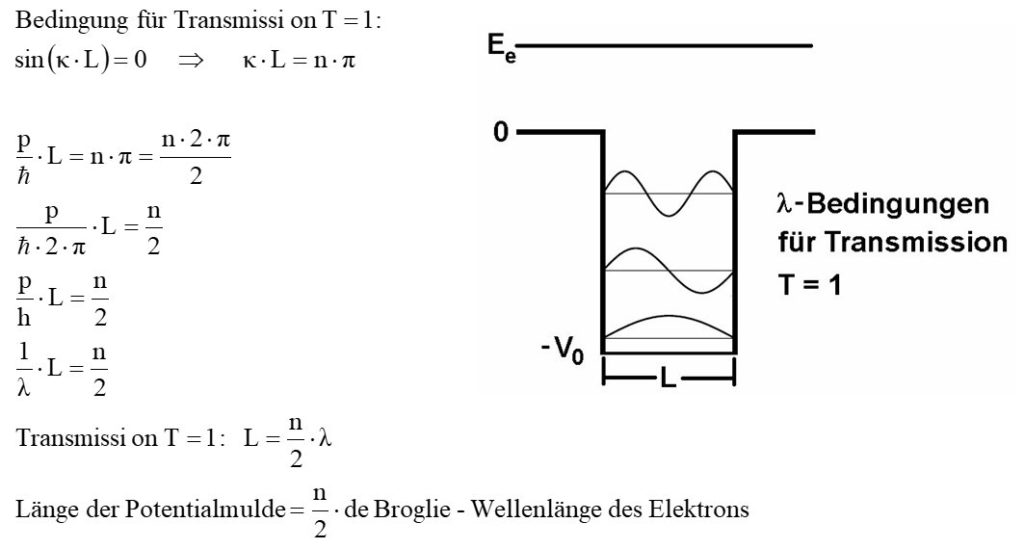
Die Transmissionswahrscheinlichkeit T wird also immer dann maximal bzw. gleich 1, wenn die die Länge L des Potentialtopfs ein ganzzahliges Vielfaches der halben de Broglie Wellenlänge λ/2 des Elektrons ist!
Wie lässt sich das nun experimentell überprüfen? Nun man benötigt für den Ramsauer-Townsend-Effekt eigentlich nur eine Elektronenröhre vom Typ 2D21. Diese erhält man günstig etwa auf ebay.
Man legt nun eine steigende Spannung an die Anode und misst jeweils den Anoden- bzw. Shield-Strom. Mit steigender Beschleunigungsspannung U steigt auch die kinetische Energie der Elektronen, da ja E = U·e gilt. Steigende kinetische Energie E bedeutet aber auch einen größeren Impuls p der Elektronen. Und ein größeres p bewirkt nach der bekannten Welle-Teilchen-Beziehung von de Broglie λ = h/p eine kleinere Wellenlänge λ. Mit zunehmenden U sinkt also die Wellenlänge λ der Elektronen.
Der Anodenstrom muss nach den obigen Herleitungen immer dann maximal werden (Anm.: Dies ist dann gleichbedeutend mit einer maximalen Transmissionswahrscheinlichkeit T), wenn der Atomdurchmesser L ein ganzzahliges Vielfaches der halben de Broglie Wellenlänge des Elektrons ist.
Für das erste Anodenstrommaximum muss also gelten: 1 · λ/2 = Atomdurchmesser L
Für das zweite Anodenstrommaximum bei höherer Spannung U demnach 2 · λ/2 = Atomdurchmesser L
usw.
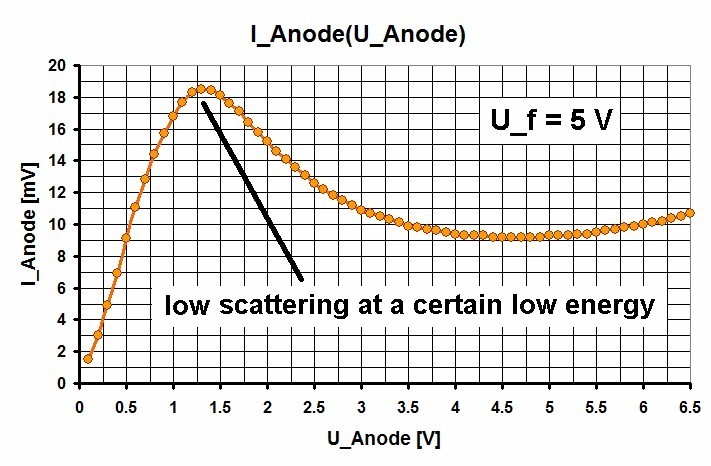
Und genau diese Beobachtung macht man in meinem Experiment. Der Anodenstrom steigt zu Beginn mit wachsender Beschleunigungsspannung U an, um bei U ≈ 1.25 V ein erstes Maximum zu besitzen. Danach sinkt der Anodenstrom wieder ab, um bei höherem U neuerlich ein Maximum zu besitzen.
Wie wir wissen, gilt für das erste Strommaximum: 1 · λ/2 = Atomdurchmesser L
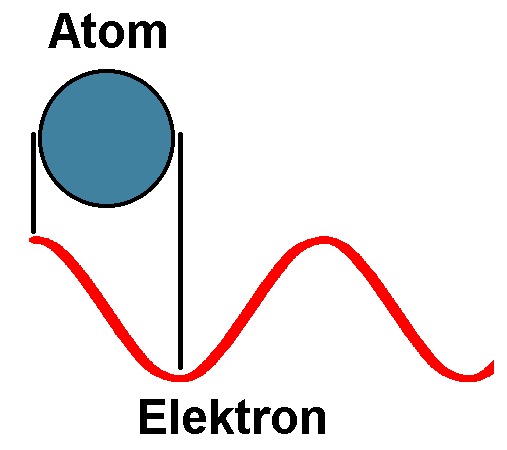
Kennen wir für diesen Fall die Beschleunigungsspannung U (konkret 1.25 V), so kann man wiefolgt die Wellenlänge λ berechnen:
Ekin = m · v² / 2 = p² / 2 · m = U · e
Für den Impuls p des Elektrons folgt daraus:
p = √(2 · m · U · e) = √(2 · 9.1 · 10^ –31 · 1.25 · 1.6 · 10^ –19) ≈ 6 · 10^ –25 kg·m/s
Setzt man diesen Wert für p in die de Broglie Beziehung ein, erhält man für die Wellenlänge λ des Elektrons:
λ = h / p = 6.63 · 10^ –34 / (6 · 10^ –25) = 1.1 · 10^ –9 m
Da ja in diesem Fall Atomdurchmesser L = λ/2 gilt, folgt schlussendlich für den Atomdurchmesser
L = 5.5 · 10^ –10 m
Dieser Wert ist durchaus plausibel.



Der einfache Schaltplan:
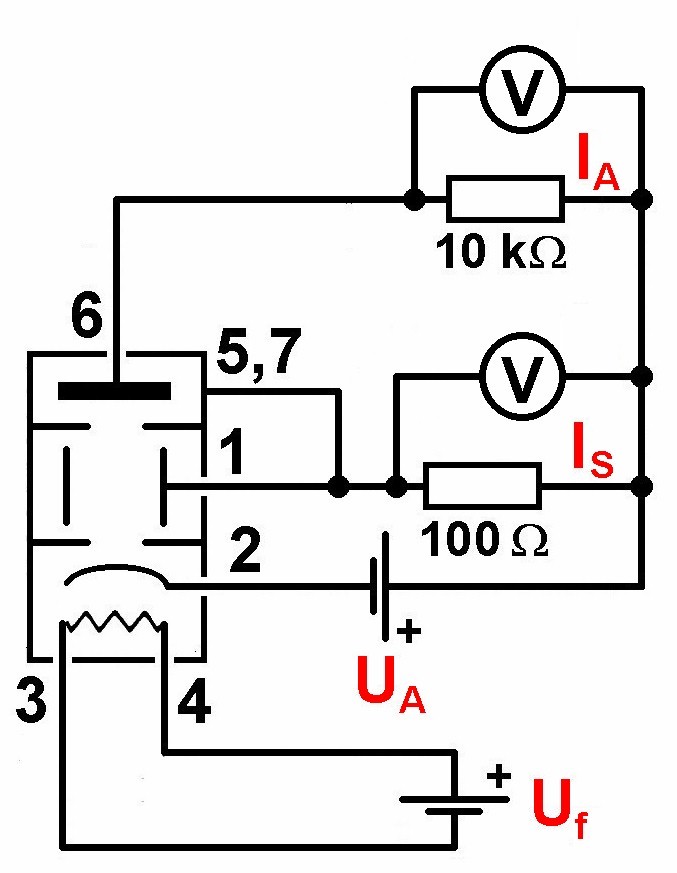
Der Anodenstrom IA bzw. Shield-Strom IS wird über den Spannungsabfall am 10 kOhm- bzw. 100 Ohm-Widerstand ermittelt! Die Heizspannung Uf der Röhre beträgt rund 4.8 V.