Unter einem mathematischen Pendel versteht man eine Punktmasse m, die an einem masselosen Faden der Länge L aufgehängt ist und frei schwingen kann. Die Periodendauer τ dieser Schwingung hängt nur von der Fadenlänge L ab, wenn man die Erdbeschleunigung g als gegeben annimmt. Es gilt konkret:

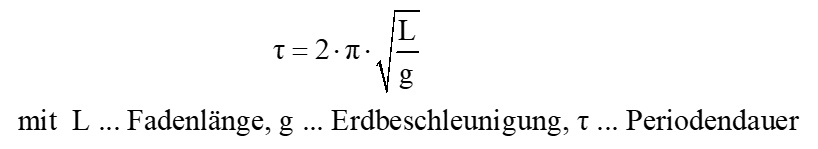
Das mathematische Pendel ist eine Idealisierung. Reale Gegebenheiten berücksichtigt das sog. physikalische Pendel. Hierbei handelt es sich um einen beliebigen Körper, welcher auf einer Achse aufgehängt ist und ebenfalls frei schwingt. Für dessen Periodendauer gilt die etwas andere Formel

 

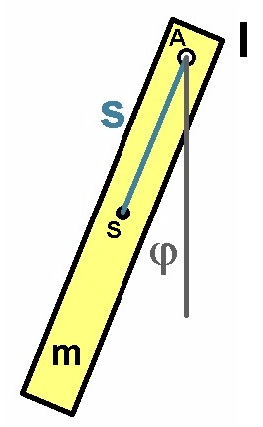
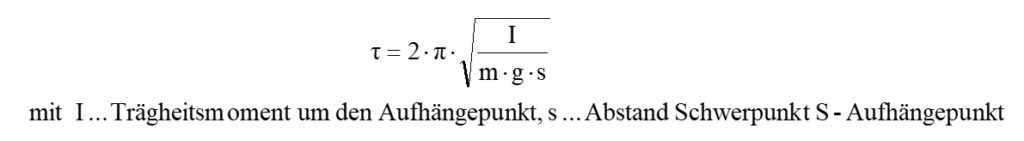
In dieser Formel kommt das Trägheitsmoment I um den Aufhängepunkt A, die Masse des Pendels und der Abstand s vom Schwerpunkt S zum Aufhängepunkt A vor. Das mathematische Pendel ist ein Spezialfall des physikalischen Pendels, denn es gilt dann mit der Fadenlänge L: I = m · L² und s = L. Daraus folgt wieder die Formel für das mathematische Pendel 2·π·√L/g.

Die Herleitung für diese Formel ist nicht kompliziert:

Für ein schönes Experiment zum physikalischen Pendel benötigt man nur eine Holzleiste mit 19 Löchern der Firma Matador (https://www.matador.at/Produkte/Explorer-5/Einzelteile-Ersatzteile/Streben/19er-Streben::72.html) und eine Achse für die Schwingung.

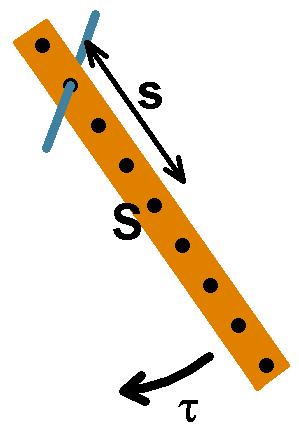
Der Schwerpunkt S der Holzleiste befindet sich genau in der Mitte beim 10ten Loch. Nun hängt man die Holzleiste bei verschiedenen Löchern auf und bestimmt jeweils die Periodendauer τ in Abhängigkeit vom Abstand s des Aufhängepunkts A zum Schwerpunkt S. Die Messung wiederholt man für alle 9 bzw. 10 Löcher. Hängt man nämlich die Holzleite genau im Schwerpunkt, also im 10ten Loch auf, so schwingt diese gar nicht mehr und die Periodendauer geht ins Unendliche. Der Abstand zwischen zwei benachbarten Löchern beträgt genau 2 cm, sodass der Abstand s zwischen 0 und 18 cm betragen kann. Hier nun die Messergebnisse:

 

Der Graph besitzt bei einem bestimmten s-Wert ein Minimum. Warum ist dies so? Nun, für das Trägheitsmoment I um den Aufhängepunkt A gilt der Satz von Steiner:

Setzt man diesen Ausdruck in die Formel für die Periodendauer ein und bestimmt mittels Differentialrechnung das Extremum, so erhält man:

Konkret beträgt der Abstand s für das Minimum der Periodendauer s = 11.4 cm. Dieses theoretische Ergebnis deckt sich sehr gut mit dem Experiment (siehe Graph oben). Hierfür hat man die Masse m und das Trägheitsmoment I_S um den Schwerpunkt eingesetzt.

Beide Werte m und I_S lassen sich einfach bestimmen. Für die Masse benötigt man nur eine Waage und das Trägheitsmoment um den Schwerpunkt S kann man mittels der gewonnenen Periodendauern ermitteln. Angenommen die Periodendauer beträgt für s = 18 cm genau 1.01 Sekunden. Setzt man diese Werte in die Formel ein, erhält man für das Trägheitsmoment I um den gewählten Aufhängepunkt:

Wir wollen aber das Trägheitsmoment I_S um den Schwerpunkt S wissen. Hierfür verwendet man wieder den Satz von Steiner:

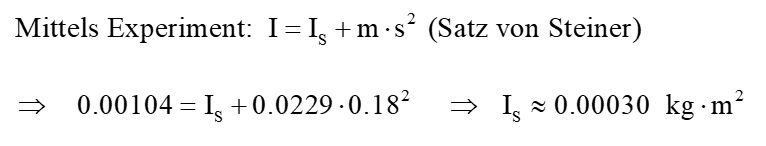
Das Trägheitsmoment I_S um den Schwerpunkt beträgt also 0.00030 kg·m². Es lässt sich aber auch theoretisch ermitteln, da die Holzleiste ja einem Quader der Länge L = 38 cm und der Masse m = 0.0229 kg entspricht. Für diese Geometrie gibt es bereits eine fertige Formel für I_S:

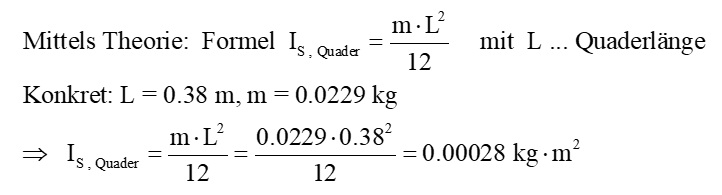
Wie man sieht, differieren experimenteller und theoretischer Wert nicht allzu viel. Das Youtube-Video reiche ich natürlich wie gewohnt nach.