Ein Monochord ist ein sehr simples Saiteninstrument mit nur einer einzigen Saite zur Untersuchung der Schwingungsfrequenz in Abhängigkeit einiger Parameter wie Saitenlänge oder Saitenspannung. Gestoßen bin ich auf dieses Projekt beim Schmökern im Katalog der Firma Leybold/LD-Didactic: https://www.leybold-shop.com/vp1-7-2-1.html
Die für dieses Experiment im Falle eines Selbstbaus benötigten Teile erhält man bei Amazon bzw. im örtlichen Baumarkt (Holzleiste, Aluwinkel).







Ich möchte ja auch die Schwingungsfrequenz in Abhängigkeit von der Spannkraft F untersuchen. Aus diesem Grund habe ich auch eine günstige Federwaage mit einer Anzeige von 0 bis 15 kg (also ca. 0 bis 150 N) erworben:


Hier die Umlenkrolle für die Saite:


Meine Küche habe ich wieder wie gewohnt kurzerhand in eine Werkstatt umfunktioniert 😉

Der Querschnitt des Holzbalkens beträgt 10 x 6 cm.

Die Montierung des Stimmwirbels:


Der Steg gebastelt aus einem 30 x 20 mm Aluwinkel:


So sieht es des öfteren in meiner Küche aus:


Die kleine, gefeilte Mulde im Steg zur Fixierung der Saite:



Das fertige Monochord:

Wie ich die Schwingungsfrequenz am besten bestimme, muss ich mir noch überlegen.
So, die Entscheidung ist gefallen. Ich werde die Schwingungsfrequenz der Saite mit einer Lichtschranke bestimmen. Zur Anwendung kommt dabei ein Arduino-Näherungsmodul.
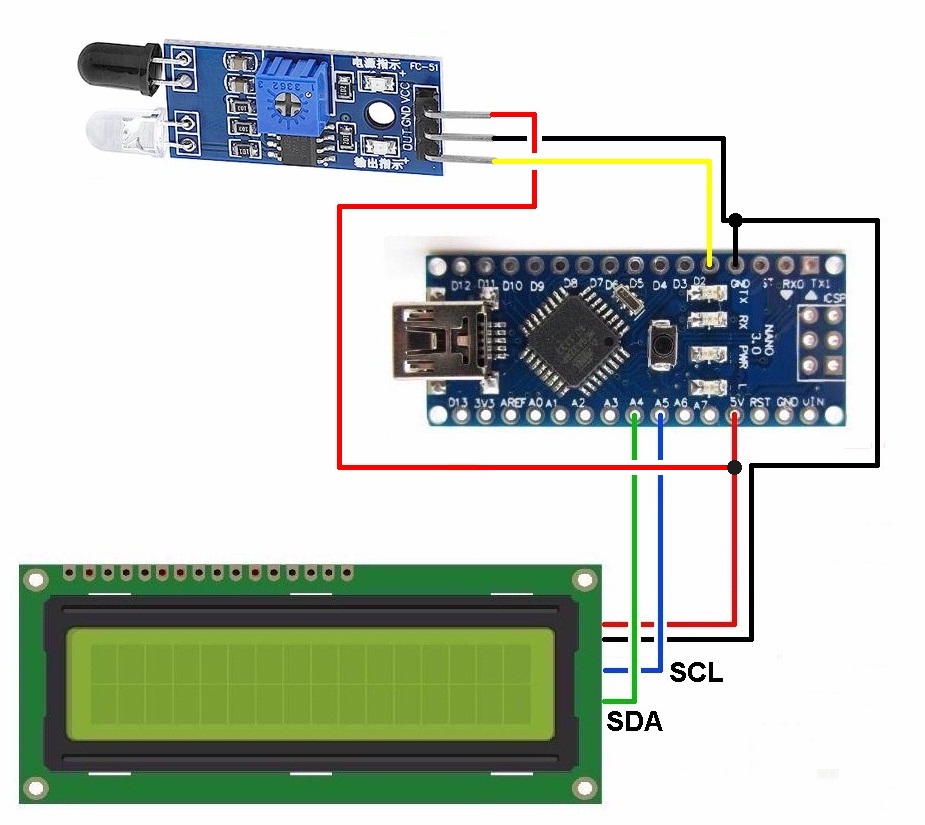

Damit dieses auch auf den roten Laser anspricht, habe ich die IR-Photodiode ausgelötet und gegen eine auch für den sichtbaren Spektralbereich geeignete Photodiode ausgetauscht.

Meine Photodiode ist im Bereich 400 nm bis 1100 nm sensibel:


Hier sieht man, wie die Photodiode am Modul verlötet werden muss:

Der gesamte Messaufbau:






Die Messergebnisse: Bei einer Spannkraft von F = 2 kg (ca. 20 N) betrug die Schwingungsfrequenz 33.45 Hz.


Bei einer Spannkraft von F = 10 kg stieg die Frequenz auf 80.3 Hz:


Und schließlich bei F = 12 kg betrug f = 88.2 Hz:


Die Wellengeschwindigkeit c in der Saite ist proportional zur Wurzel aus der Spannkraft F. Mit der Wellengleichung c = λ · f folgt dann für die Schwingungsfrequenz f bei gleichbleibender Wellenlänge λ bzw. Saitenlänge = λ/2:
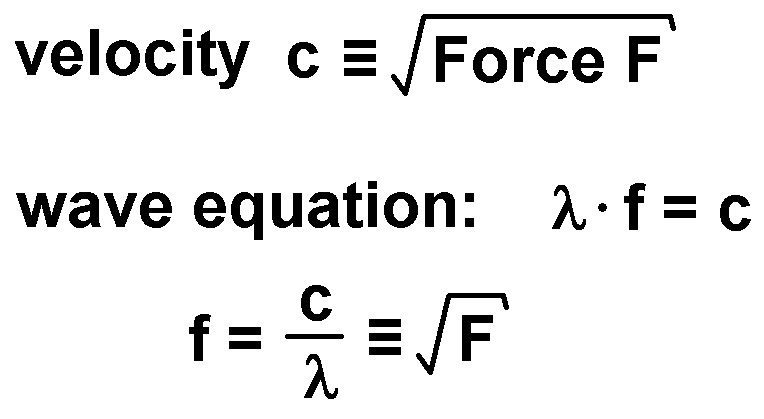
Trägt man also f² gegen die Spannkraft F auf, so müsste man eine ansteigende Gerade erhalten:
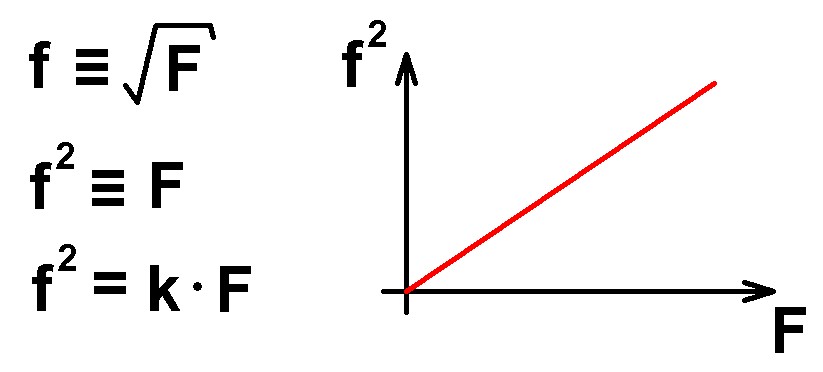
Genau dies war der Fall, wie meine experimentellen Messwerte zeigen:
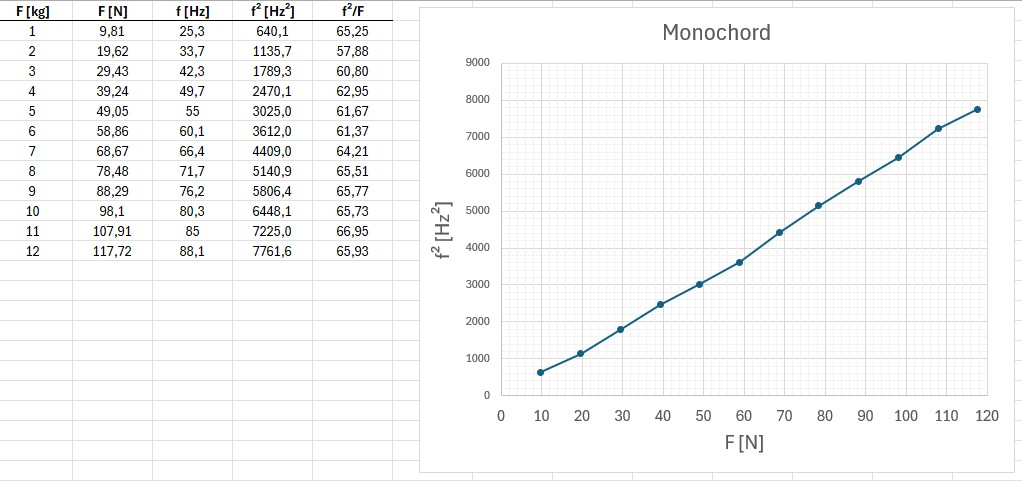
Da bleibt mir wieder einmal nur zu sagen, Heureka 😉
Zum Schluss noch der einfache Arduino-Code für den Frequenzmesser:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
#include <LiquidCrystal_I2C.h> #include <Wire.h> LiquidCrystal_I2C lcd(0x27,16,2); // set the LCD address to 0x27 for a 16 chars and 2 line display. ACHTUNG: Adresse kann auch 0x3F sein !!! // Anschlüsse: // GND - GND // VCC - 5V // SDA - ANALOG Pin 4 // SCL - ANALOG pin 5 int sensor = 2; unsigned long currentTime; unsigned long lastTime; //unsigned long pulse_freq; unsigned long period; float pulse_freq; // =========================== // ======= SETUP ========= // =========================== void setup() { pinMode(sensor, INPUT); Serial.begin(9600); attachInterrupt(digitalPinToInterrupt(sensor), pulse, FALLING); // Setup Interrupt lcd.begin(); // initialize the lcd lcd.backlight(); lcd.setCursor(0,0); lcd.print("Drehzahl-"); lcd.setCursor(0,1); lcd.print("messer"); delay(3000); lcd.setCursor(0,0); lcd.print(" "); lcd.setCursor(0,1); lcd.print(" "); lastTime = micros(); } // ======================== // ======= LOOP ========= // ======================== void loop () { pulse_freq = 1000000.0 / period; lcd.setCursor(0,0); lcd.print("f = "); lcd.print(pulse_freq, 2); lcd.print(" Hz "); lcd.setCursor(0,1); lcd.print(pulse_freq * 60, 0); lcd.print(" RPM "); } // ============================= // ======= INTERRUPT ========= // ============================= void pulse () // Interrupt function { currentTime = micros(); period = currentTime - lastTime; lastTime = currentTime; } |
Wie immer zum Schluss das Youtube-Video:

