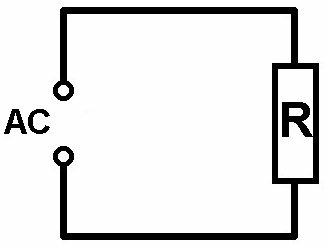
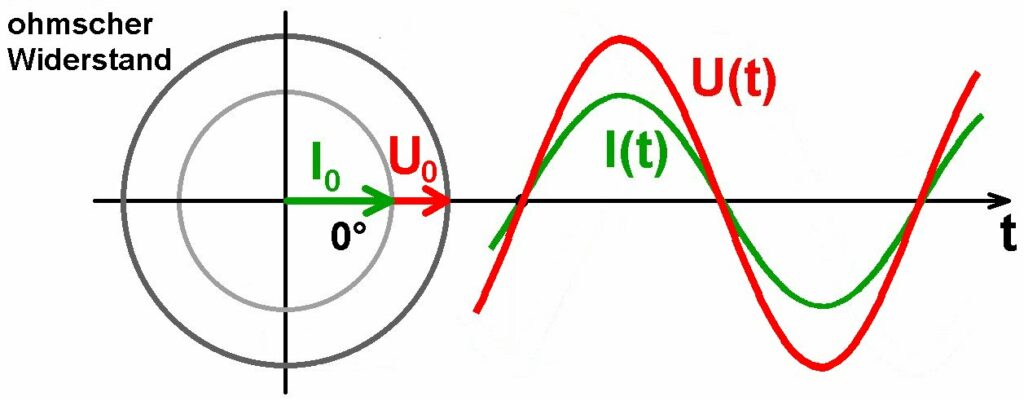
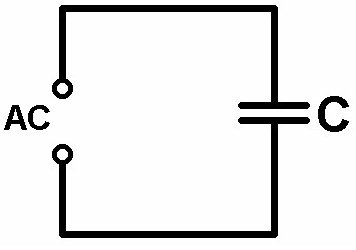
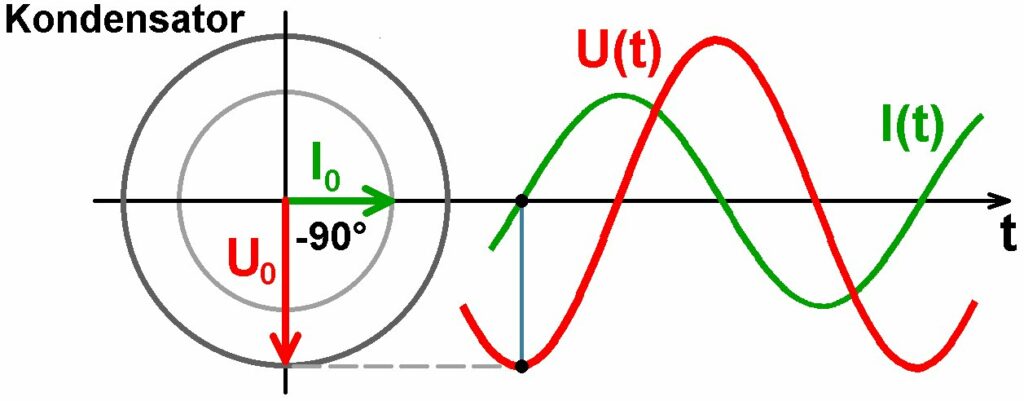
Schließt man an eine Wechselspannung einen Kondensator oder eine Induktivität, so sind Strom und Spannung nicht mehr phasengleich sondern gegenseitig verschoben. Der Grund dafür ist, dass beim Kondensator der Strom der Spannung um eine Viertelperiode (≡ 90° oder π/2) vorauseilt und bei einer Induktivität die Spannung um 90° dem Strom. Nur bei einem ohmschen Widerstand sind Spannung und Stromstärke phasengleich!

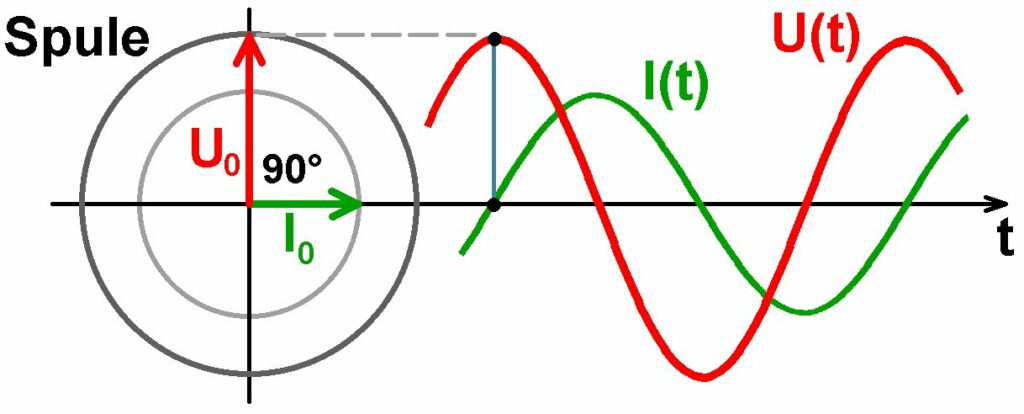
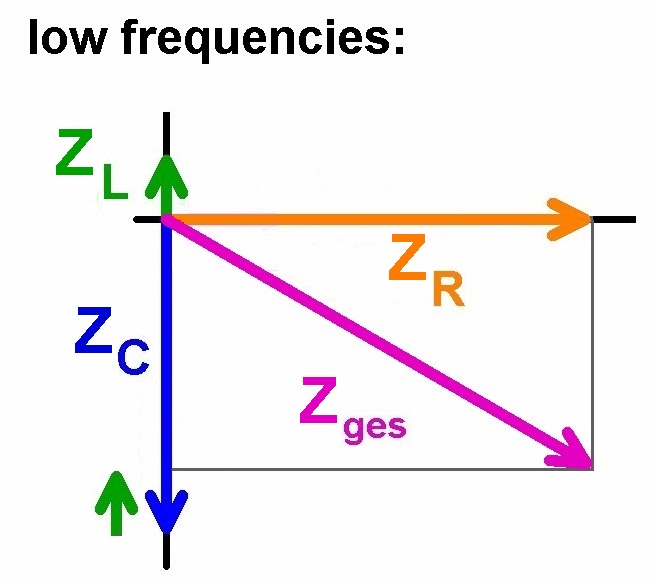
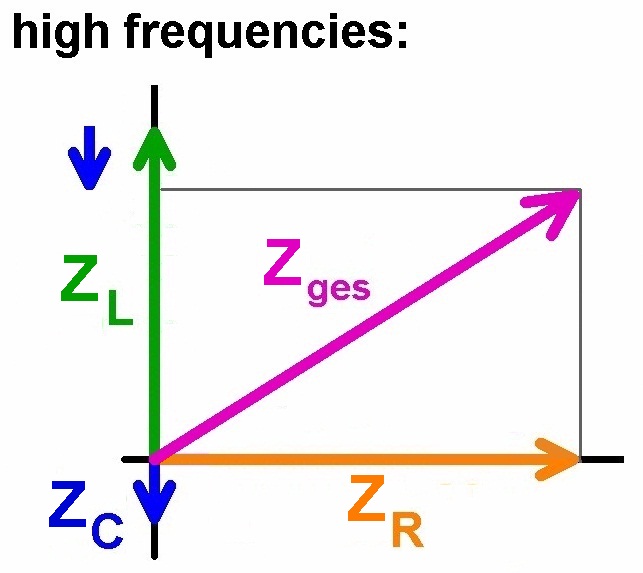
Bei einer Serienschaltung von einem ohmschen Widerstand R, einer Kapazität C und einer Induktivität L fließt durch alle 3 Bauteile der gleiche Strom I. Die einzelnen Spannungen U_R , U_C und U_L weisen aber wie eben schon angesprochen eine Phasenverschiebung von 0°, -90° und + 90° auf. Im Zeigerdiagramm ist dies einfach darzustellen.

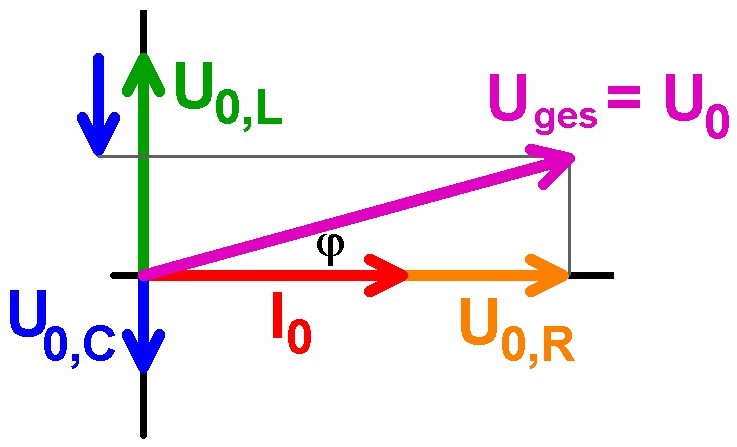
Die vektorielle Summe der 3 Einzelspannungen muss aber natürlich wieder die Gesamtspannung U₀ der Spannungsquelle ergeben. Es muss also gelten:

Da durch alle drei Bauteile derselbe Strom I₀ fließt, erhält man nach Division durch I₀ den folgenden Ausdruck für die Impedanz der Serienschaltung:

Für die Impedanzen Z, also dem Verhältnis aus Spannungsamplitude U₀ und Stromamplitude I₀, gelten folgende einfache Beziehungen: Für einen ohmschen Widerstand ist Z_R = R, für eine Induktivität Z_L = ω·L und für eine Kapazität Z_C = 1 / (ω·C). Setzt man dies in die obige Formel für Z_ges ein, erhält man den Serienwiderstand von R, L und C:

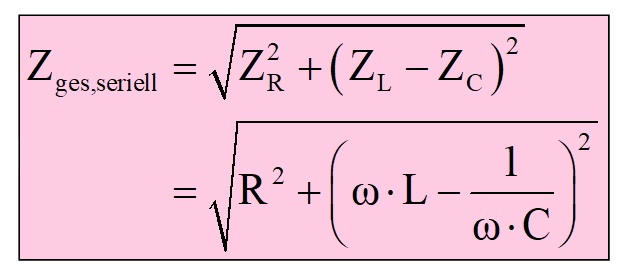
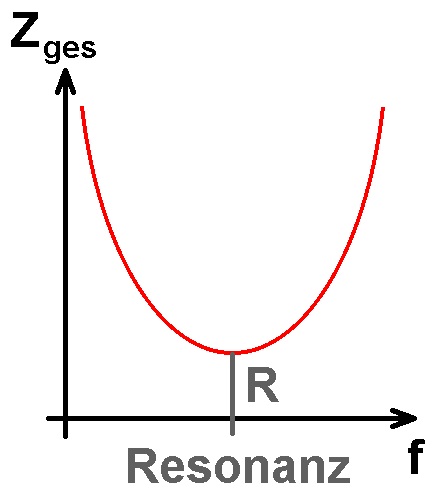
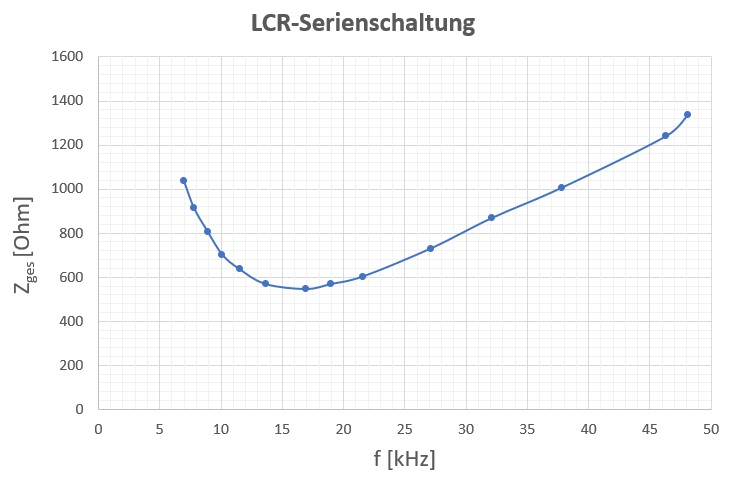
Trägt man Z_ges gegen die Frequenz f auf, so bemerkt man, dass bei einer bestimmten Resonanzfrequenz der Gesamtwiderstand/die Gesamtimpedanz minimal ist. Dies ist dann der Fall, wenn sich die Teilimpedanzen Z_L und Z_C gerade kompensieren. Es gilt dann: Z_ges = minimal = R, also nur noch der reine ohmsche Widerstand.

Aus der Forderung Z_L = Z_C für die Resonanz, kann die Resonanzfrequenz sehr einfach hergeleitet werden. Es gilt für sie:

Für L = 10 mH und C = 10 nF beträgt die Resonanzfrequenz konkret 15.92 kHz. Dies werden wir gleich experimentell überprüfen. Hierfür baue ich folgende einfache Schaltung auf:

Mit dem Oszilloskop verfolge ich den Spannungsverlauf U_R am ohmschen Widerstand. Mit dem ohmschen Gesetz I = U/R kann daraus sehr leicht der Stromverlauf ermittelt werden. Die Spannung am Widerstand und die Stromstärke besitzen bei rund 16 kHz tatsächlich ein Maximum.

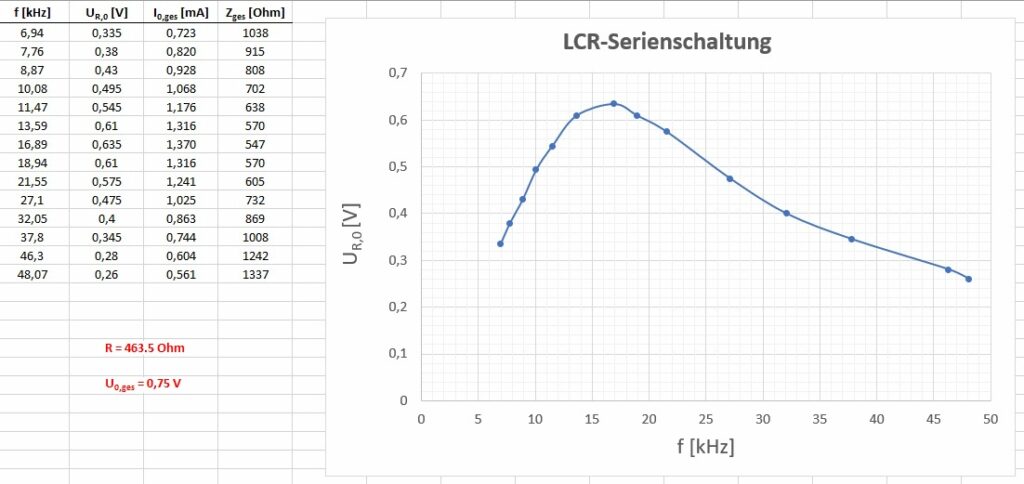
Kennt man den Gesamtstromamplitude I_0,ges, so kann man daraus mit der Spannungsamplitude des Funktionsgenerators U_0,ges = 0.75 V sehr einfach die Gesamtimpedanz Z_ges = U_0,ges/I_0,ges berechnen. Diese besitzt wie zu erwarten war im Resonanzfall ein Minimum, voila.

Das Youtube-Video reiche ich wie immer nach…