Strahlt man mit einem Laser durch eine flüssige Probe, so wird der Laserstrahl mehr oder weniger abgeschwächt. Eine Rolle spielt dabei die Länge x der Probe und natürlich auch die Flüssigkeit selbst bzw. die Konzentration der Lösung. Die Lichtintensität wird dabei von I0 auf I abgeschwächt.
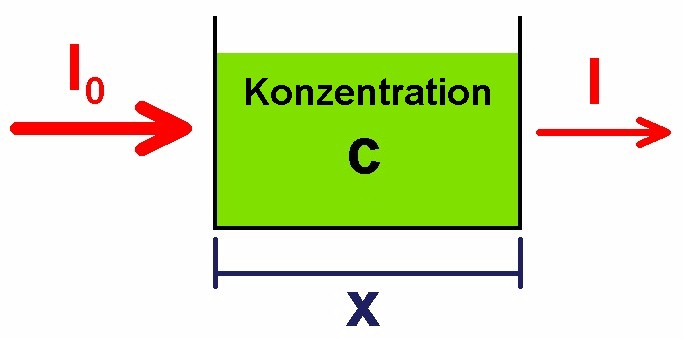
Betrachten wir die Intensitätsabnahme pro kurzem Längenstück, also dI/dx. Diese ist zuerst einmal sicher negativ. Dann ist diese wohl auch proportional zur Konzentration c der Lösung. Eine höher konzentrierte Lösung schwächt den Laserstrahl mit Sicherheit stärker. Und dann ist die Intensitätsabnahme auch noch proportional zur Intensität I selbst. Angenommen die Intensität nimmt nach 3 cm auf die Hälfte ab, also von I0 nach I0/2. Dann nimmt die Intensität auf weiteren 3 cm ebenfalls wieder um die Hälfte ab, also von I0/2 auf 0.5 · I0/2 = I0/4. Auf den ersten 3 cm hat also die Intensität absolut gesehen um I0/2 abgenommen, auf den zweiten 3 cm aber nur noch um I0/4. Die Intensitätsabnahme ist sozusagen prozentuell, also relativ betrachtet immer gleich aber absolut gesehen nimmt sie ab! Der Intensitätsverlauf I(x) wird dann in etwa wiefolgt aussehen:
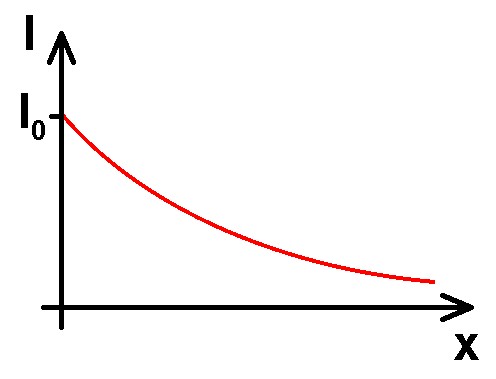
Leiten wir nun diese scheinbar prozentuelle bzw. exponentielle Abnahme mathematisch her:

Wir erhalten also das bekannte Lambert-Beersche-Gesetz, welchen nach den beiden Personen Johann Lambert (1728 – 1777) und August Beer (1825 – 1863) benannt ist.

Bildquelle: https://de.wikipedia.org/wiki/Datei:Johann_Heinrich_Lambert_1829_Engelmann.png, public domain
Die Lichtintensität I bestimme ich mit einer Photodiode. Dazu habe ich mir ein einfaches Gerät auf Basis eines Tranzimpedanzverstärkers (TIA) mit der Photodiode SFH203 gebastelt:
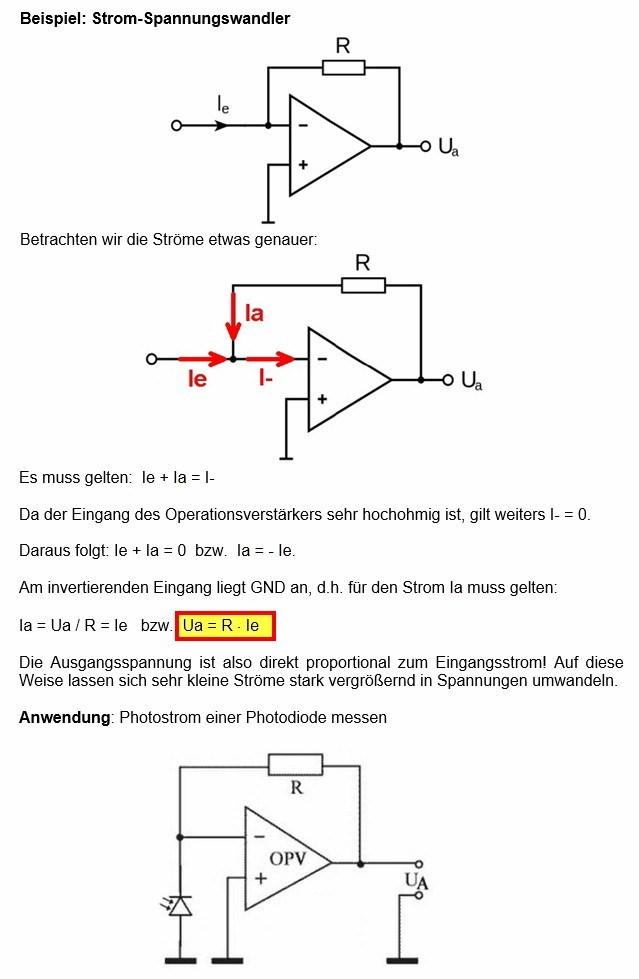
Die Ausgangsspannung ist also proportional zum Photostrom der Photodiode. Und dieser Photostrom ist proportional zur Lichtintensität I. Es gilt also U ≡ I. Der Schaltplan ist recht simpel:
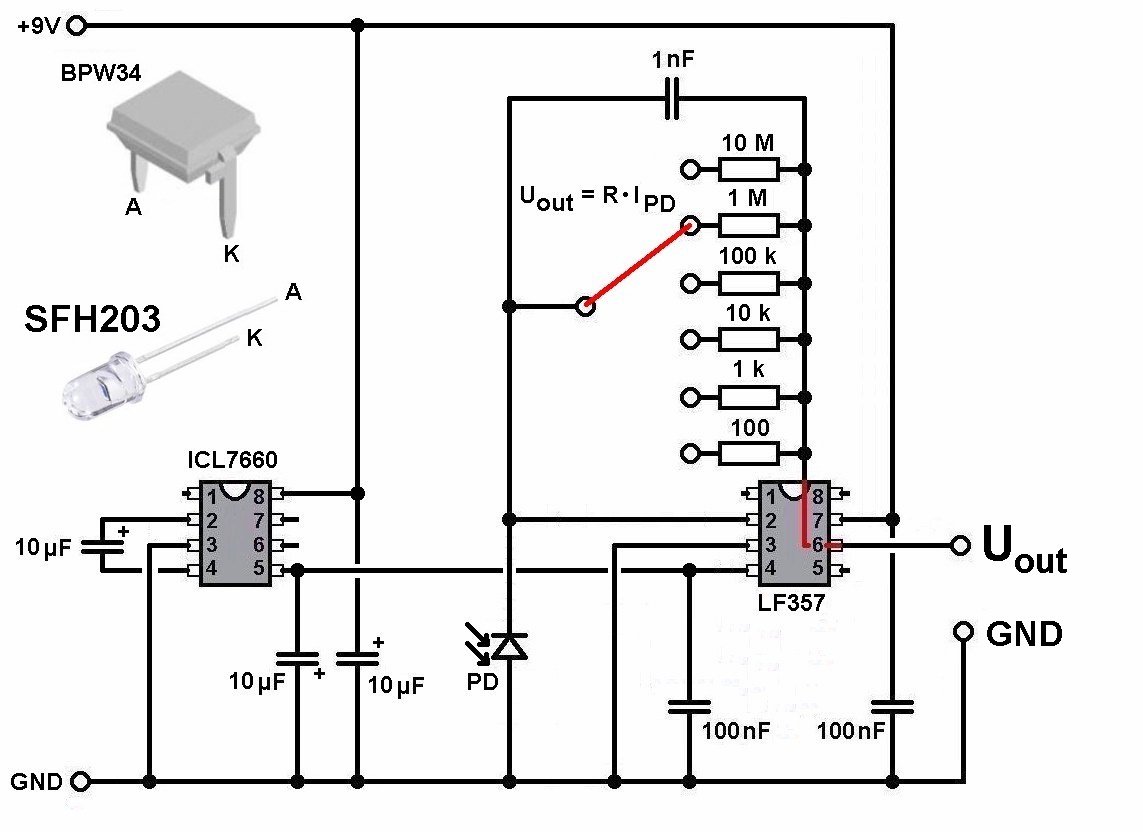






Mit dem Drehschalter verändere ich den Verstärkungsfaktor im Bereich von 10² bis 10^ 7.

Die zu Beginn abgebildete Skizze hat eine kleine praktische Unzulänglichkeit.

Wird die Konzentration c oder die Länge x gleich 0, so folgt nach dem Lambert-Beer-Gesetz: I = I0 · exp(–0) = I0 · 1 = I0, d.h. die Lichtintensität nimmt überhaupt nicht ab. In der Praxis ist dem natürlich nicht so, denn die Küvette selbst, auch wenn sie nur mit reinem Wasser gefüllt ist (c wäre in diesem Fall 0) oder ein lichtes Maß von x = 0 besäße, schwächt ja das Licht selbst auch bereits etwa durch Reflexionen an den Grenzschichten! Die Intensität I0 darf also nicht vor der Küvette gemessen werden, sondern nachher bei einer nur mit Wasser gefüllten Küvette.
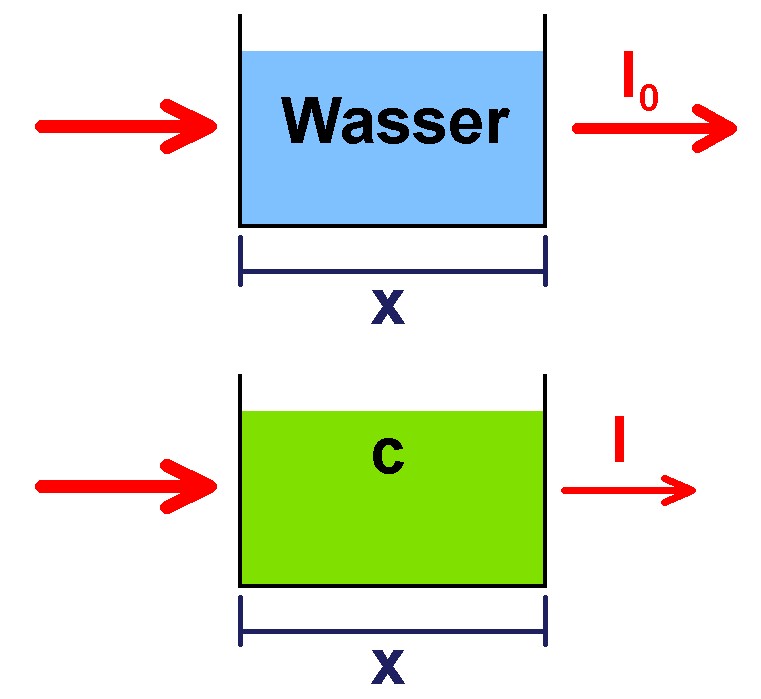
Hier also der schematische Aufbau/Ablauf des Versuchs:
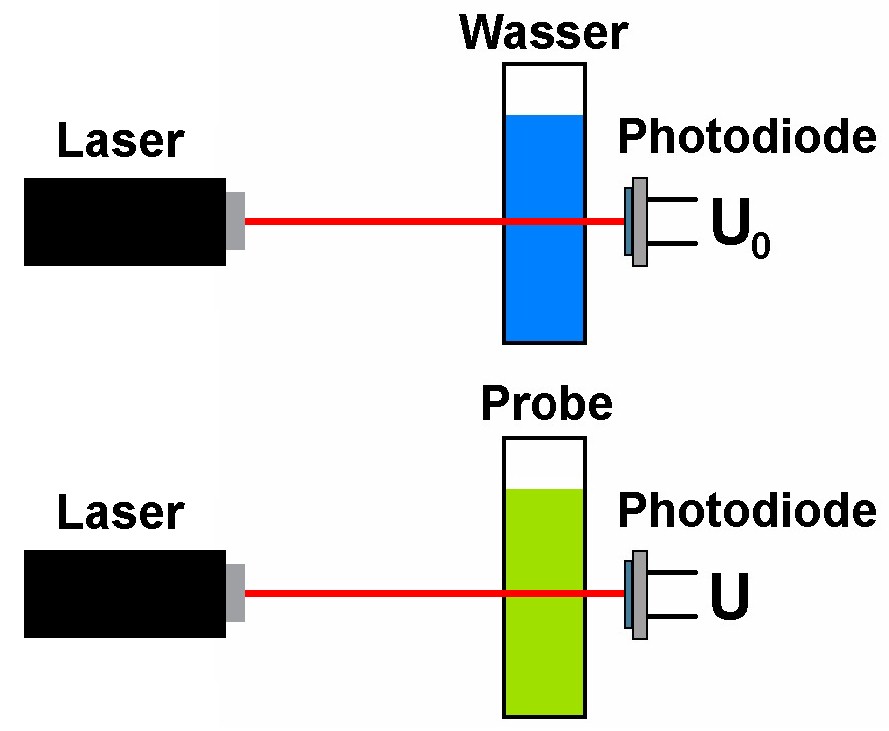
Die Abhängigkeit der Intensität I von der Strecke x untersuche ich mittels unterschiedlich langer Küvetten. Auf aliexpress habe ich ein günstiges Angebot entdeckt und Küvetten mit Längen zwischen x = 5 mm und 50 mm bestellt:
Wie man am Datums- und Zeitstempel rechts unten erkennt, habe ich selbst zu Silvester nichts besseres zu tun, als mich um meine Physikprojekte zu kümmern 😉


Dem Wasser werde ich entweder Kaliumpermanganat oder Methylenblau in unterschiedlichen Konzentrationen c zuführen. Beides habe ich übers Internet gekauft.


Betrachten wir noch einmal das Lambert-Beer-Gesetz:

Die neu eingeführte Größe Extinktion E ist ein aussagekräftiges Maß für die Intensitätsschwächung. Beträgt E etwa 1, so gilt I = I0 / 10, bei E = 2 wird die Intensität bereits auf 1/100 = 1/10² abgeschwächt und bei E = 3 gilt etwa I = I0 / 10³. Tragen wir die Extinktion E = lg(I0/I) gegen die Strecke x oder die Konzentration c auf, so müssten wir eine steigende Gerade erhalten:
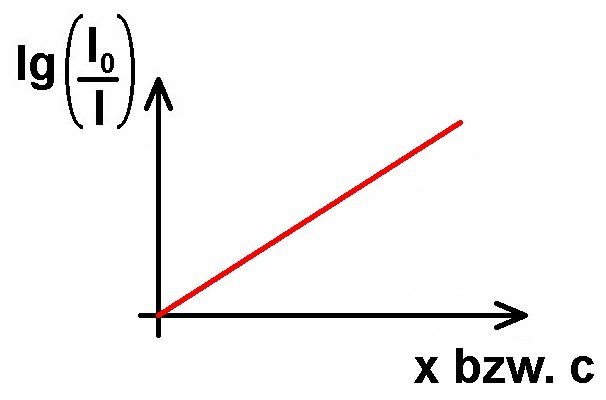
Genau dies werde ich experimentell überprüfen.
Variation der Länge x
Im ersten Teil des Experiments lasse ich die Konzentration c konstant und variiere die Länge x der Küvette.



Die Kaliumpermanganatlösung:


Länge x = 30 mm:


Länge x = 5 mm:


Zum Schluss musste noch die Spannung U0 für x = 0 bestimmt werden. Da ich aber keine Küvette der Länge 0 habe, verwendete ich die kürzeste mit x = 5 mm und füllte diese mit reinem Wasser.



Die Messergebnisse:
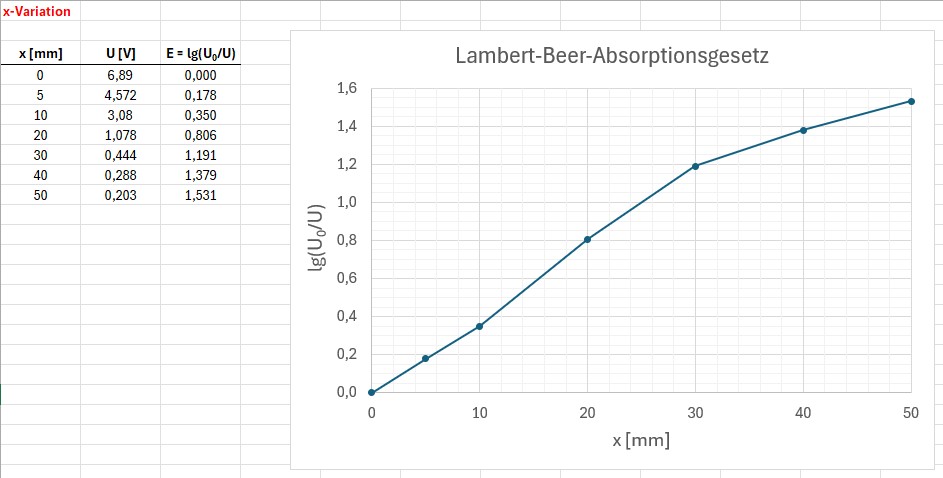
Wie man sieht, erhalte ich für Küvettenlängen bis ca. x = 30 mm einen schönen linearen Zusammenhang zwischen der Extinktion E = lg(U0/U) und der Länge x. Für größere Strecken stimmt dann das Lambert-Beer-Gesetz nicht mehr und die Kurve flacht ab.
Variation der Konzentration c
Im zweiten Teil des Versuchs bleibt nun die Länge x der Küvette unverändert und es verändert sich die Konzentration c. Dazu erzeuge ich zunächst eine große Startkonzentration c. Danach entferne ich mit der Pipette die Hälfte dieser Lösung und ersetze sie durch reines Wasser. Dies ergibt dann die Konzentration c · 0.5. Ersetze ich dann wieder die Hälfte der Lösung durch reines Wasser erhalte ich c · 0.5². Dieses Prozedere wiederhole ich immer wieder und erhalte allgemein c · 0.5^ n.
Für diese Vorgehensweise markierte ich mir ein Volumen V und V/2 an der 10 mm langen Küvette:

Die auf diese Weise erhaltenen Konzentrationen von c bis c · 0.5^ 13:

Die Startkonzentration c kannte ich aber quantitativ nicht. Von daher kann ich bei allen Konzentrationen nur willkürliche Einheiten (engl. arbitrary units oder kurz a.u.) angeben.




Hier betrug die Konzentration nur noch c · 0.5^ 9:


Auch für diesen Versuch musste ich wieder U0 bestimmen, was einer Konzentration c = 0 entspricht. Daher füllte ich zum Schluss die Küvette mit reinem Wasser:



Die erhaltenen Messergebnisse und der Graph E(c):
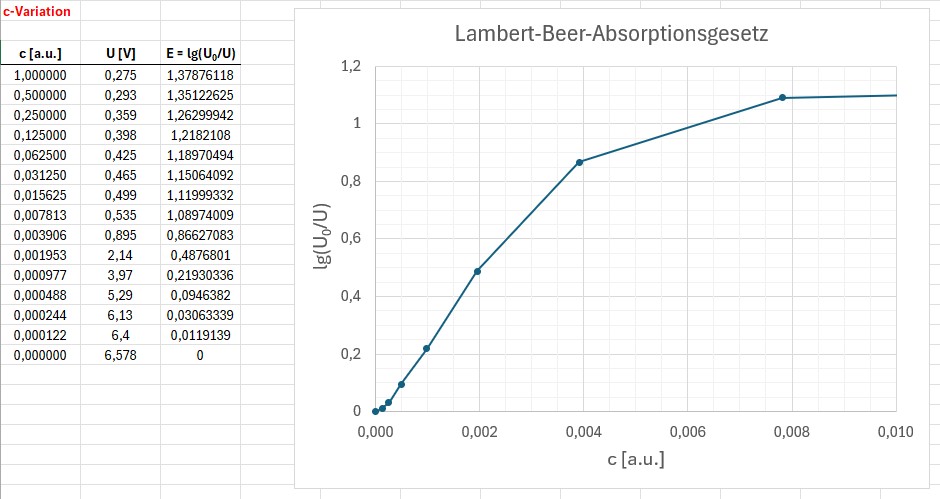
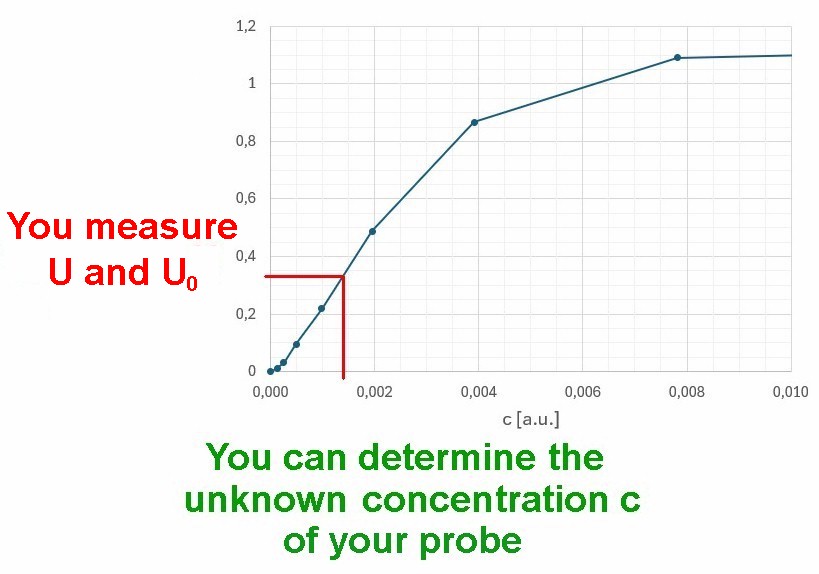
Zu Beginn verläuft der Graph (abgesehen von einem kleinen Bereich nahe dem Ursprung) wieder linear wie es nach dem Lambert-Beer-Gesetz der Fall sein sollte. Für größere Konzentrationen c flacht die Kurve allerdings wieder ab und das Gesetz gilt nicht mehr. Dies sieht man sehr deutlich in folgender Abbildung, wo noch höhere Konzentrationen vorkommen:

Kenne ich nun die konkrete lineare Beziehung zwischen E = lg(U0/U) und der Konzentration c, so kann ich bei einer unbekannten Probe durch Messung von U0 und U deren unbekannte Konzentration c ermitteln. Genau so wird es in Labors gemacht…
Das Youtube-Video reiche ich wie immer nach…

