Gyrocar
Unter einem Gyrocar versteht man ein Fahrzeug mit weniger Rädern als im Normalfall (zum Beispiel nur zwei oder wie bei meinem Gyrocar sogar nur eines), welches sich durch einen Kreisel stabilisiert.

Bildquelle: https://de.wikipedia.org/wiki/Einschienenbahn_am_Taunusrand#/media/Datei:Einschienerp.jpg, public domain
Wie stabilisiert nun ein Kreisel ein solches Gefährt? Nun betrachten wir folgenden Kreisel:
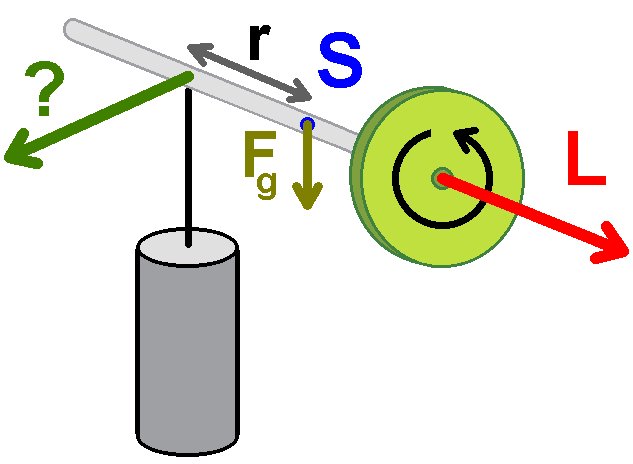
Durch die im Schwerpunkt S angreifende Kraft Fg und den Hebel r wirkt ein Drehmoment T, welches eigentlich den Kreisel nach unten kippen möchte:

Der rotierende Kreisel besitzt aber auch einen Drehimpuls L. Der Zusammenhang zwischen Drehmoment T und Drehimpuls L lautet: T = dL/dt. Das Drehmoment ist also proportional zur Änderung dL des Drehimpulses. Das bedeutet nun, dass sich die Drehimpulsachse des Kreisels verändert und zwar in horizontaler Richtung:

Diese zusätzlich zur Eigenrotation kommende Rotation nennt man Präzession. Deren Achse ist in diesem Fall die z-Achse. Der Kreisel beginnt durch das Drehmoment T sich also um die senkrechte Achse mit der Winkelgeschwindigkeit ωp zu drehen.
Jetzt kommt das sog. Kreiselmoment zum Tragen. Dreht sich ein Kreisel zusätzlich zur Eigenrotation um eine bestimmte Achse, so versucht das Kreiselmoment TKreiselmoment, die Kreiselachse parallel zu dieser Achse auszurichten. Konkret bedeutet dies also, dass das Kreiselmoment die Kreiselachse parallel zur z-Achse ausrichten möchte, ihn also aufrichten möchte.
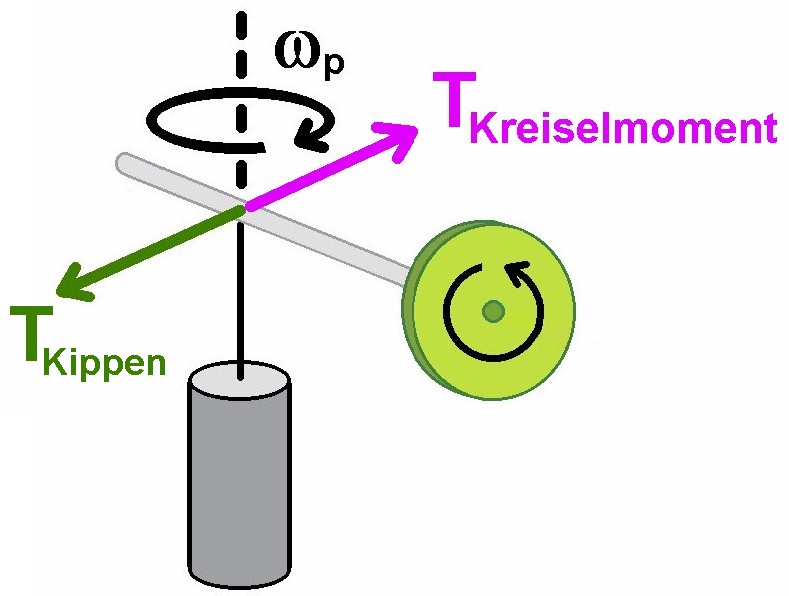
Genau dieses Kreiselmoment ist nun gleich groß wie das Kipp-Drehmoment TKippen. Demzufolge kippt der Kreisel nicht mehr und rotiert/präzessiert weiter in der horizontalen Ebene. Beim Gyrocar wirkt nun das Kreiselmoment gegen ein etwaig vorhandenes Kippen und stabilisiert so das Gyrocar.
Für den Bau eines Gyrocars benötigt man
- einen kleinen Metallkreisel (Amazon)
- eine Seilrolle (https://www.amazon.de/dp/B0BZPR4133)
- eine Plastikdose, zum Beispiel eine Fahrradtrinkflasche
- einen kleinen Elektromotor
- einen Batteriehalter







Die Motorhalterung habe ich mir 3D-drucken lassen:
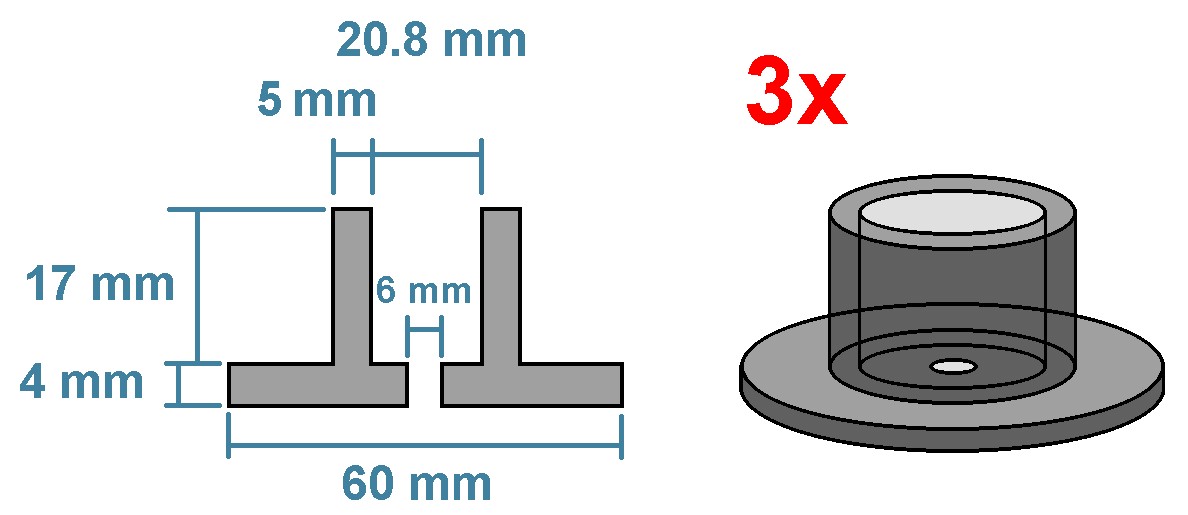
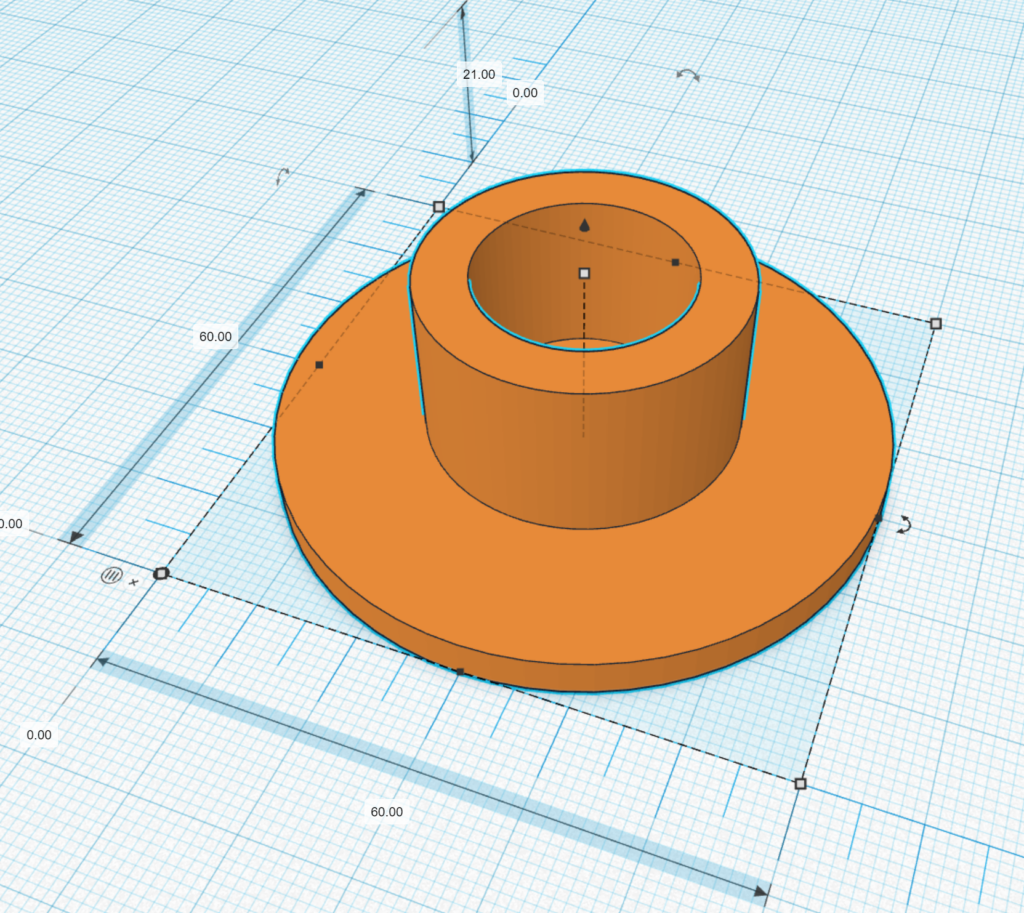


Die volle Achse des Gyroskops habe ich mit einem Hammer herausgeschlagen und nun durch zwei Messingrohre (6mm/4mm bzw. 4mm/2mm) ersetzt:



Das 4mm/2mm Messingrohr für die innere Achse:



Der Kreisel in seiner Halterung:





Die am Boden der Fahrradflasche montierte Seilrolle:


Als Teststrecke diente meine Siebschüssel:



Das Gyrocar war aber extrem instabil und kippte sofort um. Daher musste ich die Batteriebox vom Gyrocar trennen. Erst jetzt konnte ich einige Runden mit dem Gefährt drehen…
Da mich diese Situation aber nicht befriedigte, überlegte ich mir folgende Lösung: Die beiden Batterien kommen an die Unterseite des Gyrocars, um den Schwerpunkt näher an die Laufradachse zu bringen. Dies sollte eigentlich der Stabilität dienlich sein, mal schauen.
So, die Batteriebox ist auf die Unterseite gewandert aber das Ergebnis damit war mehr als ernüchternd. Das Gyrocar war in keinster Weise stabil und kippte nach kürzester Zeit um. Hätte ich so nicht erwartet…

Also schnell wieder abgebaut und es mit einer leichten Liion-Batterie auf der Oberseite probiert. Die liefert allerdings rund 4V und überlastet somit sowohl Motor als auch sich selbst. Aber unproblematisch für einen kurzen Lauf…


Damit balanciert das Gyrocar einigermaßen stabil auf der Schüssel, bleibt aber mangels Antrieb zumeist auf derselben Stelle stehen. Insgesamt bin ich mit den Ergebnissen meines Gyrocars nicht wirklich zufrieden. Ich hätte mir eine weitaus größere Stabilität erwartet, zumal sich der schwere Kreisel doch sehr schnell dreht. Eventuell eiert mein Kreisel aber zu sehr bzw. ist die Austarierung nicht hundertprozentig. Mal schauen, vielleicht baue ich es ja komplett neu auf…
Zauber-CD
Bei der Firma Winkler (https://www.winklerschulbedarf.com/) bin ich auf eine nette Spielerei zum Thema Kreisel gestoßen und zwar die sog. Antischwerkraftscheibe:
Für meinen Sohn und seine Arbeit habe ich dann auch gleich einige andere Dinge (Flugzeuge, Luftrakete usw.) mitbestellt….




Es mussten nur wenige Löcher gebohrt und die Kabel verlötet werden:



Die fertige Antischwerkraftscheibe:

Kollergang
Zum Thema Kreisel hätte ich noch einen schönen Versuch und zwar den sog. Kollergang. Dabei handelt es sich um eine Achse mit 2 Rädern, welche um eine zweite Achse senkrecht dazu gedreht wird:
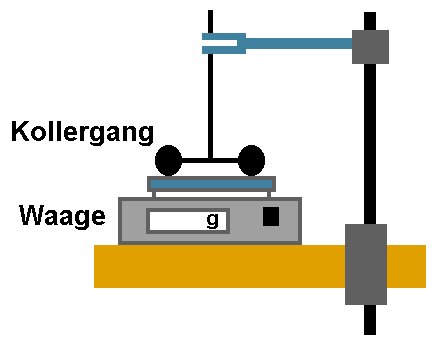
Das besondere hier ist der Umstand, dass durch die Rotation des „Kreisels“ dessen Kraft auf die Unterlage gesteigert werden kann. Schuld ist das sog. Kreiselmoment T = ωp × L (siehe auch weiter oben). Dieses möchte ja die Drehimpulsachse L parallel zur aufgezwungenen Drehachse ωp ausrichten. Im konkreten Fall also die beiden Achsen der zwei Räder nach unten kippen. Dadurch erhöht sich die Kraft der abrollenden Räder auf die Unterlage. Mit einer Waage lässt sich dann diese zusätzlich zum Gewicht wirkende Kraft in Abhängigkeit von der Winkelgeschwindigkeit ωp ermitteln.
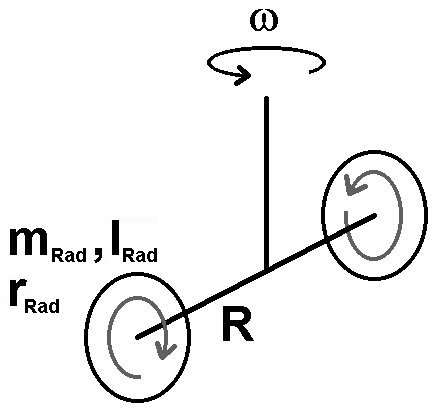
Drehen sich die beiden Räder mit der Winkelgeschwindigkeit ω um die vertikale Achse, so beträgt die Bahngeschwindigkeit am Ort der beiden Räder v = ω · R. Die Winkelgeschwindigkeit der Räder um ihre Achse beträgt dann ωRad = v / rRad = ω · R / rRad. Für den Drehimpuls eines Rades ergibt sich dann der Ausdruck LRad = I · ωRad = I · ω · R / rRad.
Das Drehmoment lautet somit: TRad = LRad · ω = I · ω² · R / rRad.
Mit diesem Ausdruck lässt sich dann auch die Kraft F eines Rades auf die Unterlage bestimmen und zwar gilt: TRad = FRad · R ⇒ FRad = TRad / R = I · ω² / rRad.
Die von der Waage angezeigte, zusätzliche Kraft lautet daher: FWaage = 2 · FRad = 2 · I · ω² / rRad und sollte daher eine ω²- bzw. f²-Abhängigkeit zeigen.

Den Kollergang werde ich aus LEGO-Teilen basteln. Durch meine vorherigen Versuche mit LEGO-Teilen habe ich noch ein kleines Sortiment übrig. Mal schauen, was alles zu finden ist bzw. was noch über http://www.willhaben.at bestellt werden muss.

Bestellt werden mussten nur die beiden Räder, den Rest hatte ich in meinem Fundus. So sieht das Gestell aus:



Die LEGO-Technikachse habe ich in einen Achsadapter (2 mm auf 4 mm) geklebt:

Hier der gesamte Aufbau mit Stativ, Waage und Arduino-Drehzahlmesser:







Die ermittelten Messwerte m = m(f):
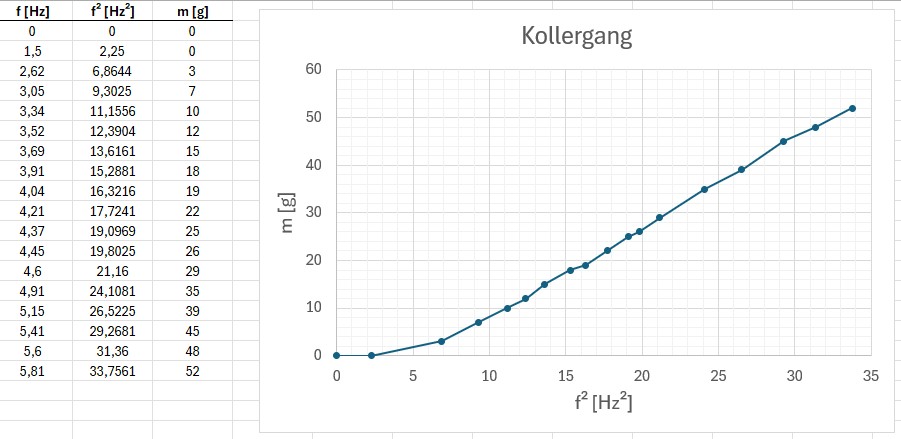
Wie zu erwarten war erhalte ich eine einigermaßen schöne f²-Abhängigkeit der mit der Waage angezeigten Masse/Kraft, Heureka 😉
Zum Abschluss wie gewohnt das Youtube-Video:
Zauberschachtel
Bewegt man einen Kreisel, so treten Kreiselmomente auf. Sie versuchen die Drehimpulsachse L parallel zur aufgezwungenen Drehachse ω auszurichten. Dadurch enstehen Kräfte, welche zum Beispiel Bewegungen stabilisieren, man denke nur ans Fahrradfahren. Verbaut man einen Kreisel in einer Schachtel, so vollführt diese „eigenartige“ Bewegungen. Zum Beispiel kippt sie nicht, sondern sie beginnt sich zu drehen. Genau um eine solche Zauberschachtel soll es bei diesem Experiment gehen.

Als Kreisel missbrauchen wir eine alte Computer-Festplatte. Diese erhält man für kleines Geld gebraucht zum Beispiel auf http://www.willhaben.at. Am besten hält man Ausschau nach einer alten IDE Festplatte mit mindestens 2 Speicherscheiben. Welches Modell über 2 oder mehr Speicherscheiben verfügt, kann man z.B. durch ChatGPT erfahren. Zunächst muss man die Festplatte öffnen und von unnötigen Balast befreien.


Hier erkennt man die beiden Speicherscheiben/Platter:

Der entfernte Arm mit den Leseköpfen:

So sieht es schon gleich besser aus:

Zwichen den beiden Platten befindet sich eine Distanzscheibe, welche entfernt werden muss:

Anstelle der Distanzscheibe werden nun Speicherscheiben anderer Festplatten montiert. Bei mir war Platz für insgesamt 4 Scheiben vorhanden. Dadurch erhöhen wir die drehende Masse unseres Kreisels und damit seinen Drehimpuls.

Für die Spannungsversorgung habe ich mir ein kleines 12V/5V-Netzteil gebastelt. Gespeist wird dieses von zwei 18650-Liion-Akkus. Für die 12V benötigt man einen Step up-Wandler (Boost Converter), für die 5V einen Step down-Wandler (Buck Converter). Am Ende wird dann ein Molex-Stecker angelötet mit Gelb = +12V, Rot = +5V, Schwarz = Ground/Minus:



Ein erster Test verlief allerdings ernüchternd. Der Festplattenmotor fährt zwar zu Beginn hoch, aber nach ca. 10 sek hört er wieder auf sich zu drehen und die Speicherscheiben kommen langsam wieder zum Stillstand. Scheinbar benötigt der Festplattencontroller irgendwelche Signale/Daten von den entfernten Leseköpfen. Ich habe 4 weitere alte Festplatten bestellt. Vielleicht gelingt es mir ja zumindest eine davon dauerhaft zum Rotieren zu bringen.
Falls dies scheitert, werde ich den Festplattenmotor über einen Brushless-ESC ansteuern. Dazu habe ich mir einen solchen auf Aliexpress samt Servotester zum Verstellen der Geschwindigkeit bestellt.
Der Festplattenmotor besitzt 4 pins, wobei für den Betrieb nur 3 benötigt werden. Um herauszufinden, welche dies sind, müssen die Widerstände zwischen zwei benachbarten Pins gemessen werden. In zwei Fällen sind die Werte gleich und höher, zwischen einem Paar misst man einen niedrigeren Widerstand. Hier gibt es ein gutes Anleitungsvideo: https://www.youtube.com/watch?v=mNtPa9mxG_g.

Die 4 weiteren HDD sind angekommen und ich konnte sie gleich testen. Bei 2en drehte sich der Motor überhaupt nicht, bei den anderen beiden jedoch ohne Probleme. Jetzt kam aber die Stunde der Wahrheit: Dreht er sich auch noch ohne Lesekopf? Und ja, beide drehten sich anstandslos und fuhren nicht etwa nach kurzer Zeit wieder runter. Im microcontroller.net Forum wurde mir ja prophezeit, dass keiner der Motoren sich drehen wird. Da ich mich aber von solchen Dingen nicht abhalten lasse, überprüfte ich es getreu dem Motto „Probieren ist besser als Studieren“ praktisch und hatte Erfolg. Wenn ich immer nach solchen Unkenrufen gegangen wäre, hätte ich wohl 50% meiner Physikprojekte nicht umgesetzt.

Die erste funktionierende Festplatte war die Seagate Barracuda ATA IV Modell ST380021A mit 80 GB:




Die zweite funktionierende Festplatte war die Western Digital WD Caviar 307AA mit 30.7 GB:



Der Abstand der beiden Speicherscheiben war hier sehr groß, sodass im Anschluss dann sehr viele weitere Scheiben eingesetzt werden konnten:




Hier 3 Standbilder aus einem Video:



So, mittlerweile habe ich den ganzen Aufbau in einen Schuhkarton verfrachtet:



Leider bin ich mit den Ergebnissen überhaupt nicht zufrieden. In einer bestimmten Schieflage verhält sich der Karton zwar „eigenartig“ wie erwünscht, kippe ich ihn aber um die Längsachse, passiert so gut wie gar nichts. Deshalb bastel ich mir gerade aus Pappelholz eine maßgeschneiderte Holzbox.




Um alles so kompakt wie möglich zu gestalten, ging ich von zwei seriellen 18650-Akkus auf einen einzelnen zurück in Kombination mit zwei kleineren step up Wandlern. Jetzt lief der Motor aber gar nicht mehr an. Also wieder zurück zu 2 Akkus und stärkeren Spannungswandlern. Bei 8 V Versorgungsspannung zieht der Aufbau zu Beginn beim Anfahren immerhin rund 3.5 A. Zur Fixierung der Festplatte habe ich mir noch längere 6-32 UNC Schrauben besorgt. Wenn diese angekommen sind, kann ich den Aufbau fertigstellen…
Ich war ein wenig ungeduldig und habe mir 4 zöllige Schrauben im nächsten Computerladen besorgt. Damit konnte ich dann die Festplatte festschrauben und die Box vollenden:




Aber auch mit dieser maßgeschneiderten Holzbox waren die Ergebnisse leider nicht berauschend. Wenn man die Box in der Hand hält und Bewegungen vollführt, merkt man die Kreiskräfte recht deutlich. Stellt man die Box allerdings leicht gekippt auf den Boden, so fällt sich nach wie vor relativ rasch auf den Boden. Ich hatte mir ja erhofft, dass sie schräg stehend eine Präzession vollführt und somit dem Kippen auf längere Zeit widersteht. Viel kleiner und leichter kann ich die Box aber nicht machen.
Nachtrag: Ich kann die Box doch noch um einiges abspecken und zwar indem ich auf das Metallgehäuse der Festplatte verzichte. Also schnell einmal die Platine ausgebaut und den Brushless-Motor mit seinen 4 pads über Kabel mit der Platine verlötet.







Spannung angeschlossen und der Motor startet nicht mehr, sondern ruckelt vor sich hin bzw. bleibt stehen. Also dachte ich mir zunächst, ich habe beim Löten eines der pads zerstört. Daher lötete ich nun die 4 Kabel direkt an die sehr dünnen Motordrähte an. Zuvor musste ich mit dem Lötkolben noch die Schutzschicht entfernen. Spannung wieder angeschlossen und der Motor spinnt nach wie vor. Vielleicht kann es an den nicht montierten Speicherscheiben liegen? Diese angeschraubt und siehe da, jetzt läuft der Motor wieder wie erwünscht an. Hatte schon befürchtet, alles in die Tonne werfen zu müssen.


Alles in die Holzbox verfrachtet und einen finalen Test unternommen. Die Box kippt nun eine Spur langsamer zu Boden. So richtig zufrieden bin ich mit dem Ergebnis aber bei weitem nicht. Ich bin mir aber dessen bewusst, dass ich für einen richtigen Kreiselkoffer sehr tief in die Geldtasche greifen müsste. Und dies habe ich aber nicht vor. Also muss ich mich mit dem bescheidenen Resultat begügnen. Wer mich kennt, weiß dass mir dies nicht leicht fällt 😉
Nachtrag:
Der Vollständigkeit halber füge ich dies hier noch an. Habe mir ja einen Brushless-Motortreiber auf aliexpress gekauft. Dieser hat bekanntlich 3 Ausgänge, der brushless-Festplattenmotor aber 4. Man misst mit einem Ohmmeter einfach die Widerstände zwischen jeweils zwei benachbarten Anschlüssen. Ergibt sich zwischen zweien ein niedrigerer Wert, so muss der linke/rechte davon nicht angeschlossen werden.





Der Motor dreht sich sehr schön und lässt sich über den Servotester in der Drehzahl regeln…


