Viele werden mit dem Begriff Interferenz zum Teil etwas anfangen können und schon einmal etwas von konstruktiver bzw. destruktiver Interferenz gehört haben. Bei der Interferenz handelt es sich um eine Überlagerung etwa von Lichtwellen. Trifft Wellenberg auf Wellenberg so verstärkt sich die Welle und man spricht von konstruktiver Interferenz.
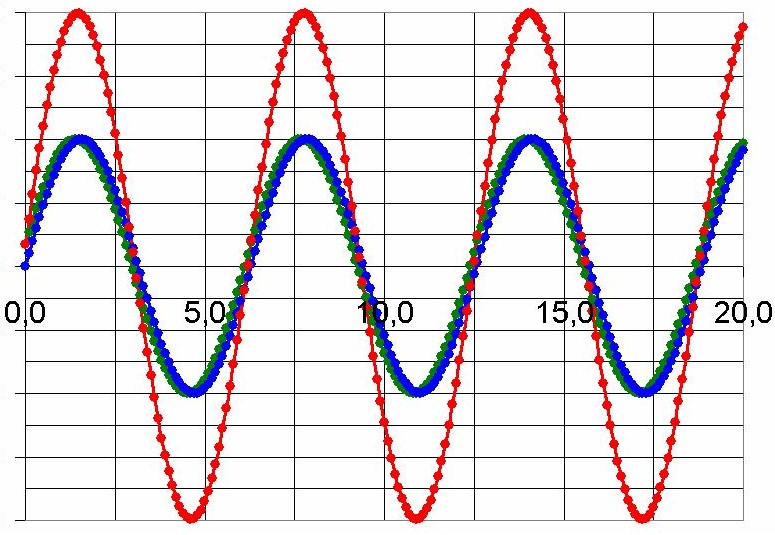
Kommen aber Wellenberg und Wellental zusammen, so löschen sich die Wellen aus und es ergibt sich eine destruktive Interferenz.
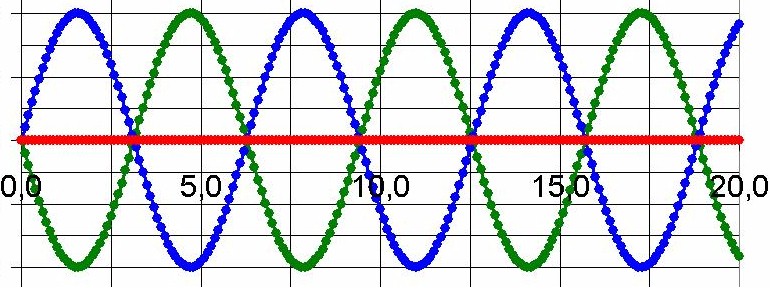Jeder hat wohl schon die Muster auf einer Seifenblase oder in einer Ölpfütze gesehen. Diese kommen genau aufgrund von Interferenz zustande und zwar beim Vorhandensein von sehr dünnen Schichten. Die Seifenblase ist sehr dünn und die Ölschicht im Wasser ebenso.
Bildquelle: https://www.experimente.physik.uni-freiburg.de/Optik/interferenzundbeugung/interferenz/interferenzankeilfoermigerseifenlamelle
Bei den sog. Newtonringen (https://stoppi-homemade-physics.de/newtonsche-ringe/) haben wir es auch mit Interferenz an dünnen Schichten zu tun. In diesem Fall ist es die dünne Luftschicht zwischen den beiden Gläsern, welche Interferenzerscheinungen erzeugt.
Betrachten wir eine zwischen zwei halbdurchlässigen Spiegeln eingeschlossene dünne Luftschicht:
Eine Lichtwelle durchdringt den Zwischenraum ohne Reflexion. Eine zweite Lichtwelle wird rechts an der Spiegelschicht reflektiert und links genauso. Sie hat also einen um 2·L längeren Weg als Welle 1 zurückzulegen. Immer wenn dieser Wegunterschied 2·L genau einem Vielfachen der Wellenlänge λ entspricht, treffen Wellenberg der Welle 1 auf Wellenberg der Welle 2 und es kommt zur konstruktiven Interferenz.
Diese Bedingung 2·L = n·λ wird bei konstantem L für verschiedene Wellenlängen λ erfüllt. Einmal gilt zum Beispiel 2·L = n·λ1 und dann 2·L = (n+1)·λ2. Beide Wellenlängen λ1 und λ2 werden konstruktiv verstärkt und die Transmission ist bei diesen Wellenlängen also hoch.
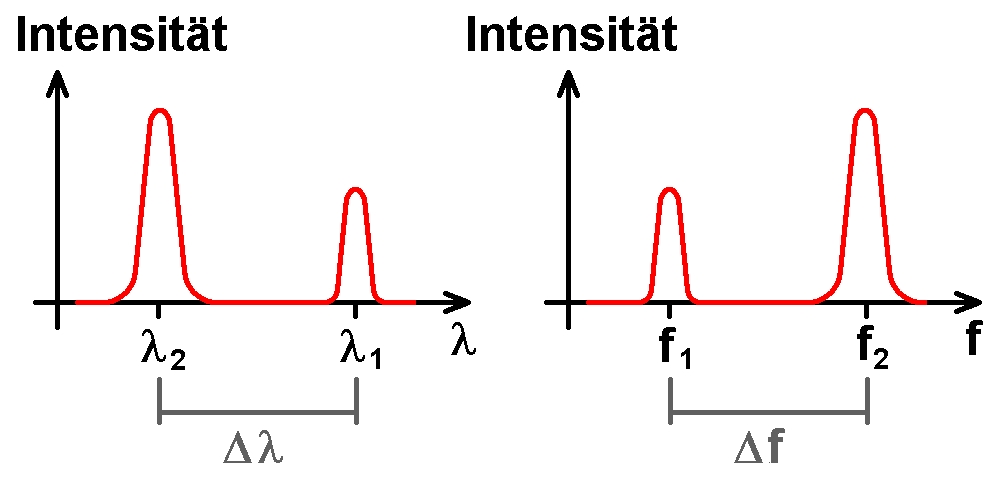
Es können also immer nur ganz bestimmte Wellenlängen das aus den beiden halbdurchlässigen Spiegeln gebildete Interferometer durchdringen. Genau dies gilt es experimentell zu erfassen. Als halbdurchlässigen Spiegel verwende ich immer jene von PGI bzw. Astromedia:
Diesen habe ich mit einem Glasschneider halbiert. Beleuchtet wird das Interferometer mit einer Glühbirne. Wir benötigen ja für diesen Versuch ein möglichst kontinuierliches Spektrum und eine Glühlampe erfüllt diese Bedingung ausgezeichnet.
Das das Interferometer durchdringende Lichtspektrum nehme ich mit meinem Lichtleiter-Webcam-Spektrometer auf. Den Eintritt des Lichtleiters postiere ich gleich hinter dem Interferometer.
Hier mein selbstgebautes Spektometer mit dem Lichtleiter:
Betrachtet man das Interferometer genauer, so kann man Interferenzmuster mit freiem Auge erkennen. Diese sind aber konkret nur sehr schwach ausgeprägt und lassen sich daher äußert schwer fotografisch erfassen:
Das aufgenommene Spektrum:
Man erkennt anhand der Intensitätspeaks deutlich, dass wie zu erwarten war nur bestimmte Wellenlängen das Interferometer durchdringen können.
Kann man nun diese Maxima auch theoretisch herleiten? Wir kennen ja die Interferenzbedingung 2·L = n·λ. Darauf aufbauend gilt:
Es gibt auch einen Online-Rechner zur Berechnung der Transmissions-Wellenlängen: https://www.filmetrics.com/reflectance-calculator?wmin=400&wmax=700&wstep=1&angle=0&pol=s&units=nm&mat[]=SiO2&d[]=0&mat[]=Al&d[]=15&mat[]=Air&d[]=1600&mat[]=Al&d[]=15&mat[]=SiO2&d[]=0&sptype=t
Trägt man dort etwa für den Luftspalt eine Dicke L = 7590 nm ein, so stimmen die theoretisch ermittelten Peaks recht gut mit meinem experimentellen Ergebnis überein:
Zum Abschluss der Vergleich Theorie-Experiment:
Gestoßen bin ich auf dieses schöne Projekt übrigens hier: https://www.instructables.com/Optically-Measure-Nanometer-Distances-on-the-Dinne/
Zum Schluss noch mein dazugehöriges Youtube-Video:
