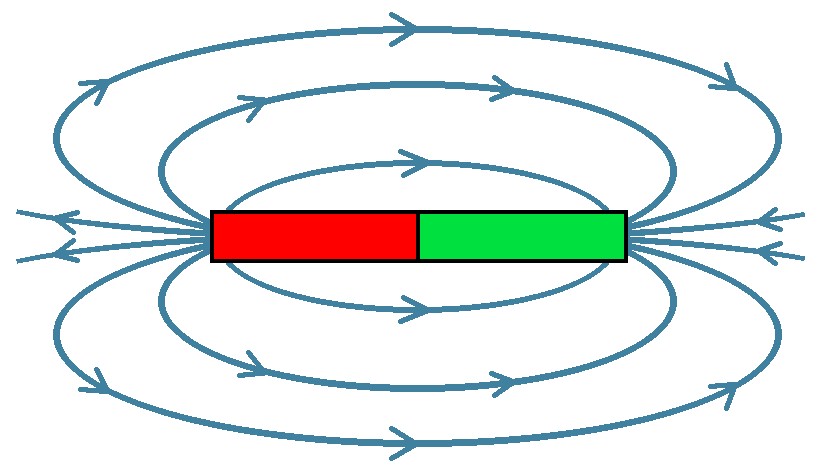
Elektrische und magnetische Felder

Fast jeder hat schon einmal den Verlauf der magnetischen Feldlinien zum Beispiel eines Stabmagneten gesehen. Die Feldlinien zeigen sowohl die lokale Richtung des Felds, als auch dessen Stärke mittels der Feldliniendichte an. Eng beieinander liegende Feldlinien symbolisieren ein starkes Feld und vice versa. Die elektrische Feldstärke E ist die Kraft F auf die Einheitsladung Q = +1 As. Daher ergibt sich für die Kraft auf die allgemeine Ladung Q der Ausdruck F = E · Q.

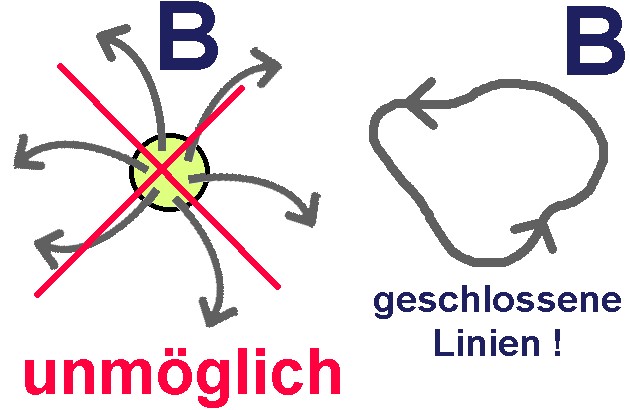
Elektrische Felder weisen von einer positiven Ladung weg bzw. hin zu einer negativen Ladung. Das elektrische Feld besitzt also meistens (Anm.: Es gibt auch elektrische Wirbelfelder) Quellen.´, von denen es ausgeht bzw. in die es mündet. Magnetfelder besitzen dagegen keine Quellen, aus denen sie hervortreten. Magnetische Felder sind Wirbelfelder und immer in sich geschlossen. Daher stimmt die obige Abbildung nur bedingt. Eigentlich hätte ich noch Feldlinien innerhalb des Stabmagneten zeichnen müssen und zwar vom grünen Südpol hin zum roten Nordpol. Es gibt also keine magnetischen Monopole wie etwa beim elektrischen Feld, aus denen die Magnetfeldlinien nur heraustreten wie unten links dargestellt. Diese Quellenfreiheit des magnetischen Feldes zeigt sich auch in dem Ausdruck div B = 0 (Anm.: div = Divergenz) der Maxwellgleichungen.

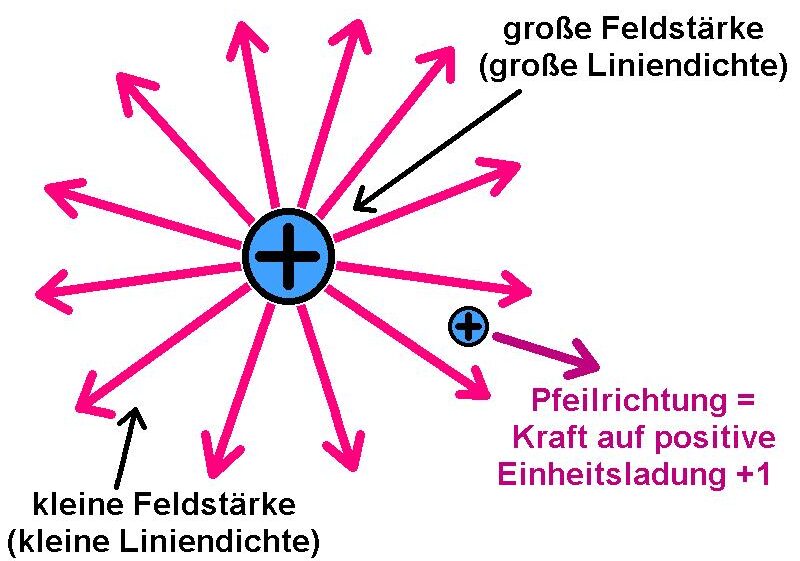
Der Feldverlauf einer einzelnen Punktladung sieht zum Beispiel wiefolgt aus:

In diesem Beitrag soll es um die Sichtbarmachung elektrischer und magnetischer Felder gehen.

Elektrische Felder

Für die Darstellung elektrischer Felder benötigt man ein Hochspannungsnetzteil, Elektroden, eine flache Glasschale, Öl und Grieß. Als HV-Netzteil verwende ich meines auf Basis eines CCFL-Inverters mit nachgeschalteter Kaskade. Dieses liefert eine Gleichspannung bis zu 15 kV.

Für die unterschiedlichen elektrischen Felder habe ich einige Elektroden aus starrem Kupferdraht geformt.

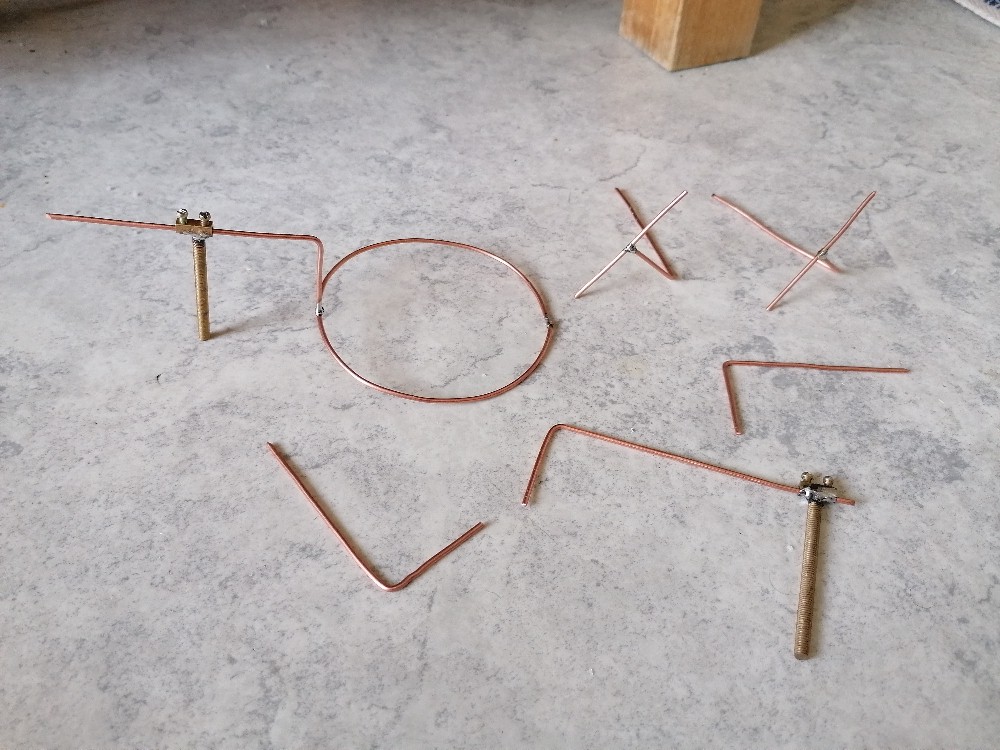
Damit ich diese bequem wechseln und ausrichten kann, lötete ich eine Lüsterklemme auf eine Messinggewindestange:

Als Öl kommt Silikonöl mit einer Viskosität von 300 cSt zum Einsatz. In der Literatur wird eigentlich Rizinusöl empfohlen, das wollte ich dann aber nicht extra für dieses Experiment besorgen.

Der gesamte Aufbau auf dem Küchenboden:

Noch ohne Spannung:

Mit angelegter Spannung (ca. 15 kV):

Die äußere Elektrode erwies sich als zu groß vom Durchmesser her. Deshalb lötete ich einen kleineren Kreis:

Die radial verlaufenden Feldlinien decken sich gut mit der Theorie:

Simulation eines Plattenkondensators:

Im Inneren herrscht ein einigermaßen homogenes elektrisches Feld, also mit konstanter Feldstärke (konkret E = U/d).

Zum Schluss untersuchte ich die Feldlinien zweier Punktladungen/punktförmiger Elektroden:

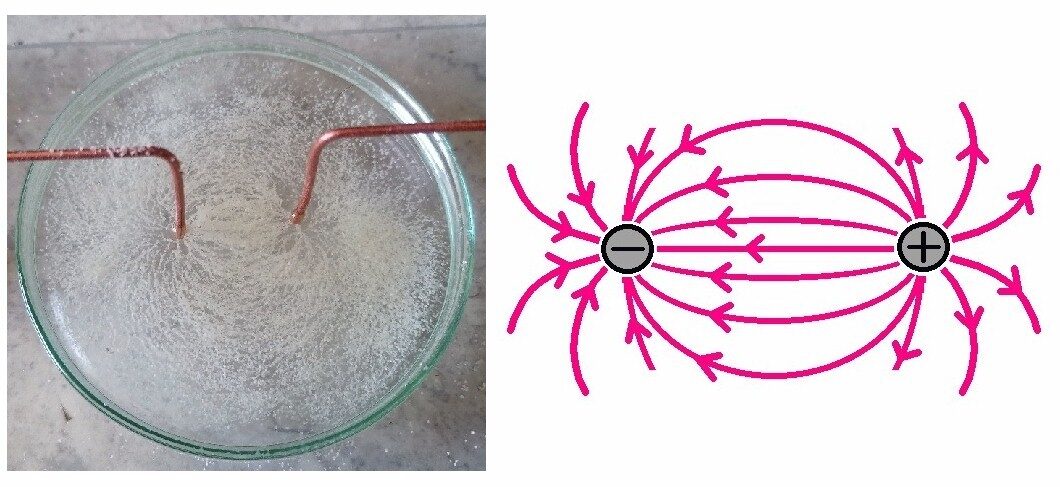
Magnetische Felder

Für die Darstellung magnetischer Felder benötigt man 2 mm starke Plexiglasplatten, Bohrer bzw. einen kegelförmigen Dremel-Schleifstein, Nadellager und einen Plexiglaskleber. Die Teile habe ich von aliexpress bzw. Amazon:

Ich habe mich für die 6 x 1 mm messenden Nadellager entschieden und 300 Stück davon bestellt:

Für die Löcher in der Plexiglasplatte verwendet man zum Vorbohren einen gewöhnlichen Bohrer. Für die endgültige Größe (in meinem Fall 7 mm) greift man dann aber besser zu einem kegelförmigen Schleifstein, denn mit einem Bohrer würde das Plexiglas reißen.

Meine Küche habe ich zwischenzeitlich wieder in eine Werkstatt umfunktioniert:

Für die fertige Lochplatte benötigte ich ca. 2 h und meine Finger hatten danach Blasen, denn den 6.8 mm Bohrer drehte ich zum Schluss per Hand vorsichtig in sämtliche Löcher.

Der leider ziemlich dünnflüssige Plexiglaskleber, wodurch am Ende ungewollt ca. 3 Löcher teileweise mit Kleber gefüllt waren und sich darin die Nadellager nicht mehr schön ausrichten können.