Die Ramanspektroskopie spielt heute bei der Analyse von Materialien eine wichtige Rolle. Benannt ist die sog. Raman-Streuung nach dem indischen Physiker und Nobelpreisträger Chandrasekhara Venkata Raman (1888 – 1970) benannt.

Bildquelle: Von Nobel Foundation – From Nobel Lectures, Physics 1922-1941, Elsevier Publishing Company, Amsterdam, 1965, Gemeinfrei, https://commons.wikimedia.org/w/index.php?curid=4213636
Sein Neffe war übrigens Subrahmanyan Chandrasekhar (1910 – 1995), welcher ebenfalls den Nobelpreis für Physik erhielt und zwar für seine theoretischen Studien der physikalischen Prozesse, die für die Struktur und Entwicklung der Sterne von Bedeutung sind. Nach ihm ist die sog. Chandrasekhargrenze für weiße Zwerge benannt, welche die Massenobergrenze für weiße Zwerge darstellt. Sie liegt bei rund 1.45 Sonnenmassen. Bei einer Supernova Typ 1a saugt ein weißer Zwerg in einem Doppelsternsystem Material von seinem Begleiter ab und wächst eben bis zu dieser Chandrasekhargrenze. Hat er diese erreicht, explodiert er und bildet eine Supernova Typ 1a. Da dies immer bei der gleichen Massengrenze erfolgt, sind Supernovae vom Typ 1a auch immer gleich hell und dienen deshalb als sog. Standardkerzen zur Bestimmung der Entfernung astronomischer Objekte.
Bei einer Streuung wird Licht von einem Körper/Partikel/Atom kurzfristig aufgenommen/absorbiert um dann gleich wieder emittiert zu werden. Dabei erfolgt bei dieser Absorption kein Sprung in ein reales, höheres Energieniveau, sondern in ein virtuelles Niveau (siehe Abbildung unten).

Überstreichen die beiden „Sprünge“ nach oben und unten diesselbe Energie, so spricht man von der sog. Rayleighstreuung. Das absorbierte Photon besitzt dann dieselbe Wellenlänge wie das emittierte. Bei der Ramanstreuung unterscheiden sich aber genau diese beiden Sprünge. Ist die bei der Emission freigewordene Energie geringer als die absorbierte, so spricht man von der Stokes Ramanstreuung. Die Wellenlänge des emittierten Photons ist somit größer/rotverschoben. Bei der Antistokes Ramanstreuung ist hingegen die Energie des emittierten Photons größer als jene des absorbierten Photons und damit die Wellenlänge in Richtung Blau verschoben.
Im Gegensatz zur Rayleigh-Streuung ist die Raman-Streuung viel intensitätsschwächer. Beim experimentellen Nachweis der Ramanstreuung überstrahlt also das „einfallende“ Licht zusammen mit der Rayleighstreuung die schwachen Raman-Linien. Man muss daher die beiden erstgenannten Lichtquellen mittels Filter nahezu komplett ausblenden.



Da ich experimentell einen 450 nm Laser verwende, benötige ich also einen Filter, welcher alle Wellenlängen knapp oberhalb von 450 nm oder knapp unterhalb von 450 nm absorbiert. Bei meiner Suche im Internet bin ich auf den Filter der Firma Schott mit der Bezeichnung GG475 gestoßen. Dieser scheint meine Wünsche zu erfüllen. Deshalb habe ich mir das chinesische Pendant mit der Bezeichnung JB470 um rund 20 Euro gekauft. Ramanfilter sind in der Regel sehr teuer und kosten mehr als 200 Euro. Daher bin ich schon neugierig, ob ich mit diesem günstigen Filter auch brauchbare Ergebnisse erzielen kann.
Normalerweise sieht man Raman-Spektroskope sehr oft mit einem grünen DPSS-Laser mit λ = 532 nm betrieben. Normalerweise müsste es aber auch mit meinem 450nm-Laser funktionieren. Wie man oben anhand des Termschemas sieht, liegen dann die Stokes- bzw. Antistokes-Linien ebenfalls bei geringerer Wellenlänge, denn der Anregungslaser zieht quasi die Ramanlinien mit seiner Wellenlänge mit. Zur Veranschaulichung dient das weiter unten abgebildete Termschema.

Quelle: SCHOTT

Da wie eben gesagt die im Spektrum auftauchenden Raman-Linien (Stokes und Antistokes) symmetrisch um die Anregungswellenlänge liegen und diese logischerweise variieren kann, macht es wenig Sinn die Wellenlänge der Stokes- bzw. Antistokes-Linien anzugeben. Stattdessen trägt man anstelle der Wellenlänge λ die sog. Raman-Verschiebung auf der Abszisse auf:
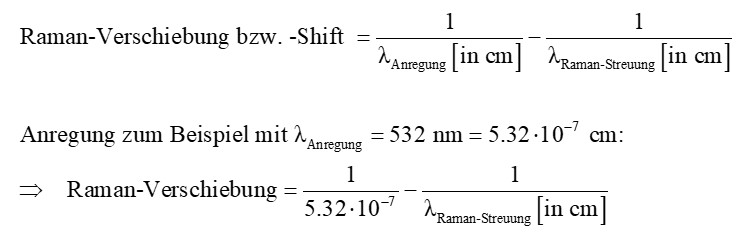

Diese Raman-Verschiebung ist proportional zur Energiedifferenz ΔE der beiden Sprünge und genau diese Energiedifferenz ist UNABHÄNGIG von der Wellenlänge der einfallenden Photonen! Stattdessen hängt sie nur von den streuenden Atomen ab. Dadurch kann die Raman-Streuung zur Spektroskopie verwendet werden.


Die Raman-Verschiebung entspricht also bis auf den konstanten Vorfaktor 1 / (h · c) genau der Energiedifferenz ΔE und diese Energiedifferenz entspricht genau dem Abstand der realen „unteren“ Energieniveaus. Würde man direkte Übergänge zwischen diesen unteren Energieniveaus beobachten wollen, so müsste das Spektroskop im Infrarotbereich sensibel sein. Denn diese geringen Energiedifferenzen bedingen durch E = h · f = h · c / λ eine geringe Frequenz f bzw. große Wellenlänge λ. Durch die Ramanstreuung werden diese im Infrarot liegenden direkten Übergänge in den sichtbaren Wellenlängenbereich quasi verschoben.

Der gesamte experimentelle Aufbau sieht wiefolgt aus:

Mit dem Beugungsgitter erfolgt die spektrale Zerlegung und Untersuchung des Lichts der Ramanstreuung. Hier noch eine Tabelle mit den zu erwartenden Raman-Shifts in Abhängigkeit von der funktionalen Gruppe:

Quelle: https://physicsopenlab.org/2021/12/31/17034/
Hier das mit Isopropanol zu erwartende Raman-Spektrum. Den höchsten Peak bei 819 cm-1 sollte ich ja hoffentlich detektieren können 😉
 Quelle: https://www.researchgate.net/publication/322449129_All-fiber_Raman_Biosensor_by_Combining_Reflection_and_Transmission_Mode/figures
Quelle: https://www.researchgate.net/publication/322449129_All-fiber_Raman_Biosensor_by_Combining_Reflection_and_Transmission_Mode/figures
Die Wellenlänge des blauen Lasers habe ich nun auch mit meinem Webcam-Spektroskop zu λ = 450–451 nm bestimmt. Die Transmission des bestellten Filters beginnt genau bei 451 nm zu steigen. Von daher könnte es mit dieser Kombination Laser-Filter funktionieren…



Für das Experiment benötigte ich Küvetten mit 4 optischen Fenstern. Dankenswerterweise hat mich hierbei die Firma Brand (https://shop.brand.de/de/) aus Wertheim/Deutschland gesponsert, vielen vielen Dank dafür 🙂



Auch der Filter ist heute noch eingetroffen. Er blockiert recht gut das 450 nm-Laserlicht. Blickt man aber durch den Filter direkt auf den Laser, so erkennt man schon noch eine nicht unerhebliche Strahlung. Ob diese dann die Ramanstrahlung im Spektrum überstrahlt, wird sich noch zeigen…




Das Ramanspektrum nehme ich ja mit meinem Smartphone auf. Dieses erlaubt mir Belichtungszeiten bis zu 30 sek, was für die schwachen Ramanlinien ausreichen wird. Vorher musste ich aber das Smartphone-Spektroskop mit Lichtquellen bekannter Wellenlänge kalibrieren. Hierfür verwendete ich drei Laserpointer mit λ = 650 nm, 532 nm und 405 nm. Ich bestimmte für alle drei Laser den Pixelabstand zwischen Maximum 0-ter und 1-ter Ordnung. Zum Einsatz kam ein Gitter mit 1000 Linien/mm.

Die Positionen der Maxima ermittelte ich mit der Freeware ImageJ:

Hier die Tabelle der für die drei unterschiedlichen Laser ermittelten Pixelpositionen:

Im Mittel entspricht also 1 Pixel einer Wellenlänge von 0.3122 nm. Zur Auswertung des Ramanspektrums brauche ich jetzt im Foto nur noch die Pixelabstände x0 – x1 bestimmen. Daraus kann ich dann die jeweiligen Wellenlängen im aufgenommenen Spektrum ermitteln. Zum Beispiel würde ein Pixelabstand der beiden Maxima von 1700 Pixel einer Wellenlänge λ = 1700 · 0.3122 = 530.7 nm entsprechen. Und kenne ich die Wellenlängen λ im Spektrum, kenne ich auch deren Ramanverschiebungen 1/(450 nm · 10–7) – 1/(λ · 10–7). Soweit der Plan…
Heute konnte ich das Experiment erstmals durchführen. Als Substanz kam 2-Propanol (C3H8O) zum Einsatz. Damit ich das sehr schwache Raman-Streulicht gut fotografieren konnte, bastelte ich mir aus Moosgummi eine Abdeckung mit Sichtfenster für die Küvette. Das Beugungsgitter mit 1000 Linien/mm befestigte ich mit Klebeband vor der Kamera des Smartphones. Damit der Laserstrahl dünner und damit das Spektrum schärfer wird, habe ich den Laser mit Alufolie umwickelt und mit einer Nadel ein dünnes Loch in die Folie gestoßen.





Ohne Filter konnte man nur das intensive blaue Laserlicht bzw. die Rayleigh-Streuung sehen:


Erst mit Filter und langer Belichtungszeit trat die Ramanstreuung in Erscheinung:


Hier muss man sehr aufpassen, nicht anstelle des sehr schwachen Ramanstreulichts das intensivere Fluoreszenzlicht der Plastikküvette aufzunehmen. Dies geschieht dann, wenn der Laserstrahl durch das vordere oder hintere Küvettenfenster strahlt und nicht mittig nur durch die zu untersuchende Flüssigkeit. Hier sieht man mein anfängliches Missgeschick:

Das Fluoreszenzlicht des Plastiks besitzt nämlich im Gegensatz zu Propanol ein kontinuierliches Spektrum, wie man hier erkennen kann:

Hier nun das richtige aber deutlich schwächere Linienspektrum der Ramanstreustrahlung von Propanol. Die Belichtungszeit mit meinem Smartphone betrug zwischen 20 und 30 Sekunden!


Hier eine kurze Anleitung, wie man mit der Software ImageJ den Intensitätsverlauf erhält und dann in EXCEL hochlädt:
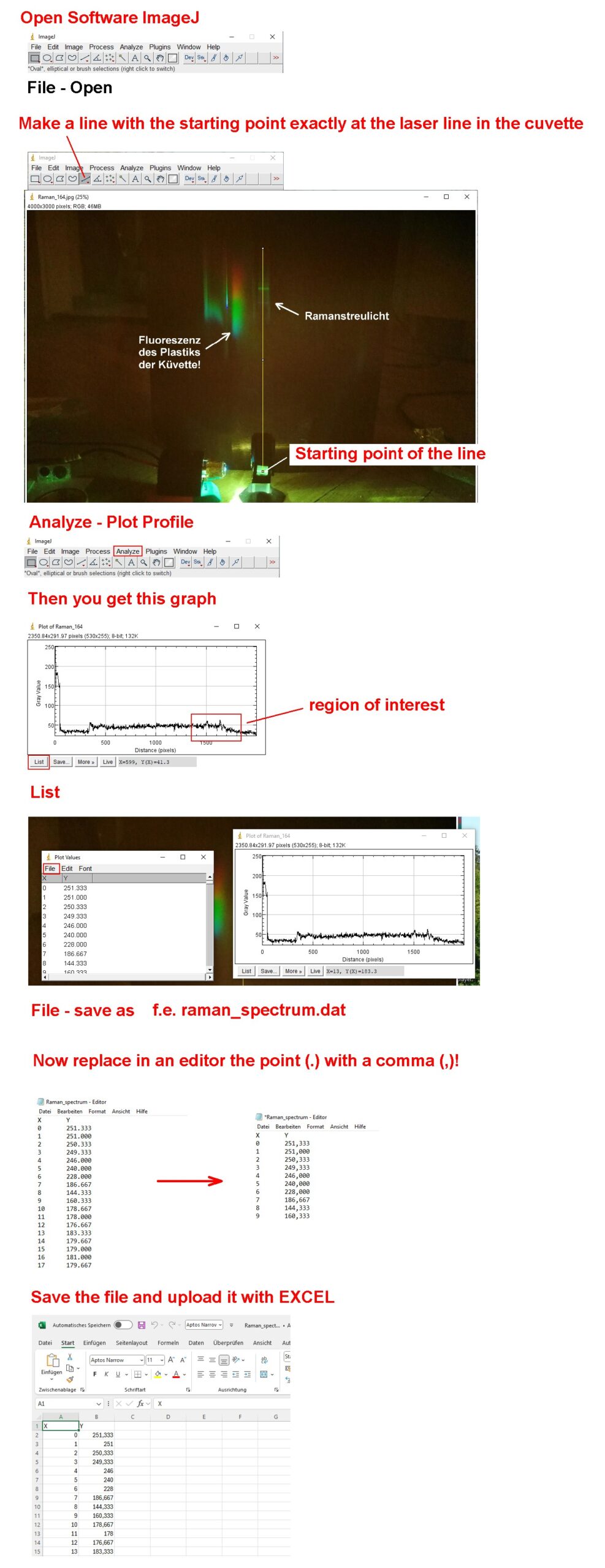
Wir haben ja zuvor bereits unser Spektrum mittels mehrerer Laserpointer kalibriert. Konkret erhielt ich zum Beispiel folgende Umrechnung: 0.3122 nm/Pixel. Mit diesem Faktor kann ich dann die Pixel-Nummer in der EXCEL-Tabelle in die Wellenlänge in Nanometer konvertieren. So besitzt etwa das Pixel 1457 die Wellenlänge 1457 · 0.3122 = 454.8754 nm. Kenne ich nun die Wellenlänge λ und die Laserwellenlänge λ0 (z.B. 450 nm = 450 · 10^ –7 cm), so kann ich in EXCEL eine weitere Spalte mit der Raman-Verschiebung (Raman-shift) = 1/λ0 [in cm] – 1/λ [in cm] einfügen.
Ich erhalte dann in EXCEL folgende Spalten und folgenden Graph, wobei mich nur jener Bereich des Spektrums mit einem Raman-shift > 0 interessiert:
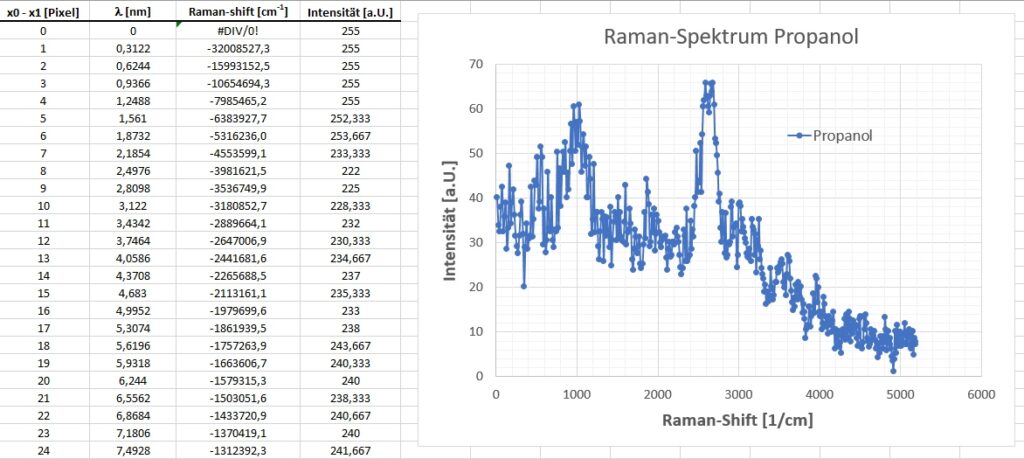

In meinem Ramanspektrum erkennt man 2 peaks etwa bei 950 cm–1 und bei 2700 cm–1. Dankenswerterweise hat mir Lodovico von PhysicsOpenLab (https://physicsopenlab.org/) sein Ramanspektrum von Propanal geschickt. Obwohl seines natürlich ungleich detailreicher und professioneller ist, erkenne ich in meinem doch einige Parallelen.

Bildquelle: https://physicsopenlab.org/2021/12/31/17034/ bzw. https://physicsopenlab.org/2022/01/20/raman-spectra-of-alcoholic-molecules/
Zum Abschluss noch das Youtube-Video:

