
Quelle: Wikipedia
Das nach den beiden Physikern Gustav Heinrich Wiedemann (1826 – 1899) und Rudolph Franz (1826 – 1902) benannte Gesetz verknüpft die thermische Leitfähigkeit λ mit der elektrischen Leitfähigkeit σ eines Stoffs und zwar in der Form

Bei einer bestimmten Temperatur T ist also der Quotient aus λ und σ für alle Metalle gleich. Ein besserer thermischer Leiter (größeres λ) leitet auch den elektrischen Strom besser (größeres σ = 1/ρ mit dem spezifischen Widerstand ρ) und vice versa. Daraus ist ersichtlich, dass die Wärmeleitfähigkeit eng mit der Bewegung der Elektronen zusammenhängen muss.
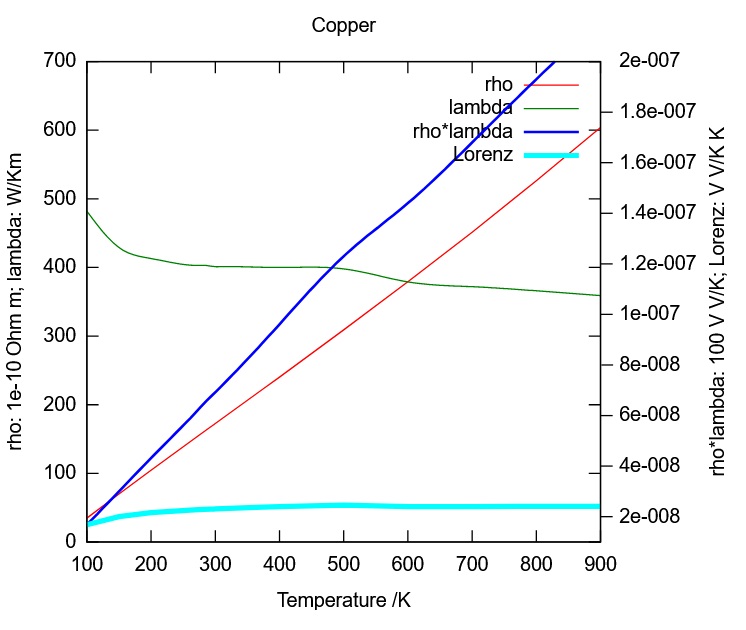
Quelle: Wikipedia
Die annähernd lineare Temperaturabhängigkeit des Quotienten λ/σ kommt nahezu ausschließlich von der Temperaturabhängigkeit von σ (bzw. ρ) und zwar sinkt σ mit steigender Temperatur. Metalle sind ja PTC-Leiter, d.h. ihr Widerstand nimmt mit zunehmender Temperatur zu.
Im Experiment zum Wiedemann-Franz-Gesetz wird es also darum gehen, die Wärmeleitfähigkeit λ und die elektrische Leitfähigkeit σ eines Metalls (konkret von Aluminium) zu bestimmen und die Lorenzzahl L zu berechnen. Wie gehe ich hierzu vor?
Die elektrische Leitfähigkeit ermittle ich über den elektrischen Widerstand R. Da dieser für ein Stück Aluminium sehr niedrig ist, kann ich dieses nicht einfach an ein gewöhnliches Multimeter anschließen. Ich benötige einen konstanten Strom von z.B. I = 1 A und messe den Spannungsabfall über dem Metall. In diesem Fall ist dann nach dem Ohmschen Gesetz U = I · R der Spannungsabfall U gleich dem ohmschen Widerstand R. Auf diese Weise können ohne Probleme Widerstände im mΩ-Bereich gemessen werden.
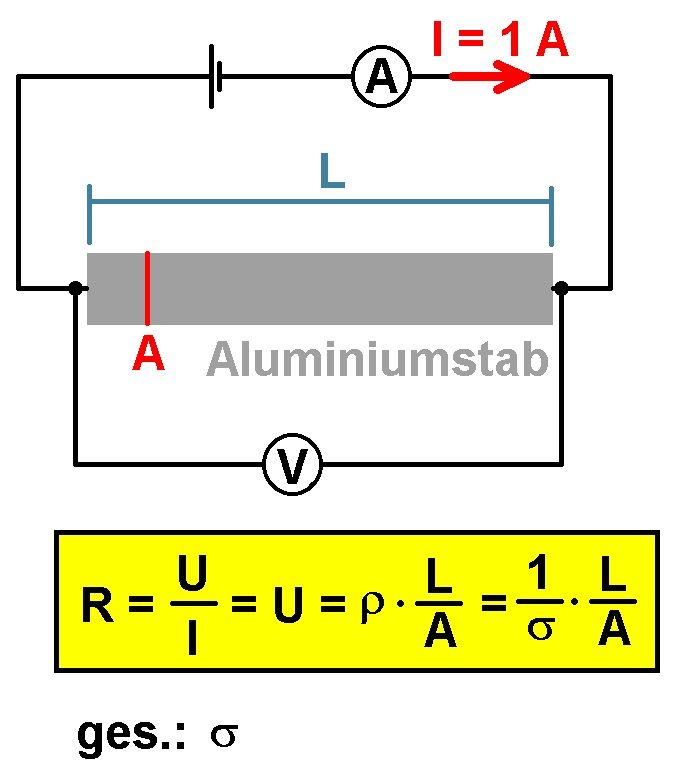
Kenne ich die Länge L (Achtung: hier nicht zu verwechseln mit der Lorenzzahl L!) und den Querschnitt A des Metalls, kann ich den spezifischen Widerstand ρ bzw. die elektrische Leitfähigkeit σ leicht bestimmen.
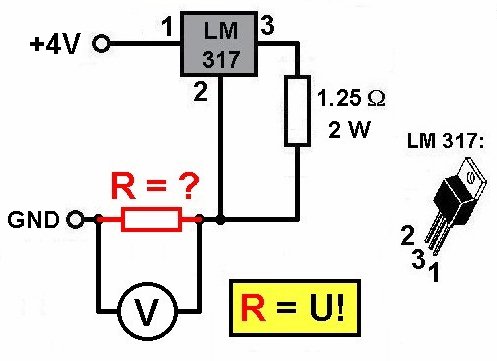


Für die Konstantstromquelle verwende ich den Spannungsregler LM317. Befindet sich zwischen Pin 2 und 3 ein Widerstand von genau 1.25 Ohm, so regelt der LM317 schön auf eine Stromstärke von I = 1 A nach.
Die Messungen zur elektrischen Leitfähigkeit konnte ich heute durchführen. Verwendet habe ich dazu einen eloxierten Aluminiumstab mit der Länge L = 0.4 m und dem Durchmesser d = 4 mm.




Bei einer Stromstärke von 1 A konnte ich einen Spannungsabfall von 1.0 mV messen. Der Widerstand betrug also 1.0 mΩ.



Mit diesen Werten ergab sich daher folgende elektrische Leitfähigkeit:

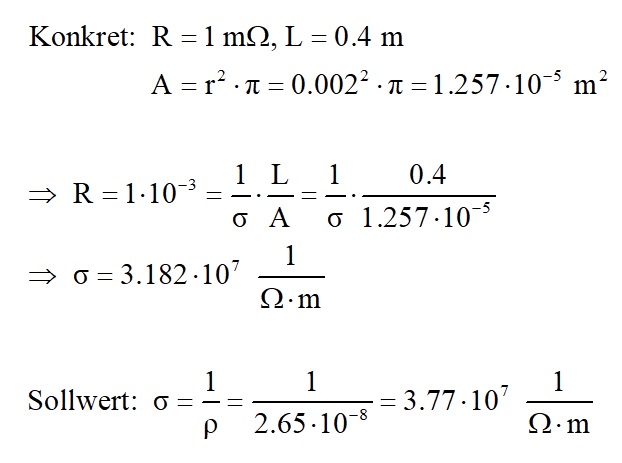
Wie bereits erwähnt, handelt es sich um einen eloxierten Aluminiumstab. Berücksichtigt man dies und nimmt eine Dicke der isolierenden Eloxalschicht von 15 µm an, so ergibt sich ein Radius von nur noch 1.97 mm und eine elektrische Leitfähigkeit σ = 3.28 · 10 ^ 7 1/Ω·m, also schon etwas näher am Sollwert. Zudem muss bemerkt werden, dass die Spannung mit dem Multimeter nur mit einer 0.1 mV-Auflösung gemessen wurde. Von daher ergibt sich eine recht große Unsicherheit für mein ermitteltes σ!
Da mir das Ergebnis doch zu sehr vom Sollwert abwich, habe ich das Experiment wiederholt und nun die Spannung mit meinem µV-Meter (Verstärkung = 1000) gemessen:



Ich komme nun auf eine Spannung von 0.858 mV. Dies eingesetzt in die Formel für den Drahtwiderstand liefert eine elektrische Leitfähigkeit von 3.71 · 10 ^ 7 1/Ω·m, was nun deutlich näher am Sollwert für Aluminium liegt. 😉
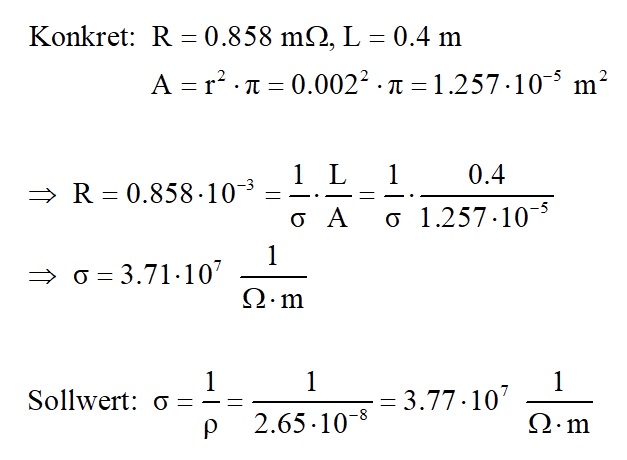
Wie ermittle ich aber nun experimentell die Wärmeleitfähigkeit? Hier benutze ich die Definitionsformel für λ:
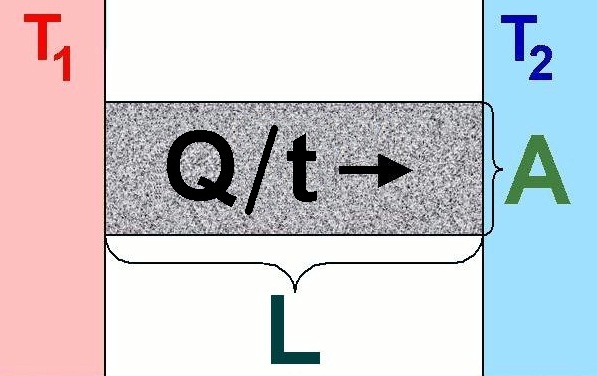

Auch hier darf die Länge L nicht mit der Lorenzzahl L im Wiedemann-Franz-Gesetz verwechselt werden! Experimentell gehe ich folgendermaßen vor:
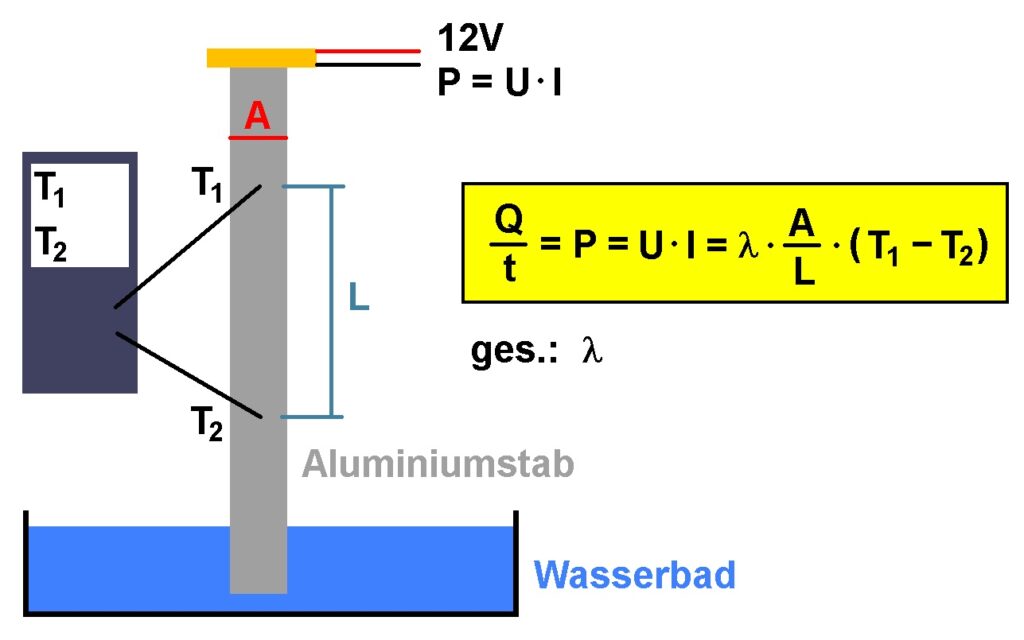
Ich stelle einen Aluminiumstab mit der Querschnittsfläche A in ein Wasserbad. Am oberen Stabende befindet sich eine mit Wärmeleitkleber aufgebrachte Heizplatte. Deren zugeführte elektrische Leistung P = U · I entspricht weitestgehend dem Wärmestrom Q/t. Im Abstand L messe ich mit meinen Thermometer die Temperaturen T1 und T2. Daraus lässt sich dann sehr einfach die Wärmeleitfähigkeit λ bestimmen. Den Stab und den oberen Teil der Heizplatte isoliere ich natürlich gut gegen Wärmeverluste.
Für das Experiment verwende ich folgende Teile:
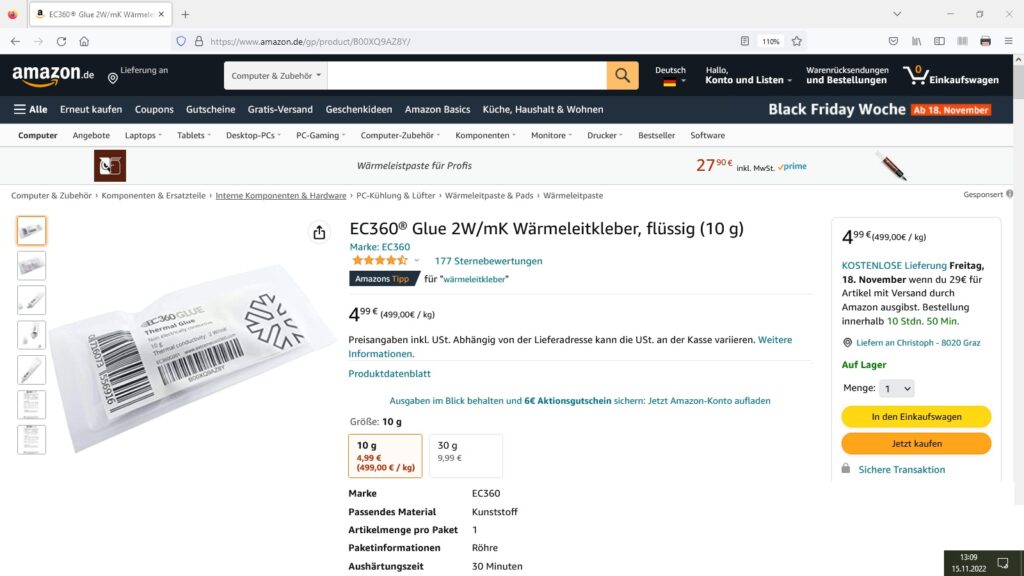
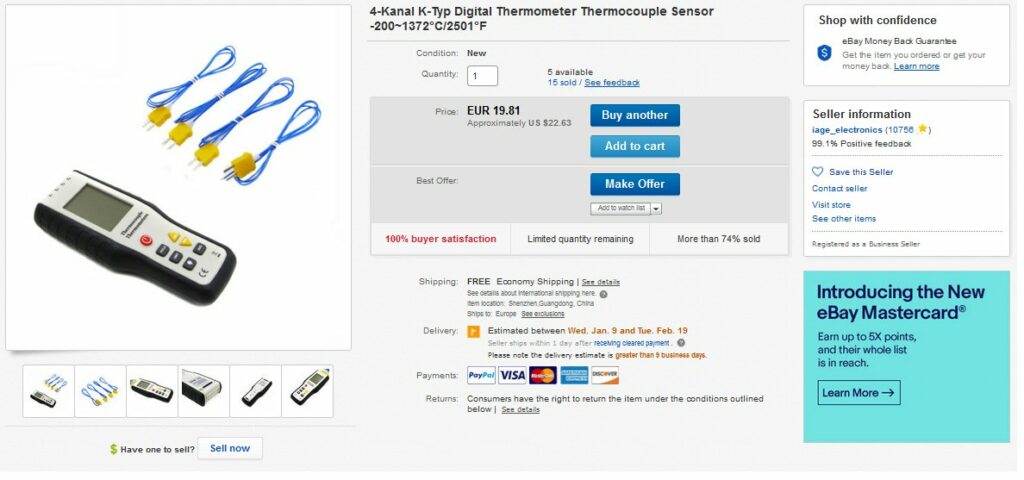

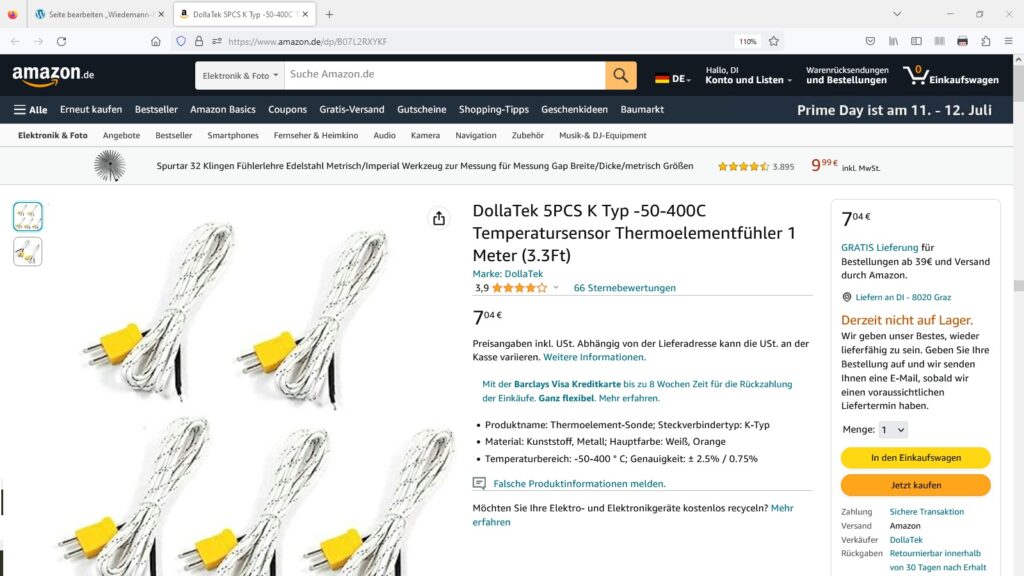
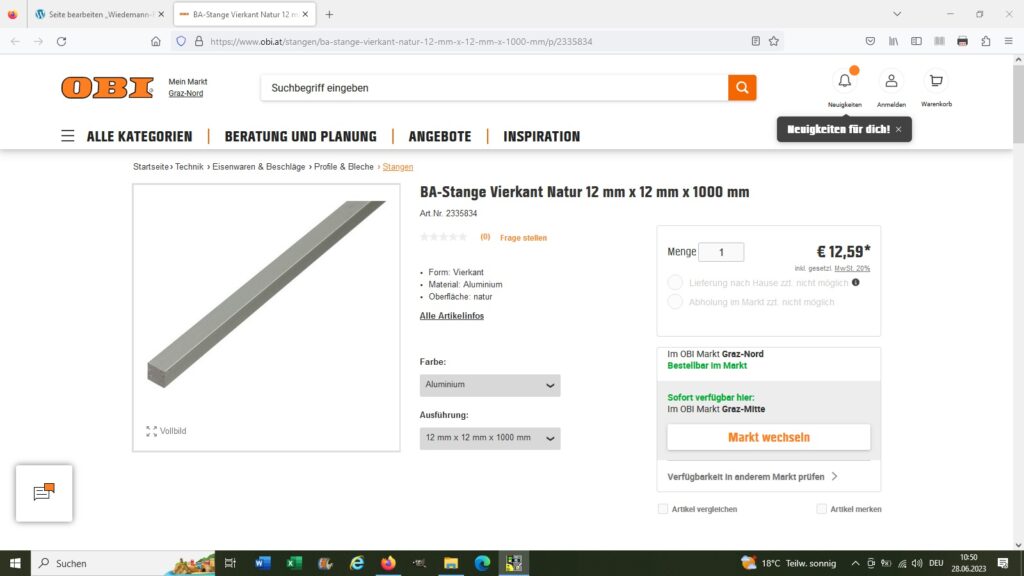
So, ich konnte inzwischen sämtliche Teile im Baumarkt (12 x 12 mm Aluminiumstab und Isolierungsrohr) besorgen bzw. sind diese per Post (Wärmeleitkleber, Heizplatte, K-Type Thermofühler) bei mir eingetroffen.







Den Aluminiumstab habe ich mit reichlich Wärmeleitkleber mit der 12V-Heizplatte verbunden. Die beiden Thermofühler habe ich dann auch noch am Stab mittels Kleber fixiert. Ihr Abstand beträgt 14 cm. Zum Abschluss habe ich dann alles mit dem Isolierrohr bzw. Moosgummi thermisch isoliert.







Bei meinem ersten Versuch habe ich leider eine zu große Heizleistung (9V, 2A) eingestellt. Dabei schmolz mir nicht nur der Moosgummi, auch das experimentelle Ergebnis für die Wärmeleitfähigkeit λ lag mit 516 W/m·K aufgrund der starken Wärmeverluste weit weg vom theoretischen Wert 236 W/m·K für Aluminium. Daher reduzierte ich in mehreren Schritten die Wärmeleistung sukzessive bis hinunter zu 2 V und 0.23 A. Die experimentell ermittelten Wärmeleitfähigkeiten näherten sich dabei immer mehr dem Sollwert an. Bei einer Heizleistung von 0.46 W betrug das Ergebnis für die Wärmeleitfähigkeit 372.7 W/m·K. Damit lag ich nach wie vor deutlich zu hoch. Ob ich mit dieser experimentellen Anordnung noch bessere Resultate erzielen kann, werde ich überprüfen. Gegebenenfalls müsste ich auf einen anderen experimentellen Zugang wechseln, denn die Heizleistung kann ich nicht wirklich weiter senken, um Wärmeverluste (die ja dann experimentell ein zu großes λ bedingen) zu vermeiden.




Hier die Ergebnisse für die Wärmeleitfähigkeit für sinkende zugeführte Wärmeleistungen:
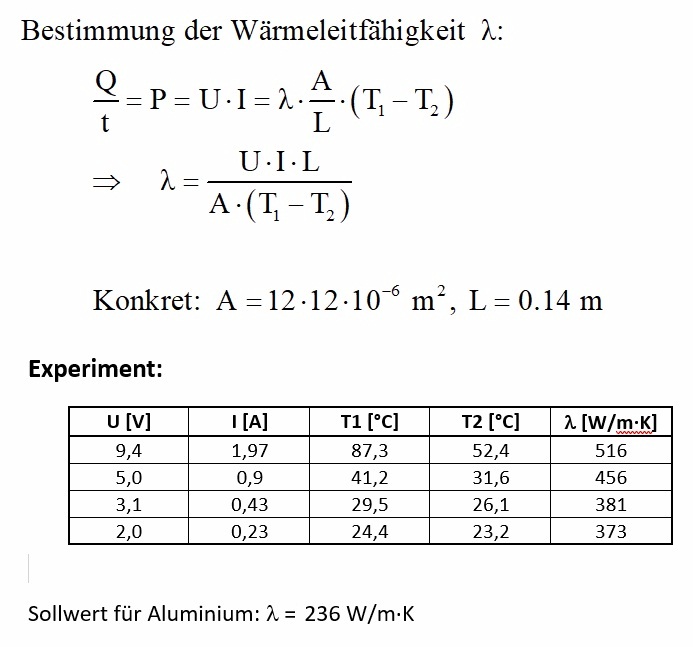
Mittels der ermittelten elektrischen Leitfähigkeit σ und Wärmeleitfähigkeit λ konnte dann schlussendlich das Wiedemann-Franz-Gesetz überprüft werden. Ich erhalte eine Lorenzzahl von 3.43 · 10 ^–8 V²/K². Dieser Wert ist durch die zu große Wärmeleitfähigkeit natürlich auch zu groß. Theoretisch sollte die Lorenzzahl zwischen 2.1 und 2.9 · 10 ^–8 V²/K² liegen.

Vielleicht nehme ich mich ja nochmals der Sache mit der Wärmeleitfähigkeit an. Das Youtube-Video reiche ich wie immer nach…

