Bringt man Materie in ein externes Magnetfeld H, so kann es das Magnetfeld leicht schwächen (diamagnetisch), leicht verstärken (paramagnetisch) oder stark verstärken (ferromagnetisch).
Die magnetische Suszeptibilität χ ist eine dimensionslose Stoffgröße, welche die beiden physikalischen Größen Magnetisierung M und magnetische Feldstärke H miteinander verknüpft.

Die magnetische Suszeptibilität χ kann also leicht negativ (diamagnetisch), leicht positiv (paramagnetisch) oder stark positiv (ferromagnetisch) sein. Reines Vakuum besitzt die relative Permeabilität μr = 1 und demnach die Suszeptibilität χ = μr – 1 = 0. Es kann ja auch ein externes Magnetfeld durch das Fehlen jeglicher Materie auch nicht verändern/verstärken/abschwächen.
In diesem Experiment geht es um die experimentelle Bestimmung der magnetischen Suszeptibilität einer paramagnetischen Flüssigkeit. Ich habe mich für Eisen-III-Chlorid entschieden. Die konkrete Methode zur Bestimmung von χ ist nach dem deutschen Physiker Georg Hermann Quincke benannt.

Bildquelle: https://commons.wikimedia.org/wiki/Category:Georg_Hermann_Quincke?uselang=de#/media/File:Georg_quincke.jpg, public domain
Georg Quincke beschäftigte sich unter anderem mit Fluidmechanik, Oberflächenspannung und eben auch mit magnetischen Eigenschaften von Stoffen. Die nach ihm benannte Quincke-Methode nutzt die Änderung des Flüssigkeitsspiegels in einem engen Rohr (Kapillare) in einem inhomogenen Magnetfeld, um die magnetische Suszeptibilität einer Flüssigkeit zu bestimmen.
Für das starke Magnetfeld werde ich meinen Elektromagneten, welcher schon beim Zeeman-Effekt zum Einsatz kam, verwenden. Dieser liefert magnetische Flussdichten bis ca. 0.44 T.

Wie schon erwähnt steigt der Flüssigkeitsspiegel in der Kapillare geringfügig an, wenn am Ort der Flüssigkeit ein inhomogenes Magnetfeld wirkt. Die Inhomogenität erzeuge ich dadurch, dass zwischen den Polen eine annähernd konstante Flussdichte B herrscht und außerhalb der Pole näherungsweise B ≈ 0 gilt. Die Steighöhe h ist dann direkt proportional zur magnetischen Suszeptibilität:

Eine kurze Überschlagsrechnung liefert selbst bei großen magnetischen Flussdichten um die 0.4 T nur eine Steighöhe von 0.2 mm. Das ist nicht wirklich viel…
Um diesen geringen Hub erfassen zu können, benötigt man ein Mikroskop. Ich werde mein Smartphone in Kombination mit einer Linse eines Lasermoduls verwenden:

Mit der Halterung und einer Klammer kann ich die Linse bequem vor dem Handyobjektiv fixieren:

Zum Kalibrieren meines Mikroskops dient ein Objektträger mit Skala (1 div = 10 µm):


Die mit diesem Setup erzielte Auflösung beträgt 2.235 µm/Pixel:

Das Eisen-III-Chlorid habe ich im Internet bestellt:



Die Kapillare ist über ein U-Rohr mit einem Reservoire mit deutlich größerem Querschnitt verbunden. Damit bleibt der Flüssigkeitsspiegel im Reservoire annähernd konstant und die Steighöhe in der Kapillare ist doppelt so groß verglichen mit keinem Reservoire. Diesen größeren Behälter habe ich mir aus einem Stück Plexiglasrohr gebastelt:


Wie schon angedeutet, kommt bei diesem Experiment mein starker Elektromagnet zum Einsatz:




Der Versuchsaufbau zur Messung der Flussdichte B zwischen den Polen in Abhängigkeit von der Spannung/Stromstärke durch die beiden Spulen:


Für eine Flussdichte von 0.44 Tesla benötigte ich bereits eine Stromstärke von mehr als 15 A bei einer Spannung von 31.7 V. Die elektrische Leistung beträgt dann beachtliche P = U · I = 488 W.

Aus der Steighöhe h kann man nach obiger einfacher Quincke-Formel die magnetische Suszeptibiliät berechnen:

Wie kommt man aber auf diese Formel? Solche Fragen lassen mir in der Regel keine Ruhe. Also habe ich unter anderem auch Chat-Gpt gefragt und dieser hat mir die Formel für die infinitesimale Kraft dF auf eine paramagnetische Flüssigkeit mit dem Volumen dV geliefert:

Chat-GPT hat mir auch gesagt, dass die Quincke-Formel von einer sprunghaften Magnetfeldänderung in z-Richtung ausgeht. Also habe ich mir einen linearen Feldverlauf H(z) gebastelt:

Mit diesem speziellen H(z)-Verlauf bin ich dann in die Formel für die Kraft dF gegangen und habe die Ausdrücke integriert. Der Gradient von H² liefert mittels Kettenregel d/dz H² = 2 · H · dH/dz.

Ich erhalte also mittels meiner eigenen Herleitung (Anm.: Im Internet bin ich leider auf keine zusätzliche Information gestoßen) in der Tat die Quincke-Formel für die magnetische Suszeptibilität χ in Abhängigkeit von der Steighöhe h der paramagnetischen Flüssigkeit, Heureka 🙂
In der Zwischenzeit konnte ich das Experiment durchführen. Zum Glück befand sich ein starker Elektromagnet bereits in meiner Sammlung. Diesen habe ich einst für den Nachweis des Zeeman-Effekts gebastelt. Er liefert magnetische Flussdichten bis zu ca. 0.45 T. Der Aufbau erfolgte wie üblich bei mir in der Küche:




Leider stellte sich heraus, dass ich mit meinem selbstgebauten Smartphone-Mikroskop nicht in den Fokus kam. Der minimale Abstand Objektiv–Rohr war zu groß:

Also musste ich mir eine andere Lösung überlegen. Ich habe ja zum Glück über all die Jahre ein vielfältigstes Instrumentarium angeschafft. Darunter befand sich auch ein kommerzielles Handymikroskop. Um mit diesem wirklich sehr nahe an das Rohr heranzukommen, entfernte ich unnötiges Plastik:




Jetzt passte alles wie erwünscht…

… und ich konnte das Eisen(III)chlorid einfüllen:


Bild meines Smartphones:

Die beiden Spulen des Elektromagneten versorgte ich mit meinem 30V/30A Netzteil:


Bei z.B. 11 A sollte sich eine Flussdichte von B = 0.4 T ergeben.

Bild bei keinem Magnetfeld, also B = 0 T:

Bild bei einem Magnetfeld B = 0.25 T:

Zur Bestimmung der Steighöhe h muss ich natürlich den Abbildungsmaßstab in µm/Pixel kennen. Dazu habe ich den Innen- und Außendurchmesser des Rohrs bestimmt:


Ergebnis: Innendurchmesser = 4 mm, Außendurchmesser = 6 mm.
Für die Berechnung der magnetischen Suszeptibilität χ benötige ich auch noch die Dichte der Flüssigkeit. Diese war mit meiner mg-Waage und einem Pyknometer schnell ermittelt:




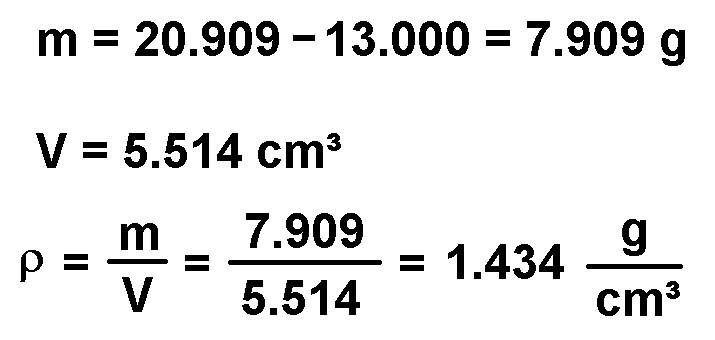
Nochmals die Formel zur Berechnung der magnetischen Suszeptibilität χ:

Ergebnis für B = 0.25 T:

Den Versuch habe ich dann noch für weitere Flussdichten B = 0.3 T und B = 0.36 T wiederholt:

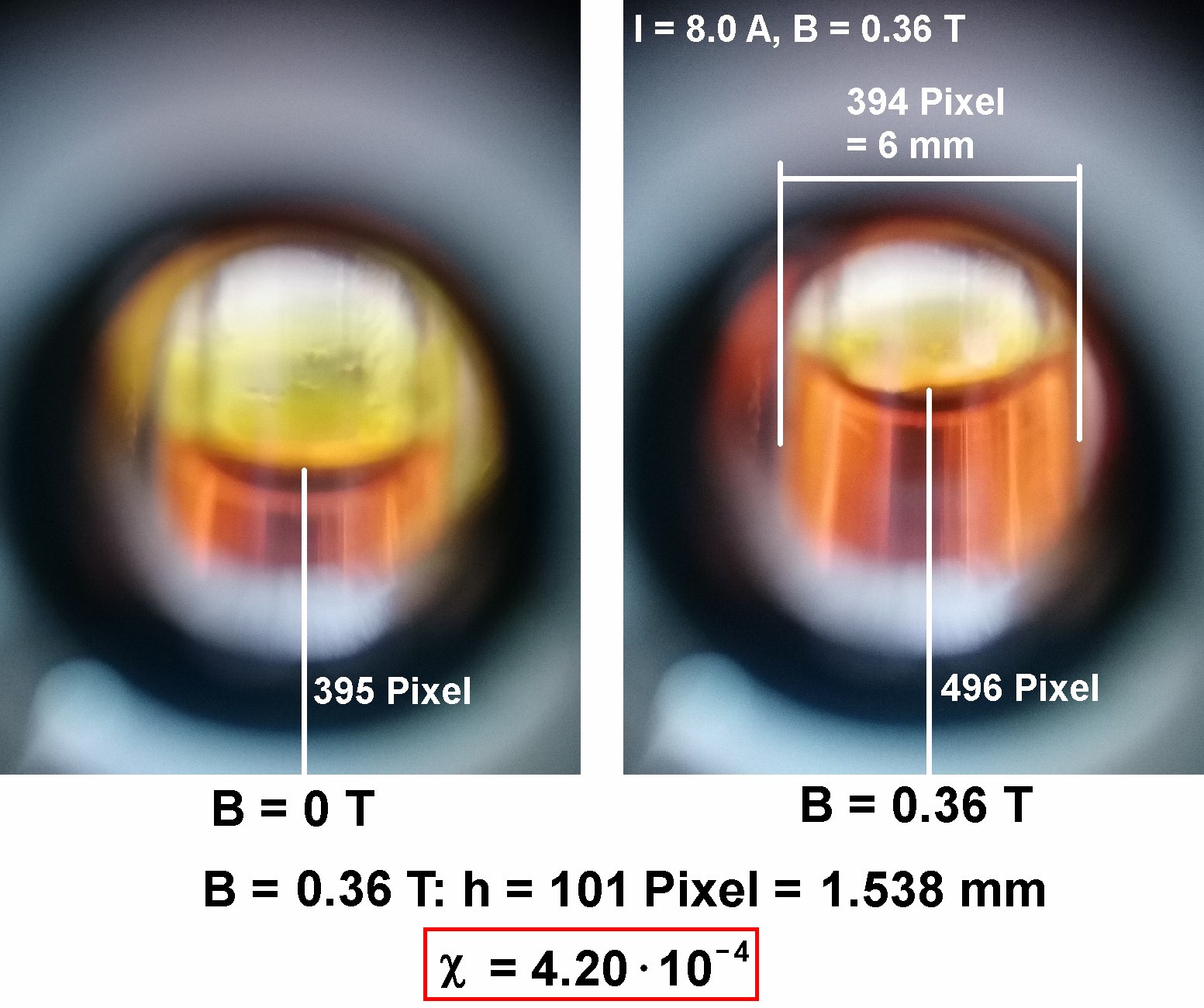
Ich komme also auf Werte im Bereich von χ = 4.6 · 10^ –4. Dies möchte ich natürlich mit dem Sollwert vergleichen. Leider liefert das Internet sehr unterschiedliche Werte für die molare Suszeptibilität von Eisen(III)chlorid. Diese variieren oft um einen Faktor 10! Chat GPT hat mir den Wert χm = 1.7 · 10^ –8 m³/mol genannt:

Damit konnte ich χ berechnen:

Der Sollwert beträgt also χ = 6 · 10^ –5. Dieser Wert ist somit nur ca. 1/8 meines experimentell erhaltenen Werts von χ = 4.6 · 10^ –4. Warum dies so ist, weiß ich im Moment leider nicht. Vielleicht hat ja einer der Leser eine Idee und verfasst einen Homepage-Kommentar 😉

Das Youtube-Video reiche ich wie immer nach…

