Die folgenden Freihandversuche dienen zur Veranschaulichung bzw. zum Nachdenken im Physik-Unterricht und können auch von Schülern ohne Schwierigkeiten durchgeführt werden.
Inspiriert wurde ich unter anderem zu diesen Versuchen von einer schon recht alten (1997), aber für mich immer noch äußerst wertvollen CD mit über 400 Freihandversuchen aus vielen Bereichen der Physik von der Universität Augsburg/Deutschland.
Literatur: Hilscher, H.: Universität Augsburg, Institut für Didaktik der Physik, CD-ROM Freihandexperimente
Bezugsquelle: https://www.isbn.de/buch/9783933446015/physikalische-freihandexperimente

Viel Spaß beim Nachmachen und Experimentieren… 😉
Der magische Doppeltrichter
Dieser aus zwei Trichtern bestehende Körper besitzt sogar die Fähigkeit bergauf zu rollen.






Natürlich kann er dies nur, weil sich sein Schwerpunkt während des Bergauf-Rollens senkt 😉

Einfache Magnetfeldsonde
Zur Veranschaulichung von Magnetfeldern eignet sich diese nur aus einer Büroklammer, etwas Klebeband und einer Schnur bestehende Magnetfeldsonde…

Quelle: Universität Augsburg, Institut für Didaktik der Physik, CD-ROM Freihandexperimente





Die folgsame Garnrolle
Für dieses anschauliche Experiment wird lediglich eine Garnrolle benötigt.

Ihr Verhalten hängt ganz entscheidend vom Winkel α des Seils ab.

Quelle: Universität Augsburg, Institut für Didaktik der Physik, CD-ROM Freihandexperimente
Bei kleinem Winkel α rollt/rotiert die Garnrolle nach rechts:

Bei einem bestimmten Winkel α rollt/rotiert die Garnrolle gar nicht, sondern sie rutscht nur:

Und ist schließlich der Winkel α groß, so rotiert die Garnrolle nach links:

Zu erklären ist dieses Verhalten mit dem wirkenden Drehmoment:

Ganz links im Bild wirkt durch den nach rechts gehenden Hebel r ein nach links wirkendes Drehmoment. Daher rollt/rotiert die Garnrolle in diesem Fall nach links. Im mittleren Bild zielt die Kraft genau auf den Auflagepunkt. Der Hebel r ist nun genau 0 und daher wirkt kein Drehmoment. Die Garnrolle rutscht nur nach rechts. Im rechten Bild zeigt der Hebel nach links und es kommt zu einem nach rechts wirkenden Drehmoment. Die Garnrolle wird in diesem Fall nach rechts rollen/rotieren.
Hier das Video zu diesem Experiment:
Ein Beschleunigungsmesser
Dieses Experiment ist finde ich besonders faszinierend, führt es doch seine Beobachter zunächst in die Irre. Man braucht dazu ein wasserdichtes Glasgefäß mit Schraubdeckel, eine Schnur, Wasser, einen Korken und Heißkleber. Der Aufbau ist sehr simpel:





Die Schnur klebt man zuerst an der Unterseite des Korkens fest und danach an der Innenseite des Deckels. Die Schnurlänge ist dabei so zu wählen, dass der Korken später dann ca. bei 2/3 der Glashöhe schwebt.




Bei der Durchführung des Experiments fragt man zuerst die Schüler, wohin sich der Korken wohl bewegen wird, wenn man das gesamte Glas in eine Richtung beschleunigt. Die allermeisten Kinder werden antworten, dass sich der Korken aufgrund seiner Trägheit in die Gegenrichtung zur Beschleunigung bewegen wird. Führt man dann den Versuch durch, so stellt man verwundert fest, dass sich der Korken genau in die Gegenrichtung, also in Richtung der Beschleunigung bewegt.

Bei einer Kreisbewegung bewegt sich der Korken also nicht nach außen, sondern nach innen! Warum ist dies so? Nun, das Wasser im Glas ist natürlich auch träge. Aufgrund der Beschleunigung wirkt dann auf das Wasser eine Trägheitskraft in die zur Beschleunigung entgegengesetzte Richtung. Dies führt dazu, dass der Wasserdruck entgegen der Beschleunigung wächst. Im Erdschwerefeld mit der Gewichtskraft nach unten wächst der Wasserdruck mit der Tiefe linear an. Hier wächst er durch die Trägheitskraft entgegen der Beschleunigung linear an. Dies hat zur Folge, dass auf beiden Seiten des Korkens nun ein unterschiedlicher Druck herrscht und somit eine (Auftriebs)Kraft in Richtung der Beschleunigung auf den Korken wirkt! Bremst man dann das Glas wieder ab, so drückt es den Korken nicht nach vorne, sondern nach hinten. Die wirkende Beschleunigung zeigt auch nach hinten. Der Korken zeigt also genau die Richtung der wirkenden Beschleunigung an…
Das Dosenrennen
Für dieses Experiment werden zwei gleich schwere und große Lebensmitteldosen und eine schiefe Ebene benötigt. Eine der Dosen soll einen dünnflüssigen Inhalt besitzen (z.B. eine Suppe), während der Inhalt der zweiten Dose dickflüssig/fest sein sollte (z.B. Chili con carne).




Diese beiden unterschiedliche Dosen postiert man auf einer schiefen Ebene und lässt sie zeitgleich los. Die Dose mit dem dünnflüssigen Inhalt rollt schneller runter als jene mit dem festeren Inhalt. In der Ebene angekommen, holt aber die zunächst langsamere Dose wieder auf und überholt ggf. sogar die andere. Warum ist dies so?

Zu Beginn haben beide Dosen dieselbe potentielle Energie Epot = m·g·h. Diese wandelt sich beim Herunterrollen in kinetische Energie um. Dabei muss die kinetische Energie der Rotation (Rotationsenergie Erot = I·ω²/2) und die kinetische Energie der Translation (Ekin = m·v²/2) unterschieden werden. Der dickflüssige/feste Doseninhalt rotiert mit der Dose mit, wohingegen der dünnflüssige Inhalt zum Teil gar nicht an der Rotation teilnimmt. Demzufolge steckt beim festen Inhalt mehr Energie in der Rotationsenergie, sodass für die Translationsenergie weniger übrig bleibt und die Dose langsamer ist. Bei der dünnflüssigen Dose rotiert im Extremfall nur die Dose selbst, der Inhalt nicht. Daher steckt dort weniger Energie in der Rotation, dafür mehr aber in der Translation bzw. Geschwindigkeit. Man kann auch argumentieren, die Dose mit dem festen Inhalt habe ein größeres Trägheitsmoment I als die Dose mit dem dünnflüssigen Inhalt. Größeres I bedeutet aber kleineres v.


In der Ebene kommt der Dose mit dem festeren Inhalt ihre größere Rotationsenergie/ihr größeres Trägheitsmoment zugute. Das Reibungsmoment T aufgrund der Rollreibung der Dosenhülle ist bei beiden Dosen gleich und führt zu einer negativen Winkelbeschleunigung α nach T = I·α. Ist nun das Trägheitsmoment I bei der Dose mit dem festeren Inhalt größer, so resultiert dies in einer kleineren Winkelbeschleunigung. Die feste Dose verliert also weniger schnell an Rotation.
Es spielt aber auch die innere Reibung des Doseninhalts eine Rolle. Bei der dünnflüssigeren Dose reibt der ruhende Inhalt stärker an der Dose als beim mitrotierenden festen Inhalt. Dadurch sind die inneren Reibungsverluste bei der dünnflüssigen Dose größer und sie verliert schneller ihre Energie…
Schwärzer als Schwarz
Eine schwarze Oberfläche absorbiert Licht zu etwa 95%. In diesem Experiment werden wir sehen, dass es aber noch etwas bedeutend dunkleres als Schwarz gibt und zwar ein „schwarzes Loch“. Für diesen Versuch werden nur eine Kaffeetasse (Anmerkung: Deren Innenseite kann auch weiß sein) und ein Stück stärkeres, schwarzes Papier benötigt. In dieses schneidet man ein Loch mit einem Durchmesser von ca. 4 mm aus.



Legt man nun das Papier mit dem Loch auf die Kaffeetasse, so erscheint das Loch deutlich dunkler als das schwarze Papier.

Es scheint also aus dem Loch viel weniger Licht zu kommen als vom schwarzen Papier reflektiert wird. Dies betrachten wir nun genauer:

Das eindringende Licht der Intensität I0 wird an der Innenseite der Tasse gestreut und trifft mit einer Wahrscheinlichkeit p auf das Loch und kann die Tasse somit wieder verlassen. Mit der Wahrscheinlichkeit 1 – p bleibt es aber in der Tasse und wird ein weiteres Mal gestreut. Man kann also folgenden Wahrscheinlichkeitsbaum aufzeichnen:
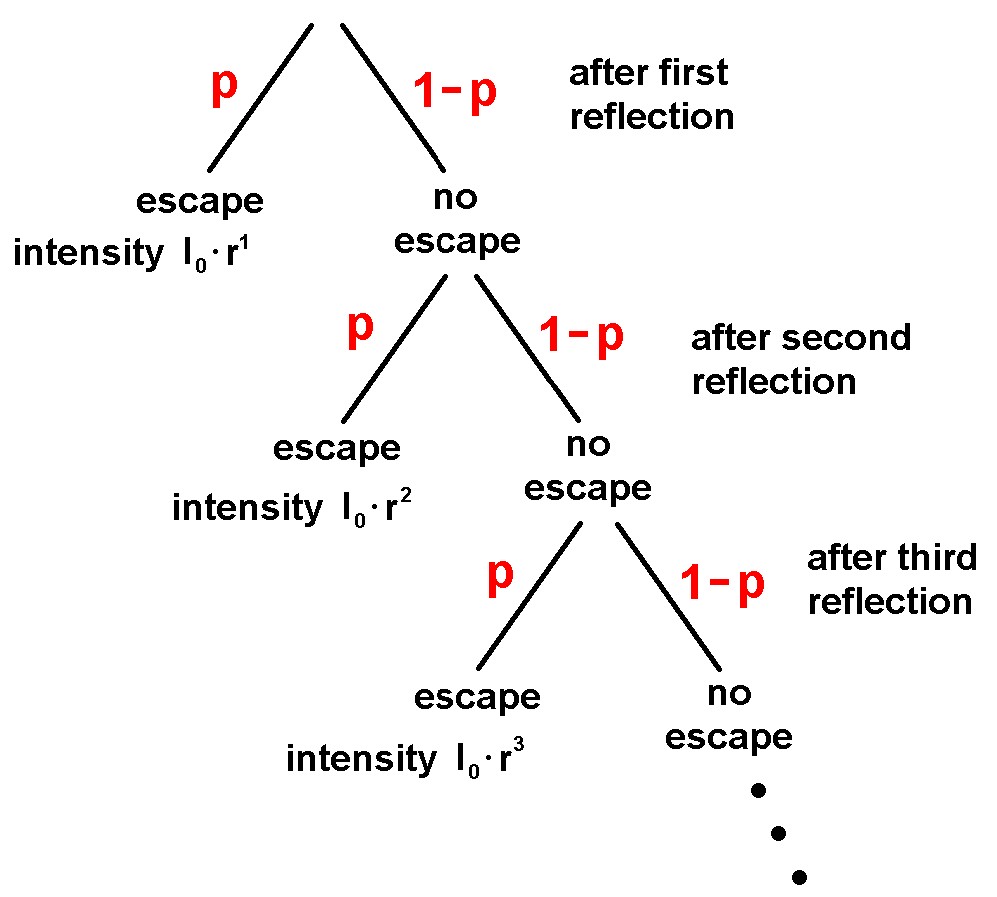
Für die Berechnung der mittleren wieder austretenden Intensität muss man die Einzelwahrscheinlichenkeiten mit den Einzelintensitäten multiplizieren und dann alles aufsummieren:

Man erhält also für die mittlere wieder aus dem Loch tretende Intensität einen Wert von 0.002 · I0, also einen „Reflexionsgrad“ von 0.2%. Schwarze Oberflächen reflektieren zwar das Licht sehr schlecht aber immer noch mit ca. 5%. Wie man sieht, ist der Reflexionsgrad des Lochs deutlich geringer und dieses erscheint demnach verglichen mit dem schwarzen Papier deutlich dunkler/schwärzer…

Nicht-Newtonsche Flüssigkeit
Nicht-Newtonsche Flüssigkeiten sind eine faszinierende Klasse von Flüssigkeiten, die ein einzigartiges Fließverhalten aufweisen und sich dem traditionellen Verständnis der Fluiddynamik widersetzen. Im Gegensatz zu Newtonschen Flüssigkeiten, die einer linearen Beziehung zwischen Scherspannung und Schergeschwindigkeit folgen, weisen nicht-newtonsche Flüssigkeiten komplexe und oft unvorhersehbare Fließeigenschaften auf.

Ein Beispiel für eine solche anormale Flüssigkeit ist Maizena, pure Maisstärke. Diese löst man einfach in Wasser auf. Ich habe dazu 170 g Maizena mit 130 g Wasser vermischt.




Bei langsamen Bewegungen verhält sich die Mischung wie eine Flüssigkeit. So kann man etwa mit einer Zange oder einen anderen Gegenstand bei langsamen Bewegungen in die Mischung eintauchen und sich darin bewegen:

Stößt man mit der Zange aber schnell zu, so verhält sich die Mischung wie ein Festkörper und blockt diese schnelle Bewegung ab:

Kinder/Schüler sind ebenso fasziniert von diesem Verhalten wie ich und sie wollen alle ihren Finger einmal langsam und dann schnell in die Maizena-Wasser-Mischung eintauchen 😉
Der Spritzenwettkampf der Geschlechter
Burschen behaupten ja zumeist das stärkere Geschlecht zu sein. Dieser Auffassung wirkt folgender Versuch entgegen. Man benötigt nur zwei unterschiedlich große (z.B. 5 ml und 20 ml) Spritzen, einen Schlauch und Wasser.




Die beiden Spritzen und den Schlauch füllt man komplett mit Wasser. Eventuell fixiert man den Schlauch auf den beiden Spritzenstutzen noch mit Kabelbinder. Dann wählt man ein vermeintlich schwaches Mädchen und einen männlichen Kraftprotz aus. Ziel ist es, seine Spritze ganz reinzudrücken. Dem Mädchen gibt man die kleine Spritze in die Hand, dem Burschen natürlich die große.
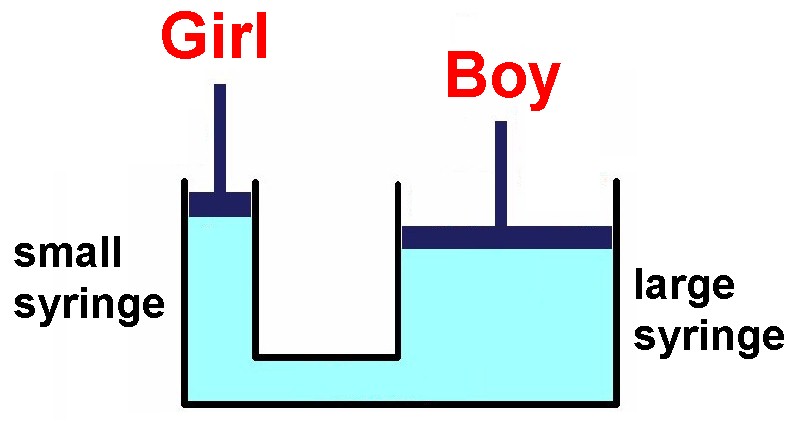
Zur Überraschung aller, gewinnt natürlich das Mädchen. Warum ist dies so? Nun der Druck p im Wasser ist überall gleich. Es gilt daher auch: p = F1 /A1 = F2 / A2. Die Fläche A1 ist aber deutlich kleiner als die Fläche A2. Daher ist die vom Mädchen aufzubringende Kraft F1 auch deutlich geringer als die Kraft F2 des Burschen und sie gewinnt… 😉

Übringens, dies ist auch ein sehr schöner Versuch um zu zeigen, dass man sich bei verminderter Kraft F keine Arbeit erspart. Der beim Reindrücken der kleinen Spritze zurückgelegte Weg s ist nämlich größer und somit die geleistete Arbeit W = F · s gleich.
Gekoppelte Schwingungen
Mit zwei Wäschekluppen und einem breiteren Gummiband lässt sich ein sehr schöner Versuch zum Thema gekoppelte Schwingungen durchführen. Das Gummiband wird auf der Vorrichtung gespannt und dann die beiden Kluppen festgemacht.







Stößt man nun eine der beiden Kluppen an, so beginnt diese zu schwingen. Nach einer Zeit nimmt aber diese Schwingung ab und die andere Kluppe beginnt verstärkt zu schwingen. Schwingt dann die erste Kluppe überhaupt nicht mehr, so besitzt die Schwingung der zweiten Kluppe ein Maximum. Danach hört schön langsam die zweite Kluppe zu schwingen auf und die erste Kluppe schwingt wieder stärker usw.
Betrachtet man die einzelne Schwingung einer Kluppe, so erhält man eine schöne Schwebung. Die Amplitude nimmt periodisch zu und ab und zwar gegengleich zur jeweils anderen Kluppe.

Domino-Brücke
Mit Domino- oder Kaplasteinen lässt sich ein spannender und lehrreicher Versuch durchführen. Meine Kaplasteine konnte ich günstig und gebraucht auf der österreichischen Verkaufsplattform willhaben erstehen.



Um was geht es in diesem Experiment? Mit den Holzsteinen ist eine möglichst überragende Brücke zu konstruieren. Hier kann man durchaus methodisch vorgehen. Betrachten wir zunächst einen einzelnen Stein. Dieser kippt dann, wenn sich dessen Schwerpunkt S außerhalb der Tischkante befindet.

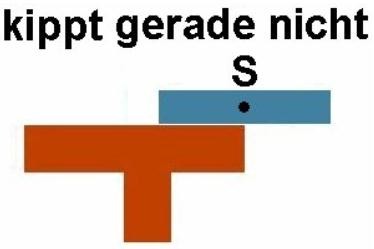

Einen einzelnen Kaplastein kann man also maximal bis zur Hälfte über die Tischkante hinausragen lassen, ohne dass dieser kippt. Der erste Überhang beträgt also L/2 (Steinlänge L).

Fügen wir unterhalb des ersten Steins einen weiteren Kaplastein hinzu, so muss sich dessen Kante also bei L/2 befinden. Beide Steine kann man dann zusammen wieder ein wenig über die Kante schieben und zwar bis zu einem maximalen weiteren Überhang von L/4. Denn dann befindet sich der gemeinsame Schwerpunkt S der beiden Steine genau über der Tischkante:

Kommt ein dritter Stein hinzu, so muss dieser bei L/4 unterhalb des zweiten Steins postiert werden. Zudem kann der dritte Stein bis zu einem Überstand von L/6 wieder hinausgerückt werden. Der Schwerpunkt S12 trägt ja die Masse von 2 Steinen. Der aus S3 (= Schwerpunkt eines Steins) und S12 neu gebildete Gesamtschwerpunkt S ist also doppelt so nah an S12 wie an S3. Dies wird durch eine Strecke 1/3 von L/2 garantiert, denn dann betragen die Abstände von S zu S12 1/3 · L/2 und von S zu S3 2/3 · L/2. Der dritte Überhang beträgt also 1/3 · L/2 = L/6.
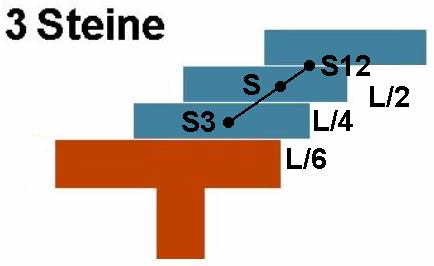
Bei 4 Steinen verläuft die Berechnung analog. Hier beinhaltet der Schwerpunkt S123 die Masse von 3 Steinen und S4 die Masse eines einzelnen Steins. Daher muss der neue Gesamtschwerpunkt S 3-mal so nahe bei S123 sein wie bei S4. Dies schaffen die Abstand 1/4 · L/2 und 3/4 · L/2. Der vierte Überhang beträgt somit 1/4 · L/2 = L/8.

Die Überhänge bilden also eine besondere Zahlenfolge und zwar L/2, L/4, L/6, L/8, L/10 usw. Möchte man den Gesamtüberhang bestimmen, muss man die Einzelüberhänge addieren.

Wir haben es hier also mit einer sog. harmonischen Reihe zu tun. Die einzelnen Glieder 1/i streben zwar gegen 0 (sog. Nullfolge), aber trotzdem divergiert die gesamte harmonische Reihe. Ihre Teilsumme kann mit Hilfe der Näherung ln(n) + 0.57721566 bestimmt werden. Demnach beträgt der gesamte Überhang der Kaplasteine bei insgesamt 10 Steinen (n = 10) 1.44 · L (siehe untere Abbildung). Bei 20 Steinen sind es bereits 1.79 · L und bei 100 Steinen immerhin 2.59 · L. Man benötigt also für einen Zuwachs an Überhang immer mehr zusätzliche Holzsteine, da die Einzelüberhänge abnehmen. Theoretisch kann mit unendlich vielen Kaplasteinen auch ein unendlich großer Überhang konstruiert werden, da eben die harmonische Reihe divergiert 😉

Hier der maximale Überhang gebildet aus 10 Steinen:

Minikartoffelkanone
Gleich vorweg: Im Umgang mit dieser Minikanone ist trotzdem große Vorsicht geraten. Das Gesicht nicht direkt hinter der Dosenöffnung halten und auch ja nicht auf Menschen oder Lebewesen mit Munition im Lauf zielen!
Benötigt werden ein Piezozünder, ein Stück Holz, eine Plastikdose mit verschraubbaren Deckel, ein kurzes Stück dünnen Draht, eine Schraube, Heißkleber und einen Filzstift.







Am Laufende muss man das kurze dünne Drahtstück durch den Lauf stecken und mit Heißkleber fixieren. Dies verhindert dann später, dass die Softgunkugeln in den Innenraum der Dose fallen! Ein kleiner Tipp: Die orangen Filzstifte von Stabilo besitzen genau den richtigen Innendurchmesser für die gelben Softgunkugeln!



Hier sieht man schön den geringen Abstand der Holzschraube zum Drahtende des Piezozünders und den dünnen Draht am Laufende:

Als Treibstoff verwende ich Desinfektionsspray aus Corona-Zeiten:

Die fertige Minikartoffelkanone:

Beim Betätigen des Piezozünders muss die Hand/der Daumen auch die Holzschraube berühren. Nur so ist garantiert, dass innen der Funken überspringt…
Wirbelströme – Zauberkugel
Auch dieses Experiment ist sehr anschaulich und trotzdem sehr einfach. Man benötigt lediglich ein Aluminiumrohr (meines hat einen Aussendurchmesser von 16 mm bei 1 mm Wandstärke) und eine etwas kleinere Magnetkugel bzw. gewöhnliche Stahlkugel. Die Magnetkugel mit einem Durchmesser von 12.7 mm habe ich bei https://www.supermagnete.at/ gekauft.





Lässt man zuerst die Stahlkugel durch das 50 cm lange Aluminiumrohr fallen, so dauert dies nur etwa 0.3 Sekunden. Lässt man danach aber die Zauberkugel (= Magnetkugel) durch das Rohr fallen, so tritt diese erst nach etlichen Sekunden am unteren Rohrende wieder aus. Grund sind die durch den fallenden Magneten induzierten Wirbelströme im Aluminiumrohr. Diese Ströme erzeugen ein zum Magnetfeld der Kugel entgegengesetztes Magnetfeld (also Nordpol auf Nordpol), welches den Fall der Kugel entsprechend verlangsamt. Dieser Versuch eignet sich sehr gut, um die Kinder und Jugendliche zu verblüffen. Schauen doch die beiden Kugeln identisch aus und die Magnetkugel kann durch das nicht magnetische Aluminium auch nicht so leicht entlarvt werden 😉
Roh oder gekocht, das ist hier die Frage…
Einen viel einfacheren Versuch wird es fast nicht geben, denn es werden nur ein rohes und ein hartgekochtes Ei benötigt.

Wie kann man aber sehr einfach und mittels der Physik herausfinden, welches welches ist?
Man versetzt das Ei zunächst in Drehung und stoppt es dann mit dem Finger ab. Nachdem man es wieder loslässt offenbart sich der Unterschied. Während das hartgekochte Ei weiterhin ruhig bleibt, beginnt sich das rohe Ei wieder langsam zu drehen. Warum ist dies so?

Schuld ist die Trägheit. Das Innere des hartgekochten Ei wird durch den Finger komplett zur Ruhe gebracht und verbleibt danach auch in dieser. Das rohe Ei ist aber im Inneren flüssig und träge. Stoppt man das rohe Ei ab, so rotiert das Innere aufgrund der Trägheit noch weiter und versetzt dann das Ei, nachdem man es wieder losgelassen hat, wieder in eine leichte Bewegung 😉
Reaktionszeitmesser
Für dieses simple Experiment zum Thema „freier Fall“ benötigt man nur ein Lineal und eine Skala mit den aufgedruckten Reaktionszeiten.




Der Schüler hält bei der 0-Markierung das Lineal zwischen Daumen und Zeigefinger. Der Lehrer lässt dann irgendwann ohne Vorankündigung das Lineal fallen. Der Schüler hat nun die Aufgabe, das Lineal so schnell wie möglich mit den beiden Fingern zu stoppen. An der Fingerposition kann man dann die Reaktionszeit des Schülers ablesen.

Basis für dieses Experiment ist die Formel s(t) für den freien Fall, welche lautet: s(t) = 1/2 · g · t². Beträgt die Reaktionszeit etwa 0.08 sek, so fällt das Lineal während dieser Zeit um die Strecke s(0.08) = 1/2 · 9.81 · 0.08² = ca. 31.4 mm:

Ist Cola light tatsächlich leichter?


Man nehme ein normales, zuckerhältiges Cola und dann eine Dose Cola light. Legt man beide Dosen ins Wasser so offenbart sich ein Unterschied. Und zwar sinkt das normale Cola zu Boden, während Cola light schwimmt. Warum ist dies so?

Quelle: Universität Augsburg, Institut für Didaktik der Physik, CD-ROM Freihandexperimente
In normalen Cola befindet sich leider eine große Menge Zucker. Dieser gelöste Zucker erhöht die Dichte des Colas deutlich. Dadurch überschreitet die Durchschnittsdichte von Aludose, Luft im Inneren und Getränk jene von Wasser (ca. 1 g/cm³) und dadurch sinkt die normale Coladose zu Boden.
Cola light verwendet zum Süßen stattdessen Süßstoff. Von diesem wird nur eine geringe Menge benötigt. Dadurch steigt die Dichte des Cola lights nur sehr wenig an. Die Durchschnittsdichte der gesamten Dose liegt aufgrunddessen unterhalb von Wasser und die Cola light Dose schwimmt daher an der Oberfläche. Cola light ist also kein Marketing-Gag sondern entspricht ausnahmsweise einmal der Realität 😉
Der gefangene Laserstrahl
Dieses Experiment behandelt das Thema Totalreflexion. Beim Übergang optisch dichtes Medium zu optisch dünnen Medium wird der einfallende Strahl ab einem bestimmten Grenzwinkel (Fall 4 in der nachfolgenden Abbildung) nicht mehr gebrochen, sondern totalreflektiert und kann das Medium nicht mehr verlassen (z.B. Strahl 5).
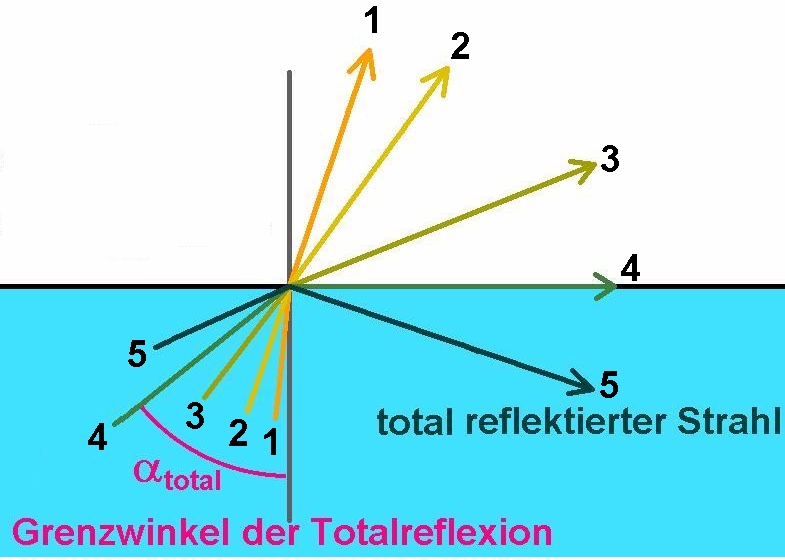
Für diesen Versuch benötigt man lediglich
- einen Laserpointer
- einen Plastikbecher
- ein Tixoband
- Wasser
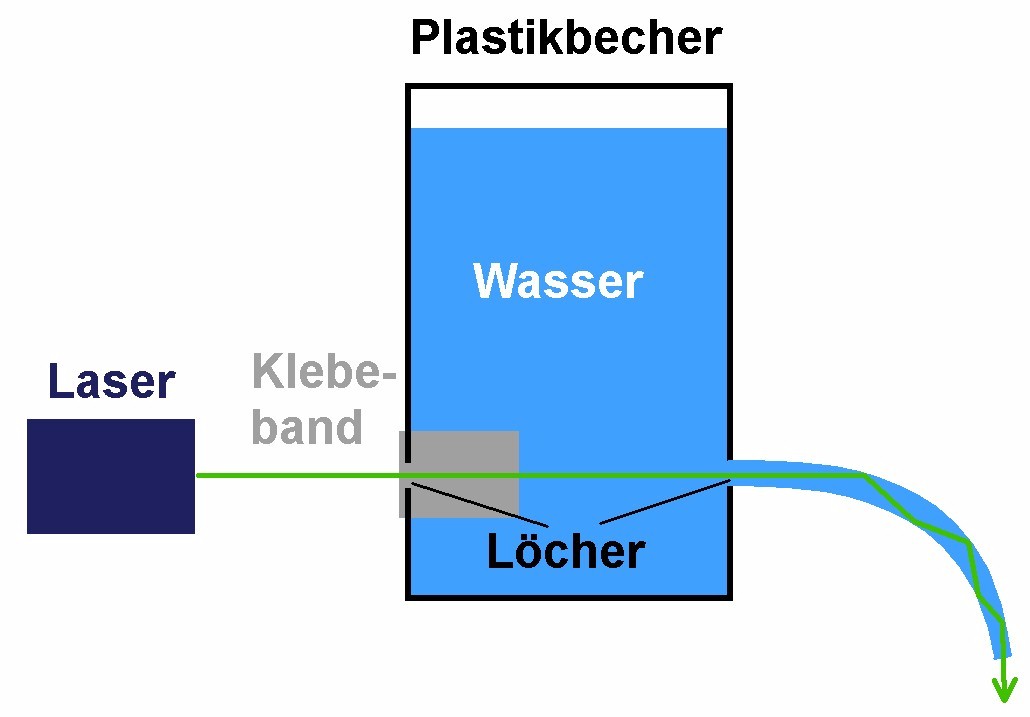
In den Plastikbecher schneidet man genau gegenüber voneinander zwei Löcher:

Eines der beiden Löcher verschließt man wieder mit durchsichtigem Tixoband. Dies wird die Eintrittsöffnung für den Laserstrahl sein…


Aus dem Loch auf der gegenüberliegenden Seite wird dann der Wasserstrahl austreten:







Chaospendel
Chaotische Vorgänge besitzen einen unvorhersehbaren Verlauf und bezeichnend ist auch oft die große Auswirkung von minimalen Veränderungen der Ausgangslage. Schön lässt sich dies mit einem sehr einfachen Chaospendel umsetzen. Man braucht für dieses Experiment nur ein Stativ, einen Faden, 2-3 Ringmagnete, eine M3-Ringschraube und 5 Zylindermagnete.
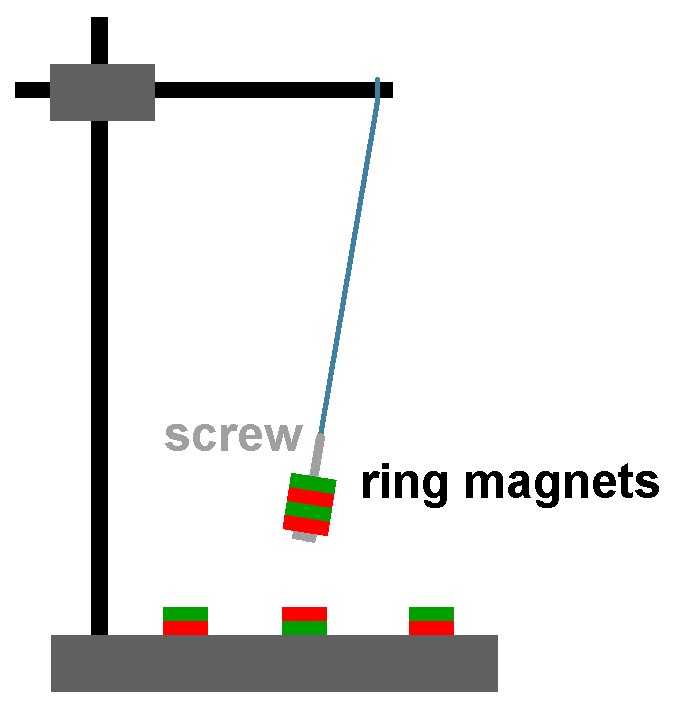

Ich hatte leider nur eine normale M3-Schraube, daher musste ich mittels zweier Lötösen improvisieren. Besser ist natürlich die Verwendung einer Ringschraube…




Bei der Anordnung der Zylindermagnete am Boden unterhalb des Fadenpendels kann man ungezwungen experimentieren. Ich habe es zum Beispiel u.a. mit einem abstoßenden Magneten in der Mitte und 4 anziehenden Magneten rundherum probiert.


Das eisgekühlte randvolle Getränk
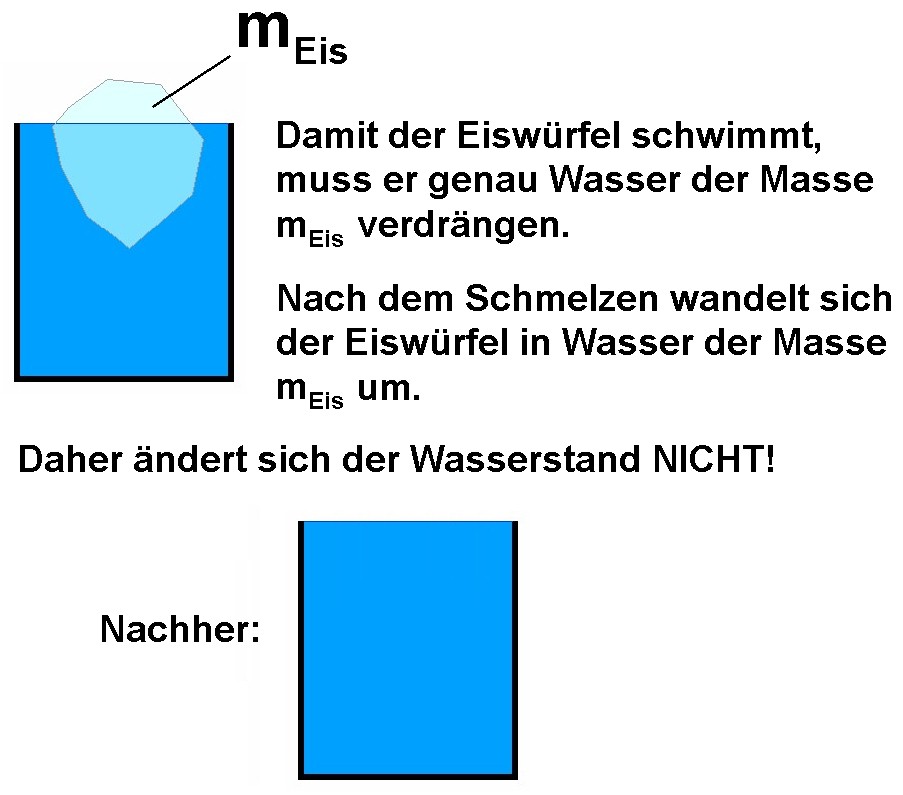
Im Sommer bereitet man sein Lieblingsgetränk oft eisgekühlt zu. Eis besitzt ja eigenartigerweise eine geringere Dichte/größeres Volumen als Wasser. Angenommen es befindet sich im Getränk ein Eiswürfel und das Getränk wurde bis zum oberen Rand eingefüllt.
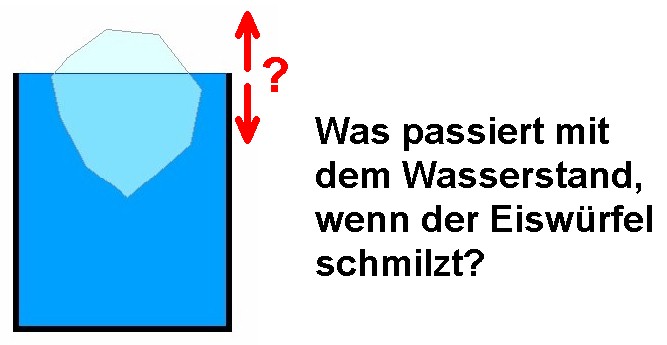
Was passiert nun mit dem Wasserstand, wenn der Eiswürfel schmilzt? Bleibt dieser gleich, sinkt er oder geht das Getränk über? Vor dem Runterscrollen überlege dir selbst die Lösung!
Hier die Auflösung:





Die Erklärung:
Das Glühbirnenrätsel
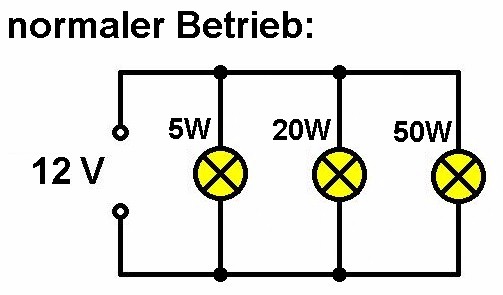
Die Verbraucher im Haushalt sind alle parallel ans 230V-Netz angebunden, damit auch wirklich jeder Verbraucher diesselbe Spannung sieht. Diesen Versuch führen wir aber mit 12V Halogenlampen durch, damit wir die Gefahr der 230V umgehen.
Die Halogenlampen erhält man noch alle im Baumarkt oder Elektronikladen:


Das 50W-Modell:
Dieses besitzt durch die größte Leistung den geringsten Widerstand, sprich die Glühwendel muss am dicksten sein!

Die 20W-Lampe:


Und zuletzt die 5W-Halogenlampe mit der dünnsten Glühwendel:

Schließt man alle drei Lampen parallel an 12V, so strahlt die 50W Lampe wie zu erwarten war am hellsten und die 5W Birne am schwächsten:


Doch was passiert, wenn man alle 3 Lampen in Serie verschaltet und an 12V anschließt? Überlege dir eine Lösung, bevor du weiterliest…


Es leuchtet nur noch eine Lampe und zwar die 5W-Birne:

Warum ist dies so? Nun bei einer Serienschaltung fließt ja durch alle Verbraucher derselbe Strom. Die einzelnen Spannungsabfälle U = I·R sind dann proportional zum Widerstand. Die 5W Glühbirne besitzt mit Abstand den höchsten Widerstand und demnach fällt an ihr auch die größte Spannung ab. Daher leuchtet sie als einzige der drei Halogenlampen, da die an ihr umgesetzte elektrische Leistung am größten ist. Dies lässt sich auch rechnerisch überprüfen:

Ein tolles Rätsel zum Thema Glühbirnen hätte ich noch:
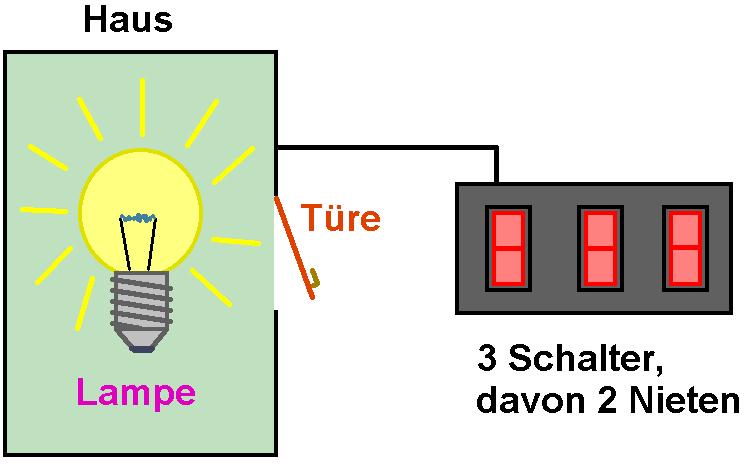
In einem Raum ohne Fenster und nur mit einer Türe befindet sich eine einzelne Glühlampe und ausserhalb des Raums ein Pult mit 3 Schaltern. Zwei davon sind Nieten und nur ein Schalter bedient die Lampe im Inneren des Raums. Wie kann man nun herausfinden, welcher Schalter der Richtige ist? Man darf nur ein einziges Mal den Raum betreten und man sieht auch von außen nicht in den Raum hinein!
Hier die Lösung:
Zuerst betätigt man z.B. Schalter 1 für rund 1 Minute. Danach schaltet man dieses wieder aus und betätigt Schalter 2. Dann geht man in den Raum hinein. Brennt das Licht, so weiß man, dass Schalter 2 der Richtige war. Greift man die Glühbirne an und sie ist noch heiß, war es Schalter 1. Und ist es dunkel und die Glühbirne kalt, so ist Schalter 3 der Richtige. 😉
Kohärer-Effekt
Auch dieser faszinierende Versuch bedarf zur Durchführung nur weniger Teile und zwar einen Plastikbecher, Alufolie, ein Stabfeuerzeug, ein regelbares Netzgerät oder zwei 1.5 V Batterien und eine LED. Zur Erklärung des Effekts verweise ich auf https://de.wikipedia.org/wiki/Koh%C3%A4rer. Nur so viel: Mittels elektromagnetischer Wellen wird eine zunächst nichtleitende Strecke bestehend aus Alukugeln oder Metallspänen leitfähig.
Der schematische Versuchsaufbau und der einfache Zusammenbau:







Zur Durchführung: Zunächst muss man ggf. durch Schütteln dafür sorgen, dass die LED nicht leuchtet, sprich keine leitfähige Verbindung über die Aluminiumbälle gegeben ist. Dann hält man das Stabfeuerzeug über den Becher und betätigt den Zünder. Danach sollte die LED leuchten. Sie leuchtet aber nicht durch etwaige Erschütterungen, sondern durch die beim Zünden des Funkens erzeugte elektromagnetische Welle. Faszinierend 😉
Leidenfrost-Effekt

Quelle: https://de.wikipedia.org/wiki/Johann_Gottlob_Leidenfrost#/media/Datei:Johann_Gottlob_Leidenfrost2.jpg, public domain
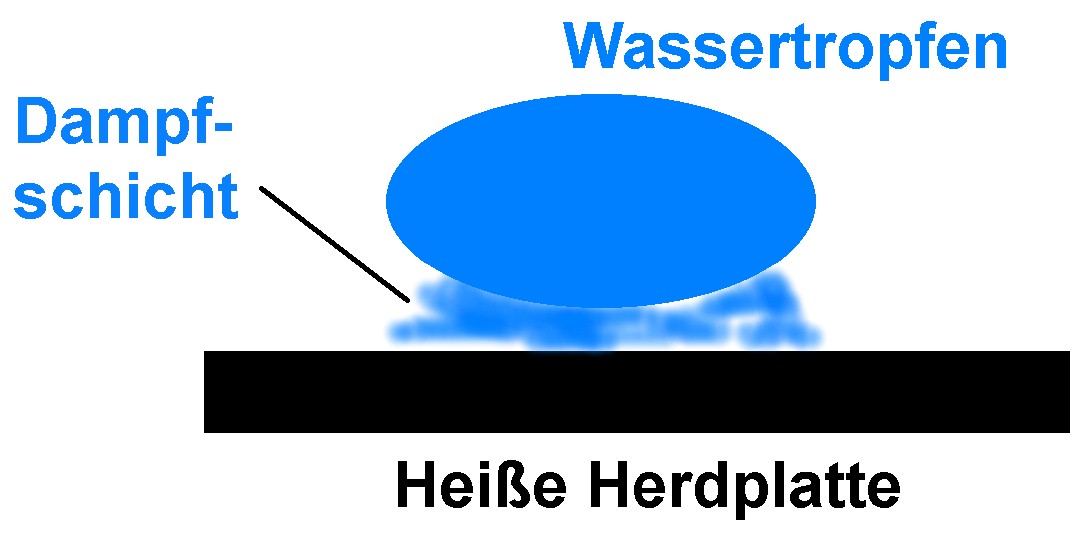
Der Leidenfrost-Effekt, auch Leidenfrost-Phänomen, ist ein von Johann Gottlob Leidenfrost beschriebener Effekt von auf heißem Untergrund springenden („tanzenden“) Wassertropfen. Die Wassertropfen auf z.B. einer Herdplatte „überleben“ recht lange, da sich zwischen ihnen und der heißen Platte eine wärmeisolierende Dampfschicht bildet. Dadurch fließt nur ein relativ geringer Wärmestrom und der Wassertropfen verdampft nicht sofort.
Für diesen Versuch benötigt man nur eine Herdplatte, Wasser und eine Pipette. Die Herdplatte habe ich sehr günstig auf Amazon gekauft:




Der gesamte Versuchsaufbau:

Hier einige Tropfenbilder:





Übrigens, der Leidenfrost-Effekt bewahrt uns auch vor „Verbrennungen“, wenn wir etwa flüssigen Stickstoff mit –196°C auf unsere Hand tröpfeln. Dann ist quasi unsere Hand die heiße Herdplatte…
Kugelrutsche
Für folgendes Experiment wird nur ein großer Gymnastikball und eine Metallkugel benötigt. Die Durchführung ist auch extrem simpel: Man postiert die Metallkugel am höchsten Punkt des Gymnastikballs und lässt diese dann los. Wenn man Pech hat, bleibt die Kugel in ihrem labilen Gleichgewicht ruhen. Im Normalfall wird sie aber runterrollen…

Die Frage ist nun, wann die Kugel den Gymnastikball verlässt. Zur theoretischen Berechnung führen wir den Positionswinkel α ein:
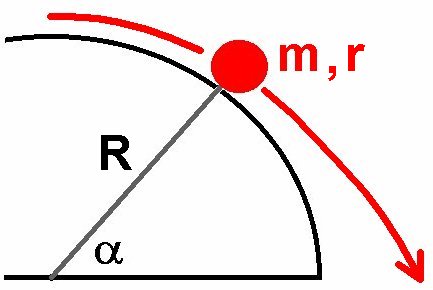
Mit abnehmendem α nimmt die Geschwindigkeit v der Kugel zu, da sie potentielle Energie in kinetische Energie eintauscht. Die Zentrifugalkraft nimmt also immer mehr zu. Die aufgrund des Gewichts nach innen gerichtete Kraft nimmt aber immer mehr ab. Die Kugel verlässt dann den Gymnastikball, wenn die Zentrifugalkraft diese nach innen gerichtete Kraft übersteigt.

Ohne Berücksichtigung der Rotationsenergie der hinabrollenden Metallkugel sollte diese also den Gymnastikball bei einem Positionswinkel von α = 41.8° verlassen. Berücksichtigt man die Rotationsenergie der Metallkugel, so fließt die abnehmende potentielle Energie in die Translation + Rotation. Für die Translationsenergie 1/2 · m · v² bleibt somit weniger übrig als noch in obiger Berechnung. Die Geschwindigkeit v ist nun also bei einem bestimmten Positionswinkel α kleiner als im ersten Fall. Demzufolge ist auch die Zentrifugalkraft geringer und die beiden Kräfte gleichen sich erst bei einem geringeren α aus. Die Metallkugel sollte bei Berücksichtigung der Rotationsenergie den Gymnastikball also erst später verlassen, konkret bei 36°…
Es gilt:
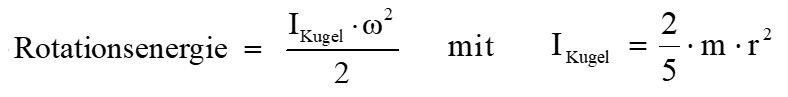

Gymnastikbälle erhält man z.B. günstig auf Amazon:

Metallkugeln habe ich noch in meinem Fundus:

Um den Ablösepunkt der Kugel zu ermitteln schweben mir zwei Varianten vor: Erstens könnte man die Metallkugel etwa mit Tinte einfärben und hinunterrollen lassen. Die Tintenspur würde dann dort enden, wo die Metallkugel den Kontakt zum Gymnastikball verliert. Zweitens kann man den Rollvorgang mit einer Kamera aufzeichnen. Wenn diese senkrecht auf die Bewegung der Kugel blickt, so kann man (hoffentlich) einigermaßen gut erkennen, wann die Kugel den Ball nicht mehr berührt. Zur Auswertung der Einzelbilder des Videos verwende ich wie so oft die Software Tracker (https://physlets.org/tracker/).
In der Zwischenzeit habe ich einen Gymnastikball besorgt und so konnte ich das Experiment durchführen.



Hier die entscheidenden Momente, man erkennt gut, wie die Metallkugel die Oberfläche des Gymnastikballs verlässt:

In der Software Tracker kann wenn der Koordinatenursprung festgelegt wurde u.a. auch der Positionswinkel angegeben werden.
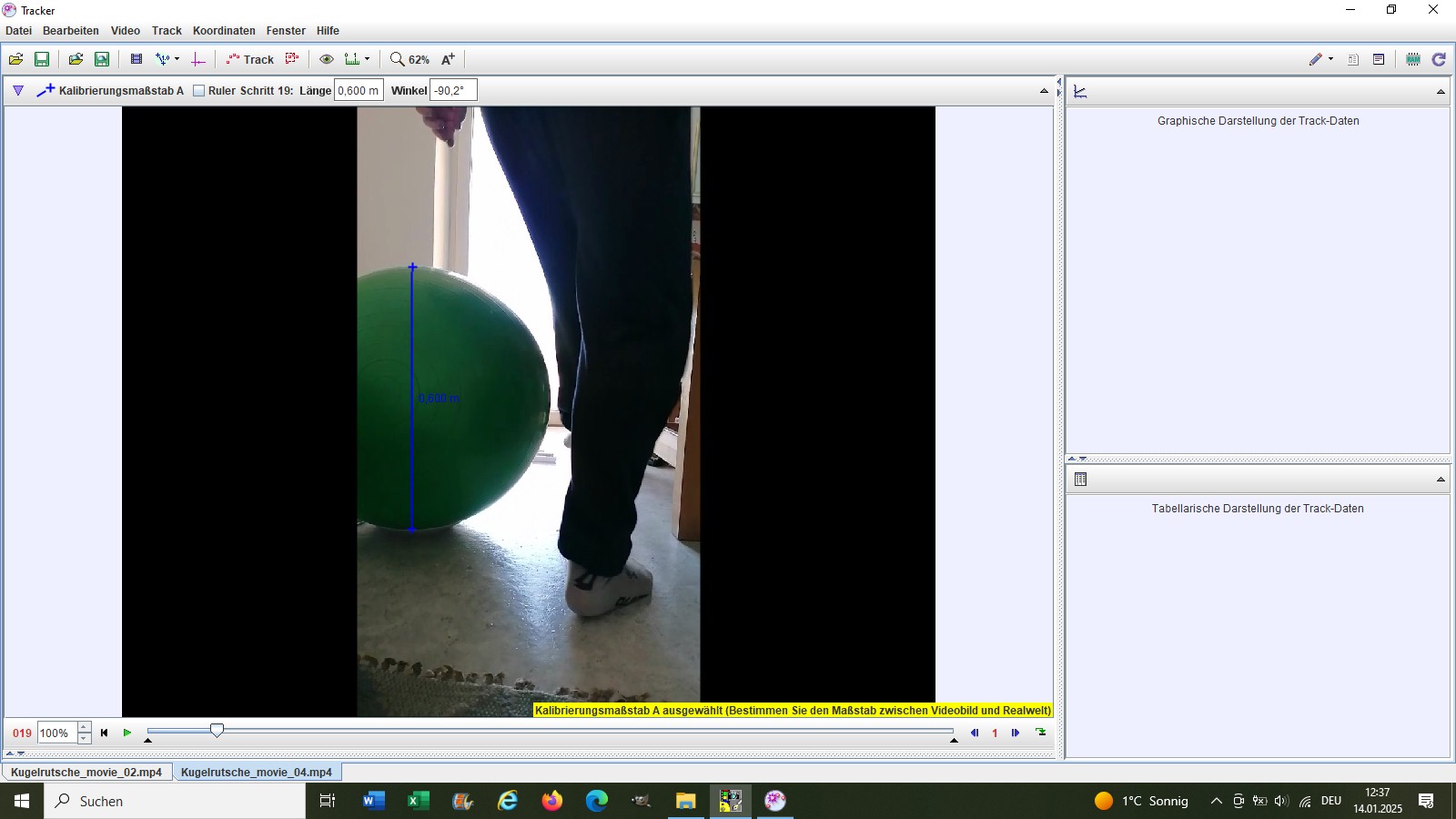
Hier schlängel ich mich bei laufendem Video grazil um den Gymnastikball herum 😉
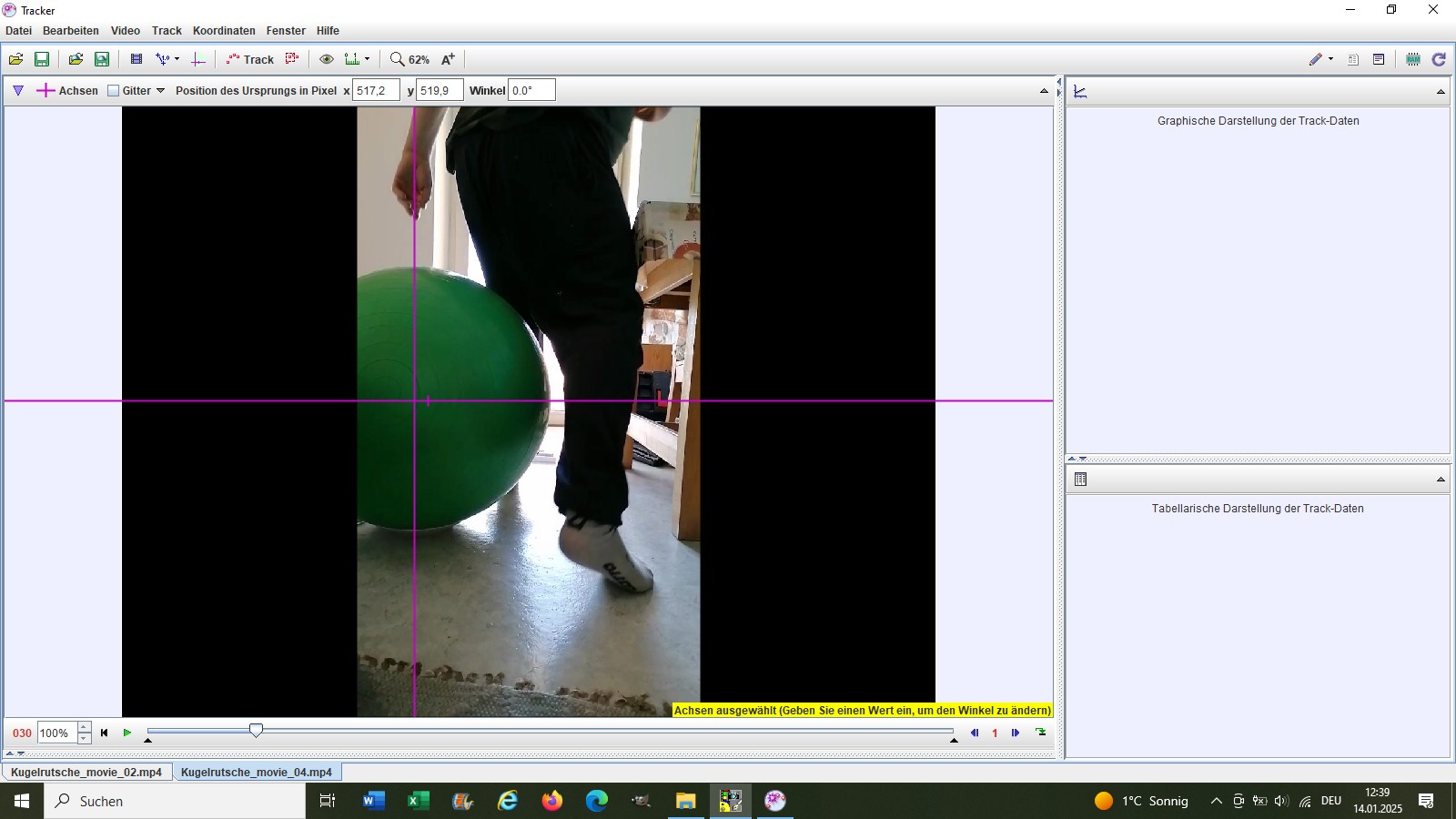
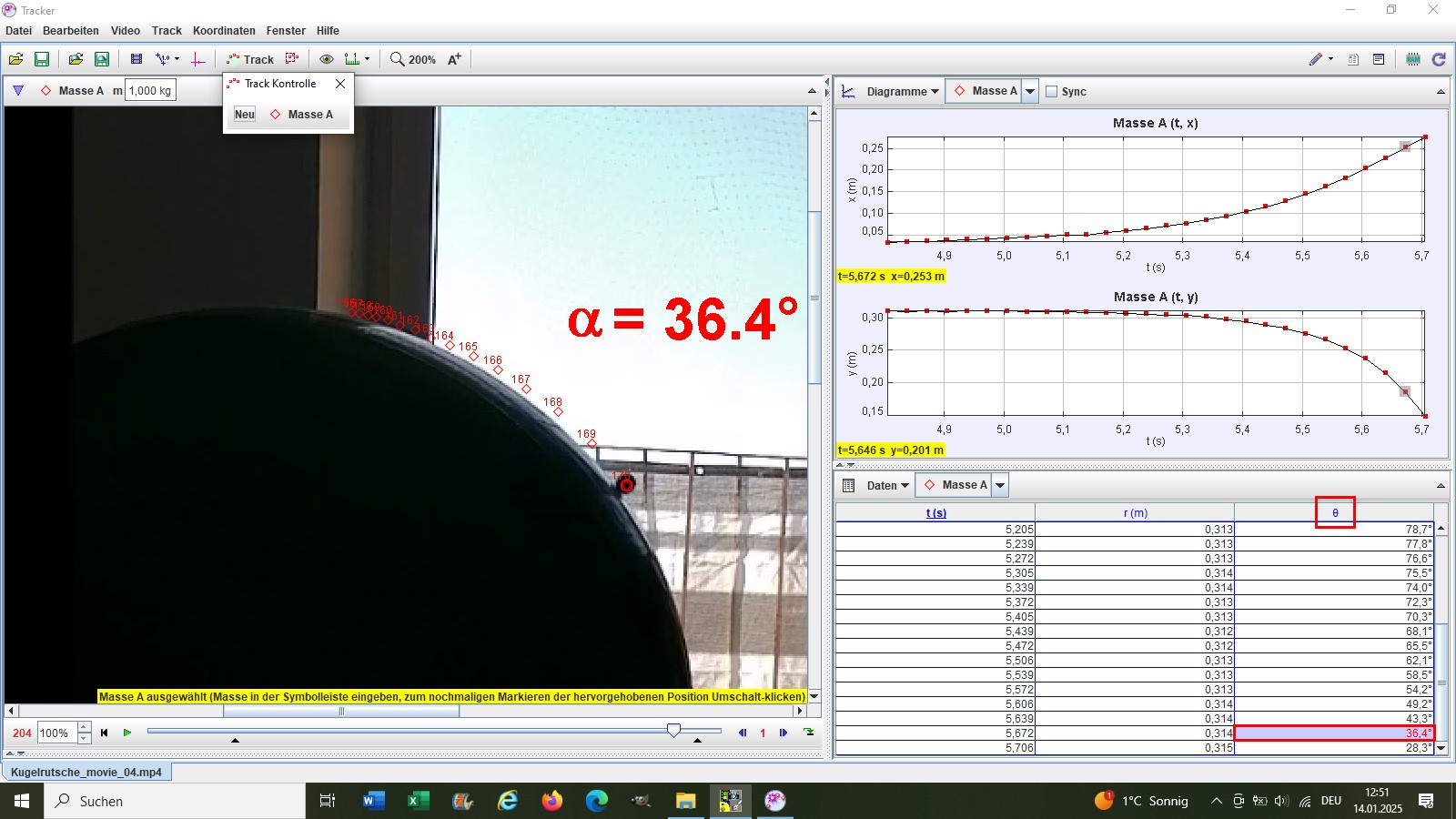
Laut Videoanalyse beträgt der Ablösewinkel α = 36.4°. Dieser Wert deckt sich extrem gut mit der Theorie, Heureka…
Curie-Temperatur
Die materialspezifische Curie-Temperatur TC benannt nach Pierre Curie (1859 – 1906) bezeichnet jene Temperatur, bei deren Erreichen ferromagnetische Eigenschaften eines Materials vollständig verschwunden sind, so dass sie oberhalb nur noch paramagnetisch auftreten.

Bildquelle: https://de.wikipedia.org/wiki/Pierre_Curie#/media/Datei:PierreCurie.jpg, public domain
Den Verlust ferromagnetischer Eigenschaften bei Temperaturen über der Curietemperatur kann man wiefolgt graphisch darstellen:
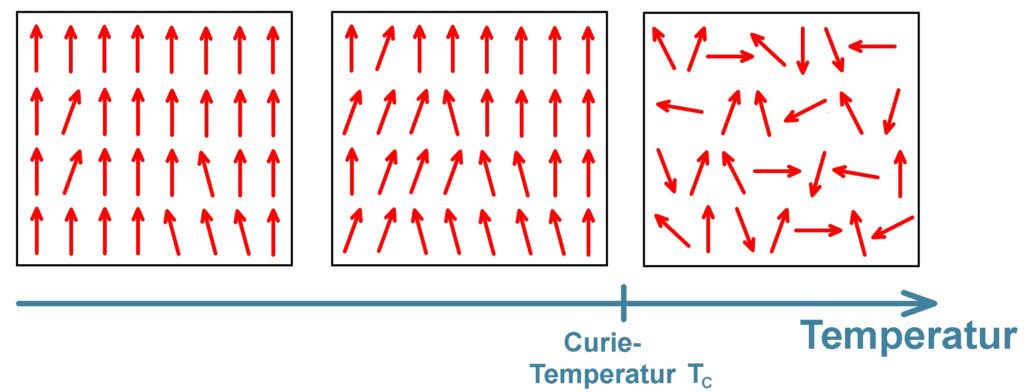
Zunächst sind die Weißschen Bezirke des ferromagnetischen Materials noch weitgehend gleich ausgerichtet. Mit zunehmender Temperatur geraten aber die Atome in immer stärker werdenden Schwingungen bzw. Bewegung. Diese regellose thermische Bewegung wirkt der homogenen magnetischen Orientierung immer mehr entgegen. Oberhalb von TC ist diese Ordnung komplett zerstört und dadurch verschwindet die nach außen wirksame Magnetisierung des Körpers. Er fungiert dann nicht mehr selbst als Magnet…
Diesen Umstand macht man sich bei folgenden beiden Experimenten zunutze. Beim ersten Versuch hängt man einen Eisenstab an einen Kupferdraht. Den Eisenstab habe ich konkret in einem alten DVD-Brenner gefunden.


Den dünnen Kupferdraht binde ich an der Schraube einer Lüsterklemme fest:

Als Magent kommt ein 12 mm messender Würfelmagnet zum Einsatz:

Skizze des gesamten Aufbaus:
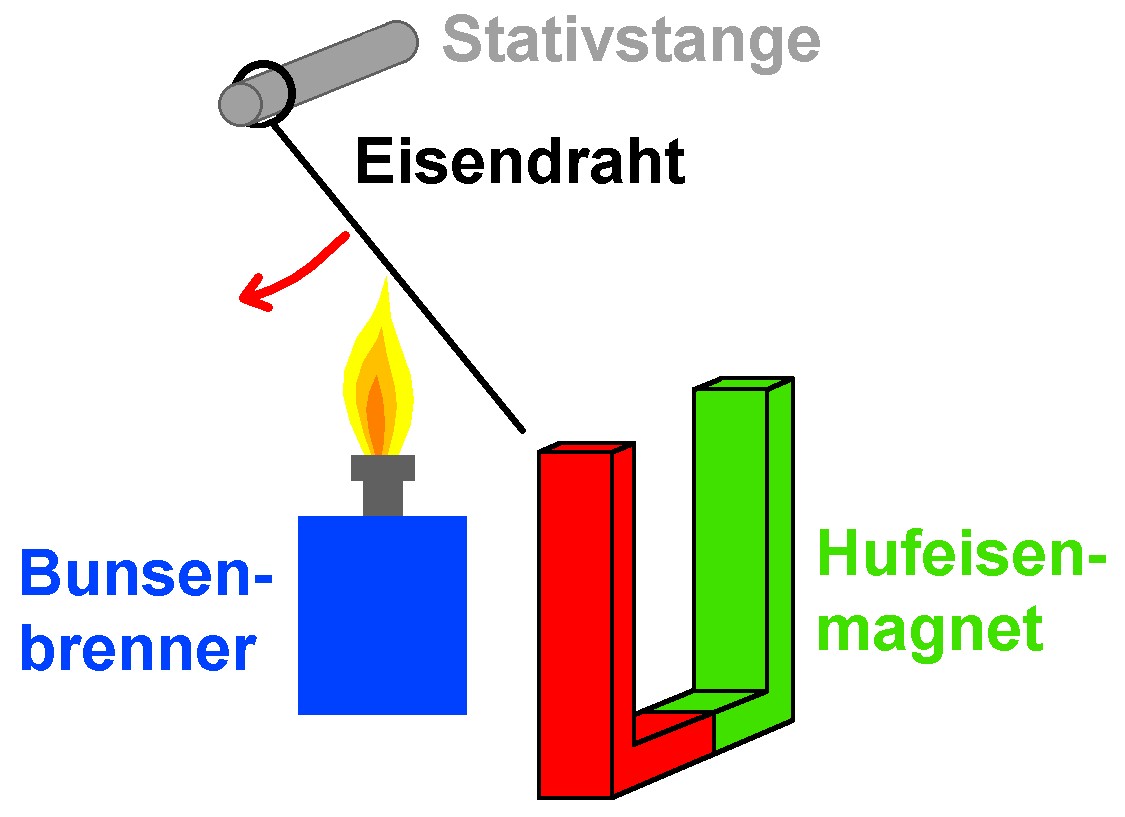
Um den Eisenstab auf eine hohe Temperatur zu erhitzen benötigt man einen Bunsenbrenner oder so wie ich einen Flambierbrenner:


Den Eisenstab hängt man so am Stativ auf, dass er vom Magneten zur Seite abgelenkt wird, diesen aber nicht berührt:

Nun erhitzt man den unteren Teil des Eisenstabs mit dem Gasbrenner…

Hier erkennt man bereits die rötliche Verfärbung des erhitzten Stabendes:

Wenig später verlor der Stab dann seine ferromagnetischen Eigenschaften, seine Magnetpole verschwanden und er wurde vom Magneten nicht mehr angezogen. Infolgedessen pendelte er vom Magneten weg…

Für den zweiten Versuch benötigen wir eine 1 Euro-Münze, konkret nur ihren inneren, silbernen Teil. Dieser besteht nämlich teilweise aus Nickel. Mittels dreier weiterer Münzen baute ich zunächst eine Auflage. Dann schlug ich mit einem Hammer mehrmals kräftig auf einen Alustab, dessen unteres Ende den inneren Teil der Münze (sog. Pille oder Kern) fast vollständig bedeckte. Auf diese Weise kann die Pille vom Ring (= äußerer Teil der Münze) getrennt werden…



In den inneren Teil bohrt man ein kleines Loch für die spätere Aufhängung:

Skizze des gesamten Aufbaus:
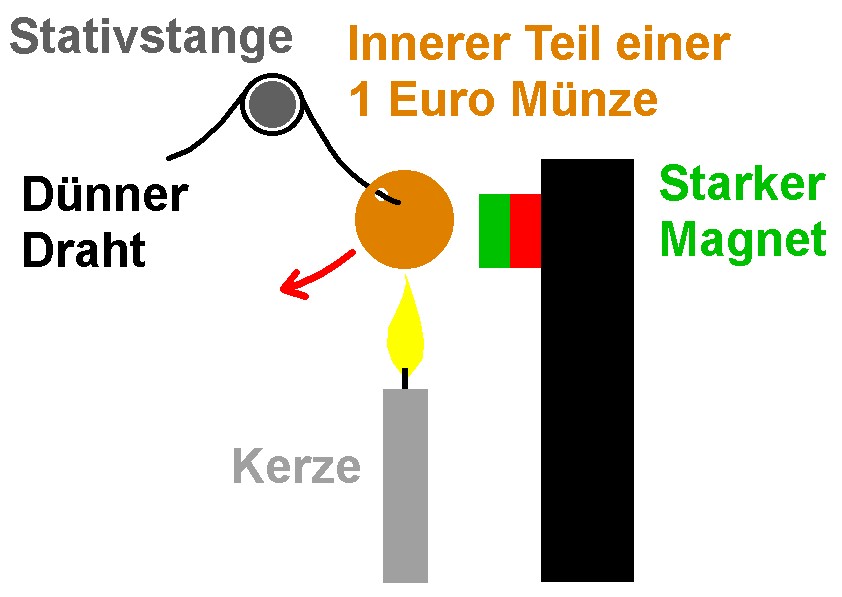
Nun ist etwas Geschick vonnöten und zwar muss der Magnet so positioniert werden, dass er die Münze anzieht aber nicht berührt:


Jetzt kommt die Kerze hinzu: Deren Flamme soll die Münze in der angezogenen Position stark erhitzen. Dadurch verliert die Münze wieder ihre ferromagnetischen Eigenschaften und entfernt sich vom Magneten.


Sie darf nun nicht mehr der Flamme ausgesetzt sein aber auch nicht zu weit vom Magneten entfernt sein, denn dann wird sie im abgekühlten Zustand später nicht mehr vom Magneten wieder angezogen…
Hat man alles richtig gemacht, wird die Münze angezogen, erhitzt sich durch die Flamme über die Curietemperatur, schwingt wieder zurück, kühlt neben der Flamme ab, gewinnt wieder ferromagnetische Eigenschaften und wird dadurch erneut vom Magneten angezogen. Eine ganze Periode kann dabei durchaus eine halbe Minute oder mehr dauern.
Noch ein kleiner Tipp: Anstelle eines Fadens (dieser würde wohl die hohen Temperaturen ohnedies nicht überstehen) verwendet man zur Aufhängung der Münze am besten einen dünnen Kupferdraht, welcher noch eine gewisse Steifigkeit besitzt. Dadurch pendelt die Münze dann nicht zu weit vom Magneten weg und kann dann in weiterer Folge durch die relative Nähe wieder angezogen werden!
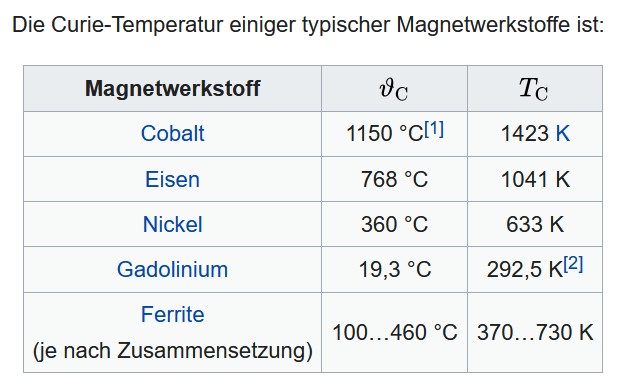
Quelle: Wikipedia
Zum Schluss noch ein Video dieser „Schwingung“:
Hertzscher Dipol – Antenne – elektromagnetische Wellen
Mit diesem sehr einfachen Versuch kann man elektromagnetische Wellen erzeugen, welche sich von einer Antenne loslösen und die mit einer gleichen Antenne wieder detektiert werden können.

Bildquelle: Von Robert Krewaldt, Kaiserplatz 16, Bonn – Cabinetphotograph, Kabinettfotografie, Gemeinfrei, https://commons.wikimedia.org/w/index.php?curid=26781773
Die ersten Experimente mit Radiowellen unternahm der deutsche Physiker Heinrich Hertz. Nach ihm ist die Einheit der Frequenz benannt, wobei gilt 1 Hz = 1 Schwingung pro Sekunde. In einer Stabantenne (= Hertzscher Dipol) schwingen die Elektronen von einem Ende zum anderen. Befindet sich an einem Antennenende ein Elektronenüberschuss (negative Ladung) und am anderen Ende ein Elektronenmangel (positive Ladung), so baut sich ein elektrisches Feld auf. Bewegen sich die Elektronen in der Antenne, so erzeugt dieser Strom ein Magnetfeld. Schwingen nun die Elektronen sehr schnell, so bauen sich elektrisches und magnetisches Feld nicht mehr zurück, sondern sie werden in den Raum abgestrahlt:

Es kommt zu einer elektromagnetischen Welle, in der der E-Vektor normal auf den B-Vektor steht und beide phasengleich sind:
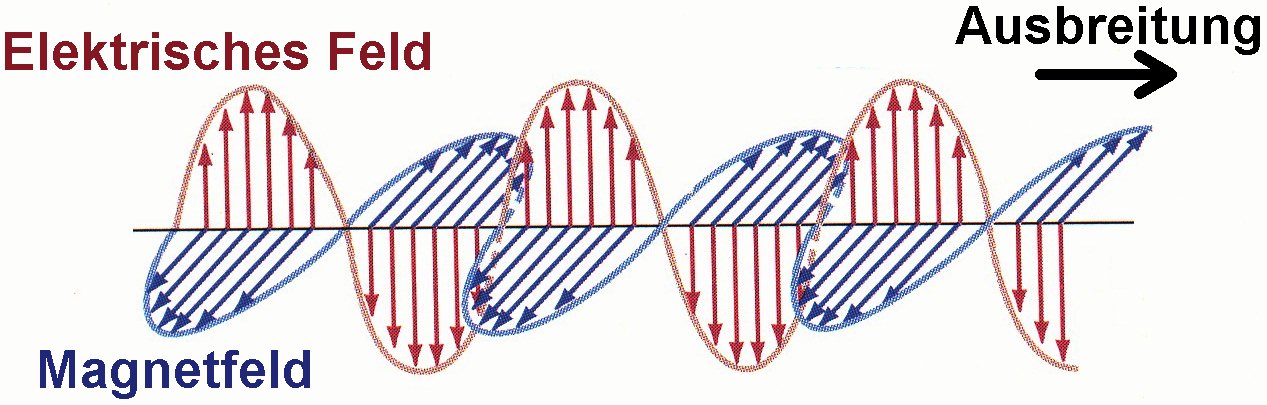
Genau eine solche elektromagnetische Welle wollen wir in diesem einfachen Experiment erzeugen und auch wieder detektieren. Dazu benötigen wir
- einen dickeren Draht bestehend aus einer einzelnen Litze
- einen Grillanzünder
- eine Neon-Glimmlampe
- Holz für die beiden Halterungen
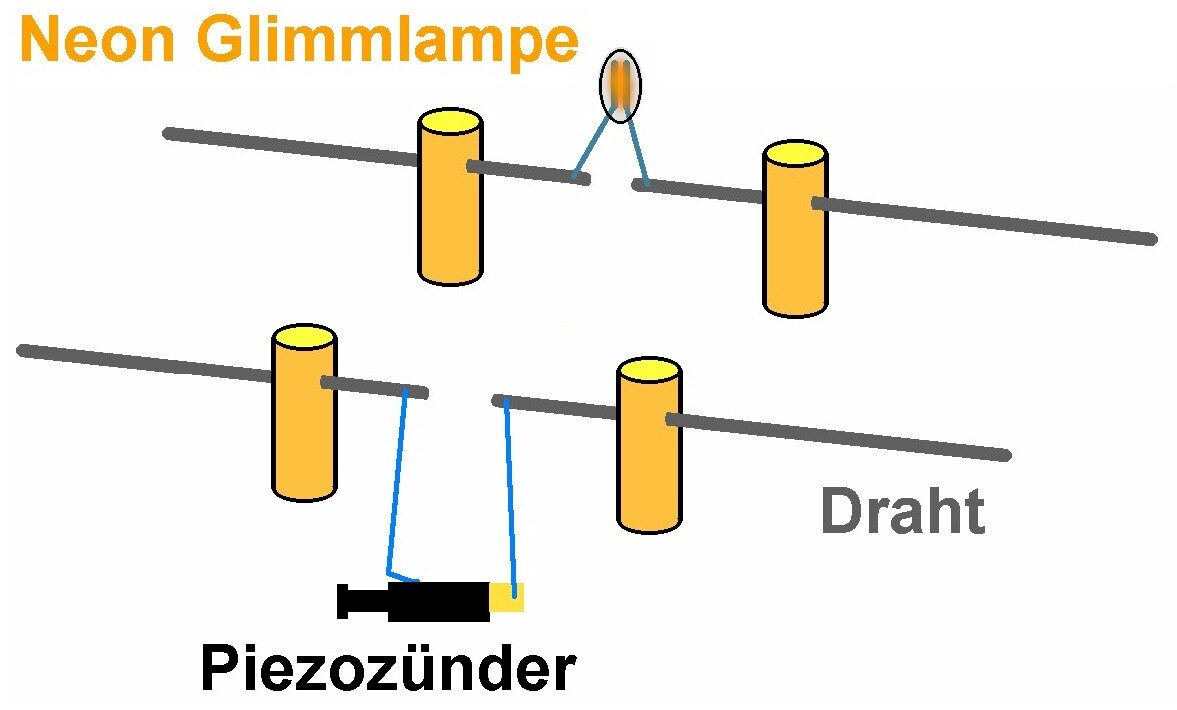
Den Grillanzünder habe ich um nur 1 Euro bei TEDI entdeckt:


Die Neon-Glimmlampen gibt es günstig auf ebay:


Als Draht für die Antenne nehme ich 2.5 mm² Aderleitung:

Den Piezozünder bauen wir aus dem Grillzünder aus:

Wir benötigen 4 Drahtstücke, wobei meine eine Länge von jeweils ca. 15–20 cm aufweisen:


Die Halterungen habe ich aus Holzresten gebastelt:

Meine Küche war zwischenzeitlich wieder einmal Werkstatt:

Der fertige Aufbau:


Befindet sich an der gekauften Glimmlampe noch ein Widerstand (für den Betrieb an 230V), so können wir diesen ohne Bedenken entfernen. Es reicht die reine Glimmlampe…

Die Drahtenden, an welche der Piezozünder angeschlossen ist, sollen einen Abstand von ca. 4-5 mm besitzen. Betätigt man nun den Piezozünder, bildet sich ein Funken zwischen den beiden Senderdrähten und die zwischen den beiden Empfängerdrähten befindliche Glimmlampe leuchtet kurz auf. Um dies zu sehen, dunkelt man am besten den Raum ein wenig ab.

Wir haben also auf einfachste Weise einen Sender und Empfänger für elektromagnetische Wellen gebaut, Heureka. Heinrich Hertz wäre stolz auf uns 😉
Schleuderschlauch
Für dieses Experiment wird nur ein geriffelter Installationsschlauch benötigt, welchen man in jedem Baumarkt bekommt.


Mit einem Bastelmesser längt man ihn auf eine Länge L ≈ 1 m ab. Danach nimmt man ein Ende in die Hand und schleudert den Schlauch mit zunehmender Geschwindigkeit in der Luft herum. Es sollten sich Töne mit steigender Frequenz/Tonhöhe ergeben…

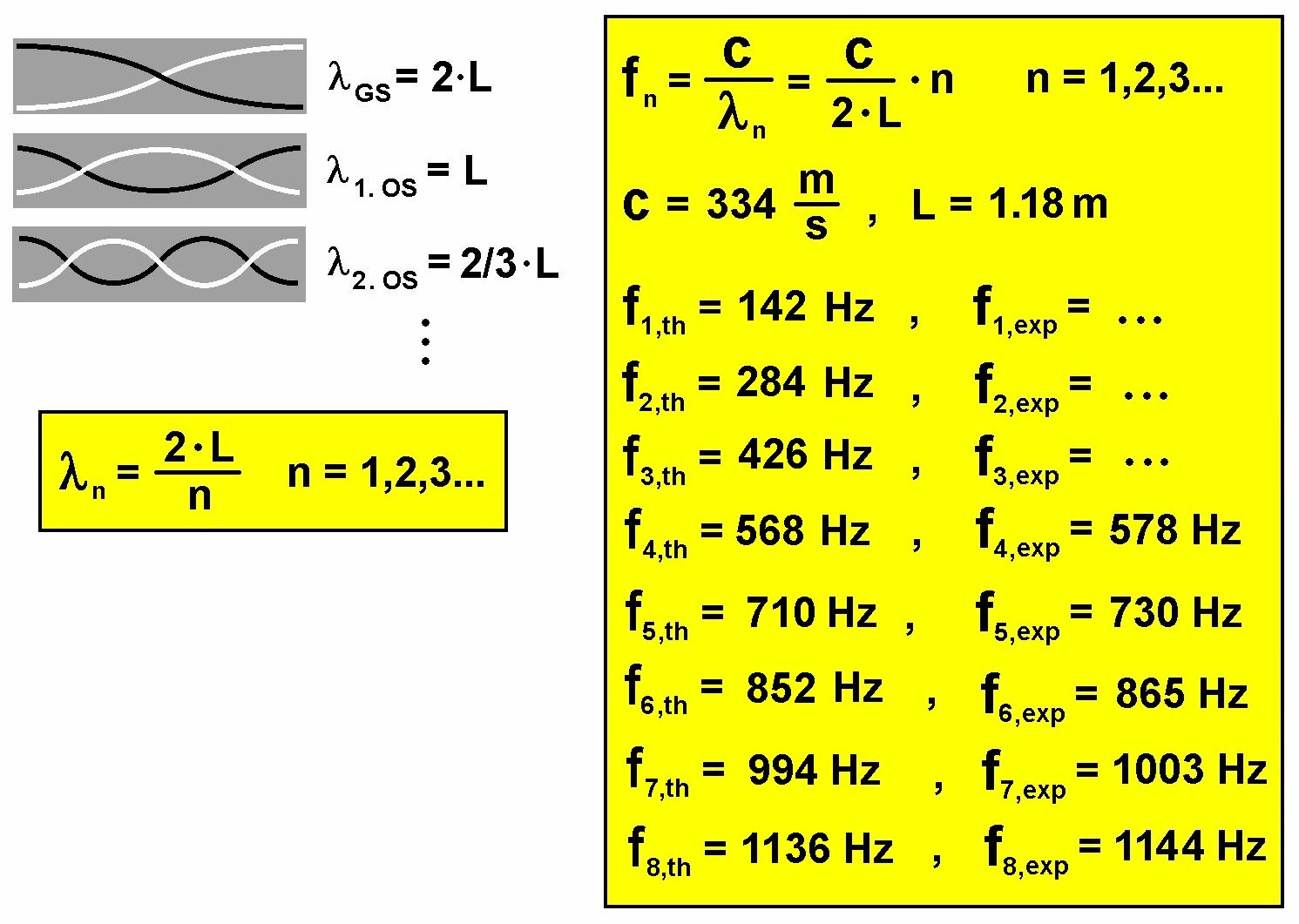
Wie entstehen diese Töne? Nun, am äußeren Ende des Schlauches strömt die Luft durch das Schleudern schnell vorbei und erzeugt dadurch (vgl. Bernoulligleichung) einen Unterdruck. Dieser bewirkt eine Luftströmung durch den Schlauch, wodurch Eigenschwingungen der Luft angeregt werden. Es handelt sich beim Schlauch um ein doppelseitig offenes Ende. Dadurch besitzen die Eigenschwingungen an ihren Enden einen Schwingungsbauch. Für die Grundschwingung gilt daher λ = 2 · L, für die erste Oberschwingung λ = 2 · L / 2, für die zweite Oberschwingung λ = 2 · L / 3 usw., also allgemein λ(n) = 2 · L / n mit n = 1, 2, 3, 4 …
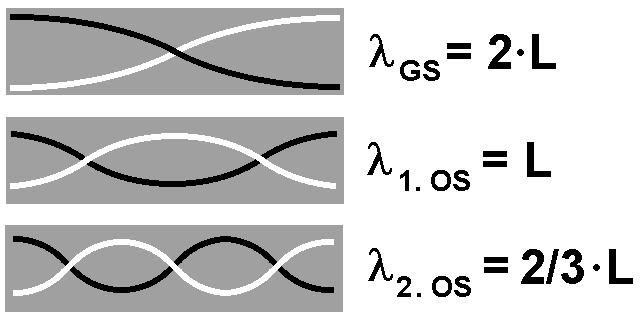
Für dieses Experiment benötigte ich wieder Hilfe von einem meiner Kinder. Zum Glück willigte Lorenz ein, mich zu unterstützen, vielen Dank dafür.

Die Qualität des Isolierrohrs ließ leider extrem zu wünschen übrig, es brach nämlich bereits nach kurzer Zeit immer ab. Zum Glück hatten wir 10 m zur Verfügung, welche wir auch fast zur Gänze benötigten. Man kann daher auch den nicht ganz ernst gemeinten Frust von Lorenz am Ende des Experiments verstehen 😉
Wer möchte, kann die erzeugten Töne mit einem Audiorecorder am Smartphone aufnehmen und dann mit einer Software, z.B. GRAM, analysieren.
Ich erhielt folgendes Frequenzspektrum:
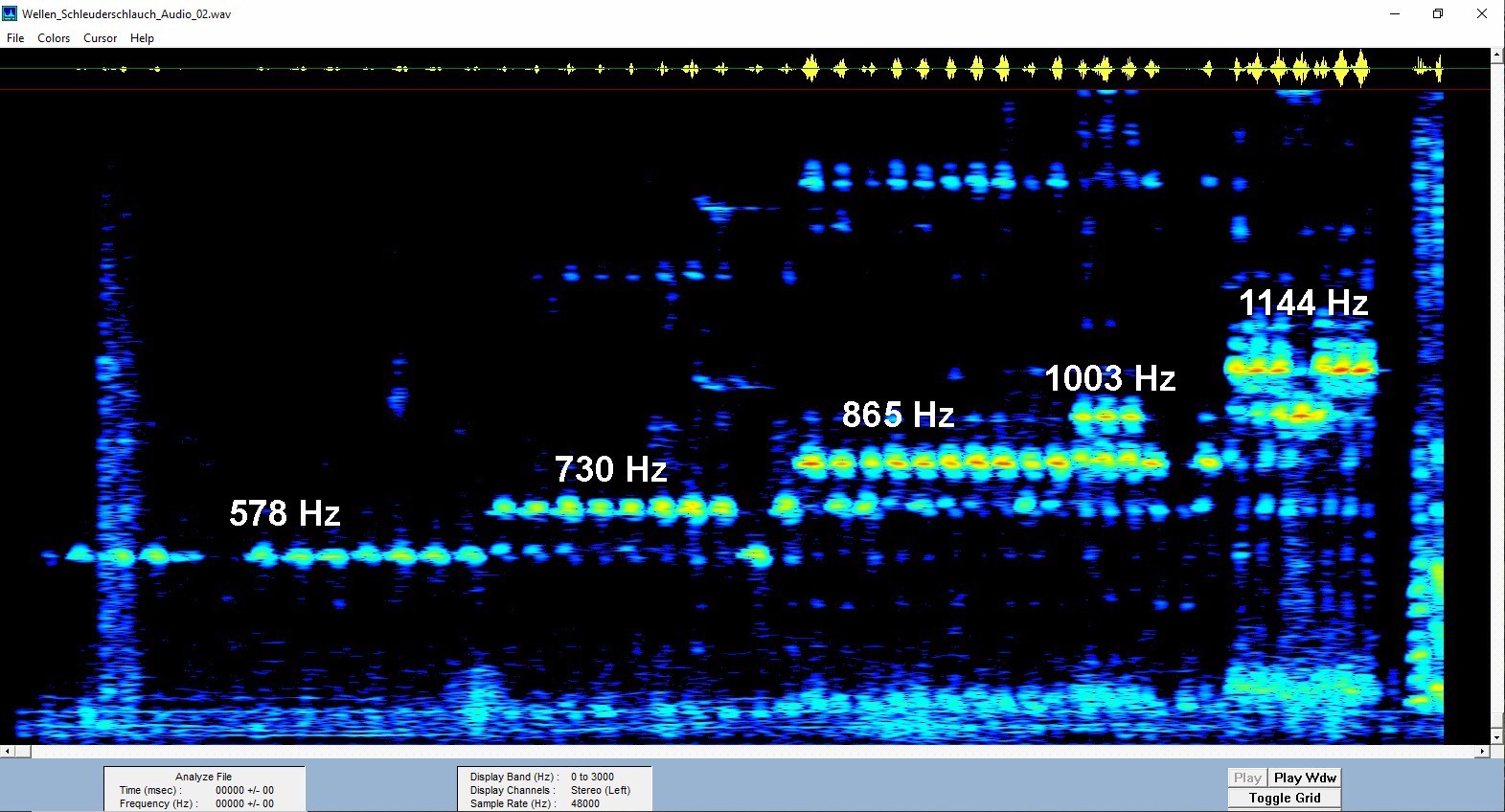
Die Länge des Schleuderschlauchs betrug 1.18 m. Demnach besitzt der Grundton eine Frequenz von 142 Hz. Diesen und die ersten beiden Obertöne mit f = 284 Hz bzw. 426 Hz konnte Lorenz nicht anregen. Dazu hätte der Schlauch noch viel langsamer geschleudert werden müssen. Für die weiteren Obertöne stimmte aber Theorie und Experiment relativ gut überein, Heureka…
Der Selbstbau-Kompass
Ein einfacher Kompass, welcher zuverlässig nach Norden zeigt, kann auch selbst gebastelt werden. Benötigt werden nur
- 1 mm Bohrer
- starker Magnet
- Korken
- doppelseitiges Klebeband
- Suppenteller
- Wasser





Zunächst magnetisiert man den 1 mm dünnen Bohrer mit einem starken Magneten, in meinem Fall ein Neodym-Würfelmagnet. Dazu streicht man mit dem Magnet unbedingt immer in der gleichen Richtung über den Bohrer! Das führt dazu, dass die Elementarmagnete im ferromagnetischen Bohrer gleich ausgerichtet werden und er selbst zum schwachen Magneten wird
Mit einem Bastelmesser schneidet man eine nicht zu dünne aber auch nicht zu dicke Scheibe vom Korken herunter…

und beklebt eine Seite mit dem doppelseitigen Klebeband. Auf dieses kommt dann der Bohrer:



Nun ist man fast fertig. Der Bohrerkompass muss nur noch in den mit Wasser gefüllten Suppenteller gelegt werden. Wie man es von einem Kompass erwartet orientiert er sich wie durch Zauberhand in Nord-Süd-Richtung:


Bei einem Kompass zeigt immer der magnetische Nordpol nach Norden. Demnach muss das Erdmagnetfeld im Norden einen magnetischen Südpol haben. Geografischer und magnetischer Pol sind allerdings nicht ident. Deshalb beträgt in Europa die Abweichung (sog. Missweisung) bis zu 20°. Die Orientierung des Erdmagnetfelds ändert sich zudem im Laufe der Zeit. Hier eine interessante Internetseite zu diesem Thema: https://worldoceanreview.com/de/wor-6/arktis-und-antarktis-naturraeume-in-poleposition/eine-kurze-geschichte-der-polarregionen/die-wandernden-pole-der-erde/
Der Cartesianische Taucher
Dieses einfache Experiment habe ich selbst als Schüler gebastelt. Ich kann mich noch gut daran erinnern, wie stolz ich damals war, als es funktionierte 😉
Benötigte Teile:
- Den Stöpsel eines Kugelschreibers
- Büroklammern
- ein Feuerzeug
- eine verschließbare Plastikflasche
- Wasser
- ggf. eine Zange





Vom Kugelschreiber benötigt man nur den Stöpsel. Dieser darf am oberen Ende allerdings kein Loch besitzen, dafür aber eine dünne Verlängerung an der Unterseite…

Mit dem Feuerzeug erhitzt man nun das eine Ende einer Büroklammer und steckt es dann durch die Verlängerung des Kugelschreiberstöpsels:

Legt man nun den Stöpsel in ein großes mit Wasser gefülltes Gefäß, so wird er zunächst noch sehr weit aus der Wasseroberfläche herausragen.

Daher müssen wir ihn nun mit weiteren Büroklammern beschweren und zwar solange, bis nur noch ganz wenig aus dem Wasser herausragt. In meinem Fall waren dazu insgesamt 4 Büroklammern nötig:

Jetzt gibt man den Cartesianischen Taucher in die fast zur Gänze mit Wasser gefüllte Flasche und verschließt diese gut. Zunächst wird der Taucher noch oben an der Wasseroberfläche schwimmen:

Drückt man nun aber die Flasche kräftig zusammen, so sinkt der Taucher:

Lässt man die Hand wieder locker, so steigt der Taucher wieder auf. Warum ist dies der Fall? Der Auftrieb in einer Flüssigkeit ist gleich dem Gewicht der verdrängten Flüssigkeit. Zunächst noch ohne Handdruck ist die Luftblase im Inneren des Tauchers groß und verdrängt dadurch viel Wasser. Die Auftriebskraft ist demnach ebenfall hoch und der Taucher schwimmt oben an der Oberfläche. Presst man nun die Flasche zusammen, erhöht sich der Druck im Inneren der Flasche. Wasser kann als Flüssigkeit aber nahezu nicht komprimiert werden, die Luftblase im Inneren des Stöpsels aber sehr wohl. Ist sie kleiner, verdrängt sie auch weniger Wasser und der Auftrieb nimmt ab. Dadurch sinkt der Cartesianische Taucher zu Boden.
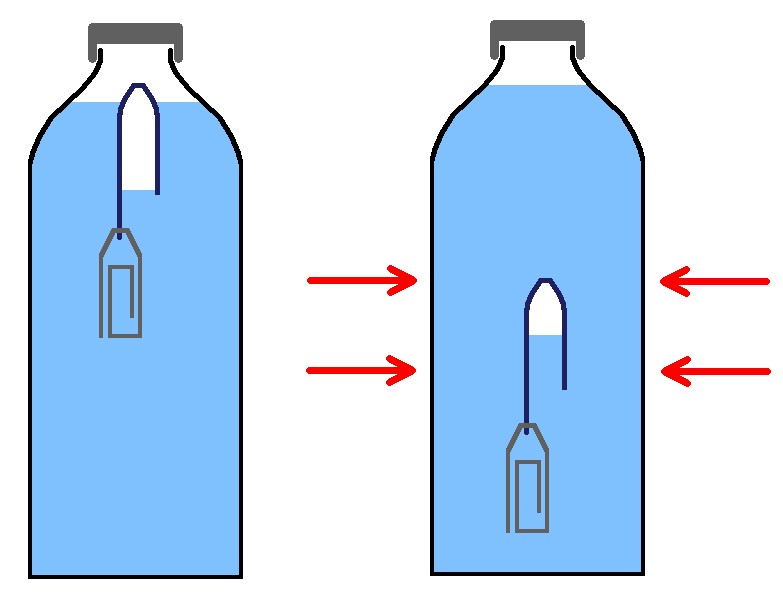
Die kippende Stange
Dieses Experiment behandelt eindrücklich die physikalischen Größen Drehmoment T und Trägheitsmoment I. Man benötigt nur folgende Dinge dafür:
- Legoteile oder einen Holzspieß
- eine schwere Kugel, welche man auf den Holzspieß aufschieben kann oder wie in meinem Fall zwei Bleikugeln
- Klebeband zum Fixieren des Spießes am Boden
- Smartphone oder Stoppuhr
- Software Tracker
Es geht um folgende Frage:
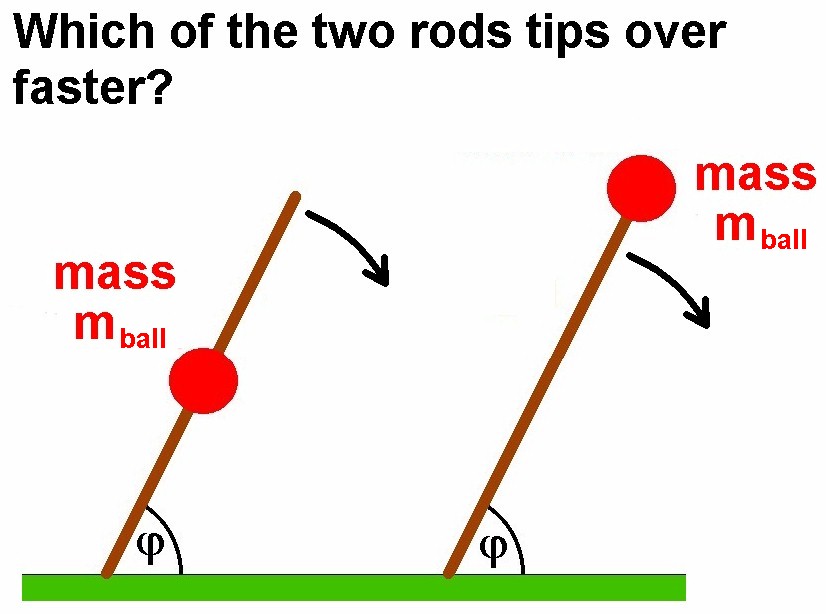
Man postiert also die schwere Kugel einmal in der Mitte der Stange und dann am Stangenende und lässt diese vom gleichen Startwinkel aus kippen. Welche der beiden Stangen kippt schneller?
Die berühmte Newtonsche Bewegungsgleichung lautet ja F = m · a. Für die Rotation tritt das Drehmoment T an die Stelle der Kraft F, statt der Masse m spielt nun das Trägheitsmoment I eine Rolle und die Beschleunigung a wird durch die Winkelbeschleunigung α ersetzt. Wir erhalten also die Bewegungsgleichung der Rotation: T = I · α.
Es gilt weiters:
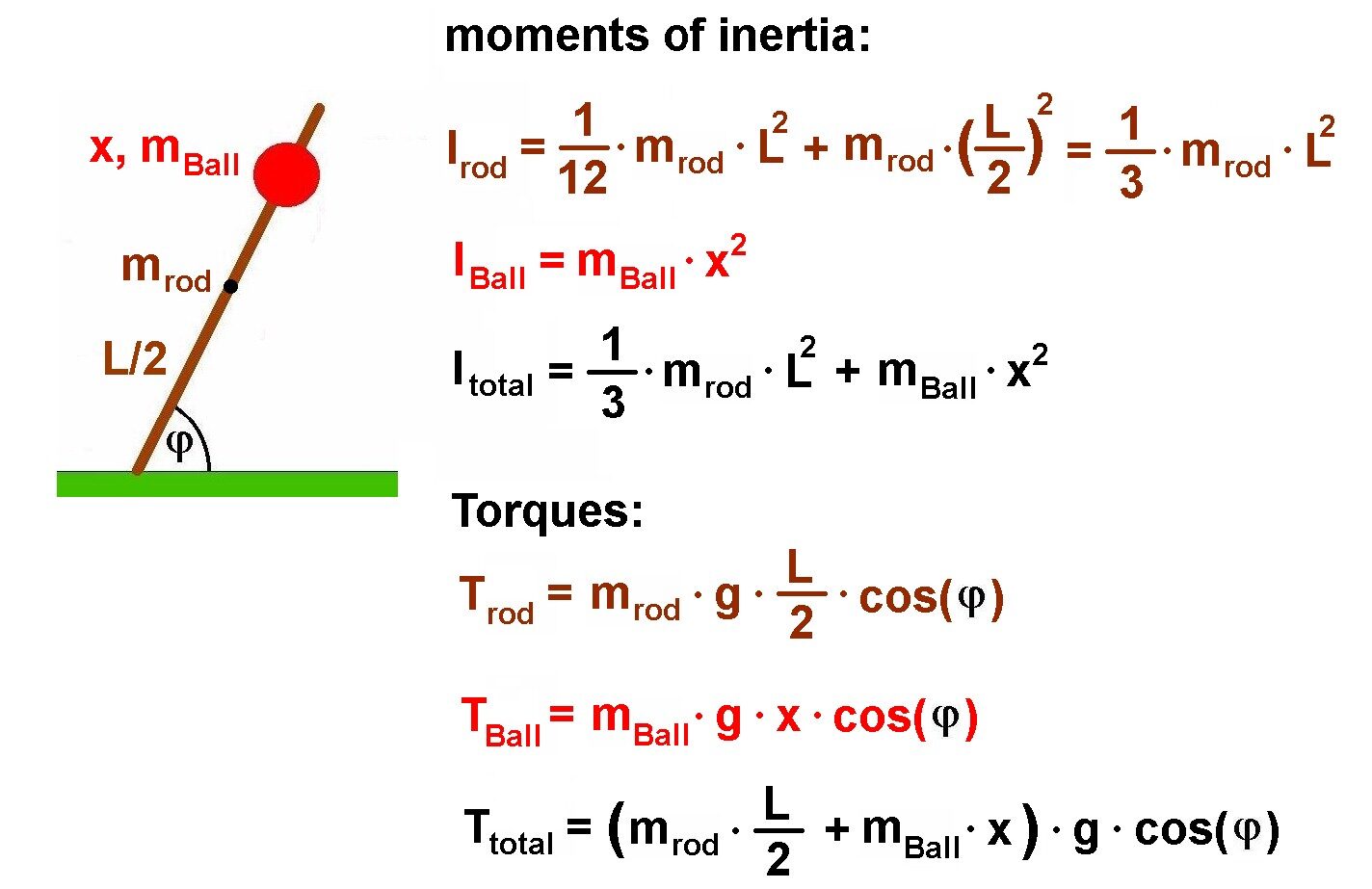
Versuchen wir zunächst dieses Experiment mittels EXCEL zu simulieren. Wir kennen also das wirkende Drehmoment T in Abhängigkeit vom Winkel φ und das Trägheitsmoment der gesamten Stange inklusive Ball. Also können wir mittels T = I · α die momentane Winkelbeschleunigung α bestimmen. Die Winkelbeschleunigung α ist aber die zeitliche Ableitung der Winkelgeschwindigkeit ω, es gilt daher α = dω/dt ≈ Δω/Δt. Kennen wir α und die Zeitschrittweite Δt, so kennen wir auch die Änderung der Winkelgeschwindigkeit Δω. Ist weiters die Winkelgeschwindigkeit zu Beginn des Zeitintervalls Δt bekannt, so lässt sich über Δω die Winkelgeschwindigkeit am Ende des Zeitintervalls Δt berechnen. Die Winkelgeschwindigkeit ist aber weiters die zeitliche Ableitung des Winkels, also ω = dφ/dt ≈ Δφ/Δt. Jetzt geht man gleich vor wie bei der Winkelbeschleunigung. Kennt man Δt, so kann man bei bekannter Winkelgeschwindigkeit die Änderung des Winkels Δφ ermitteln. Kennt man den Winkel am Beginn des Zeitintervalls Δt, so weiß man daher auch den Winkel am Ende des Zeitintervalls Δt. Man verwendet hier aber um eine höhere Genauigkeit der Simulation zu erzielen nicht die Winkelgeschwindigkeit am Beginn oder am Ende des Zeitintervalls, sondern den Mittelwert der beiden. Zum Schluss verwendet man den neuen Winkel φ wieder zur Berechnung des Drehmoments T und die obigen Schritte wiederholen sich.
Hier noch einmal die Berechnungsroutine:
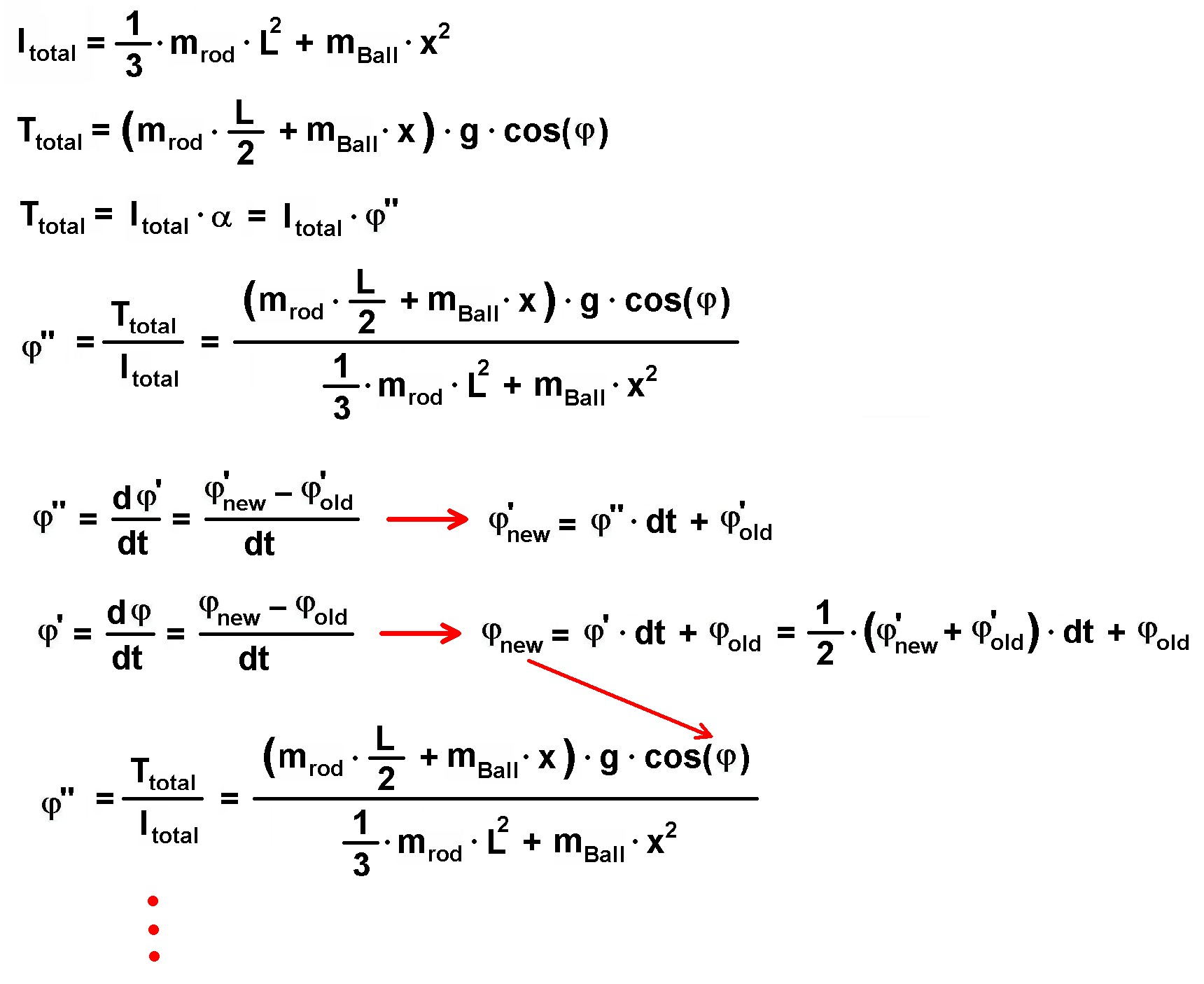
EXCEL nimmt einem diese Vielzahl an Berechnungen wunderbar ab. Das fertige „Programm“ sieht dann wiefolgt aus:
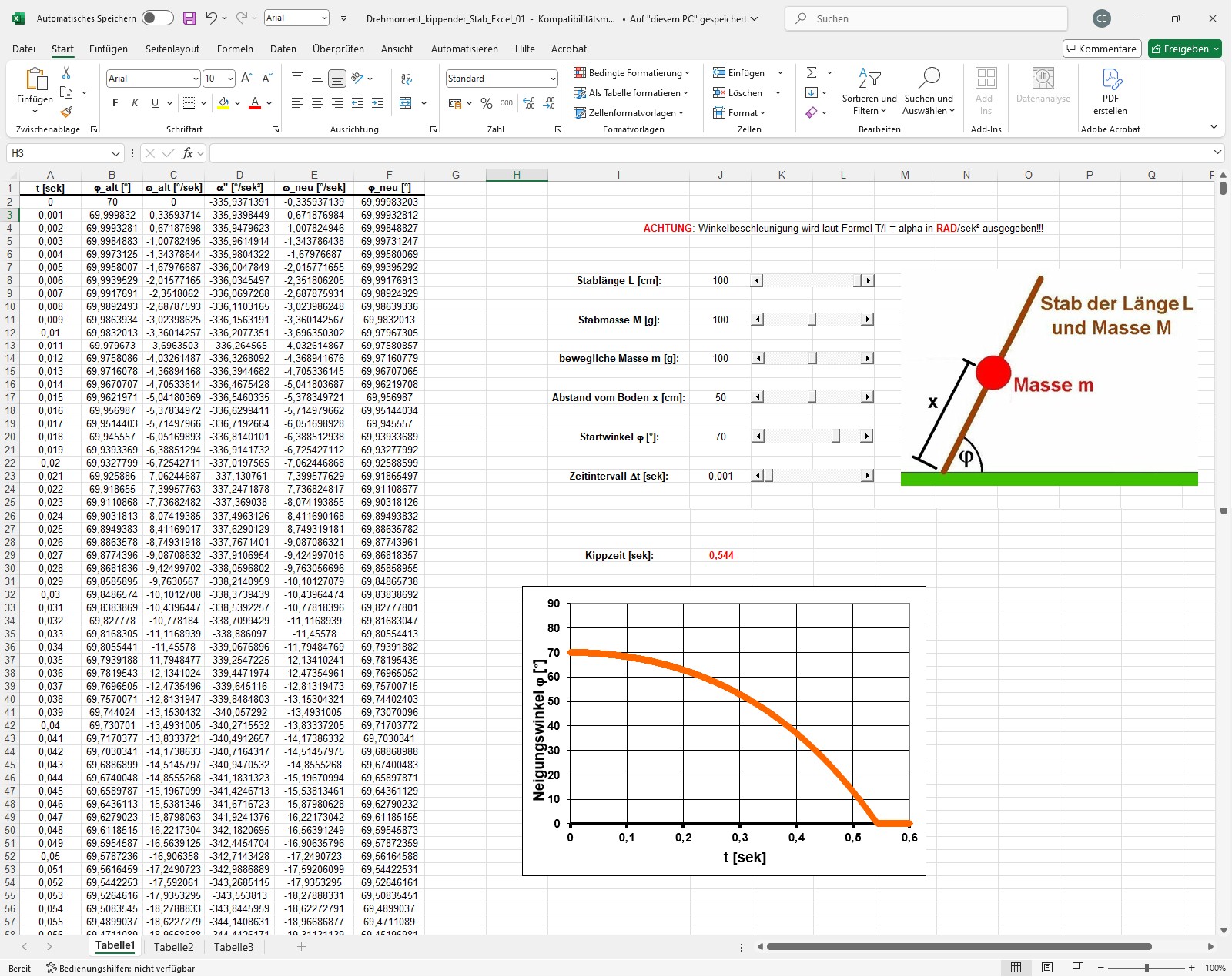
Ein typischer Graph φ(t) sieht dann zum Beispiel so aus:
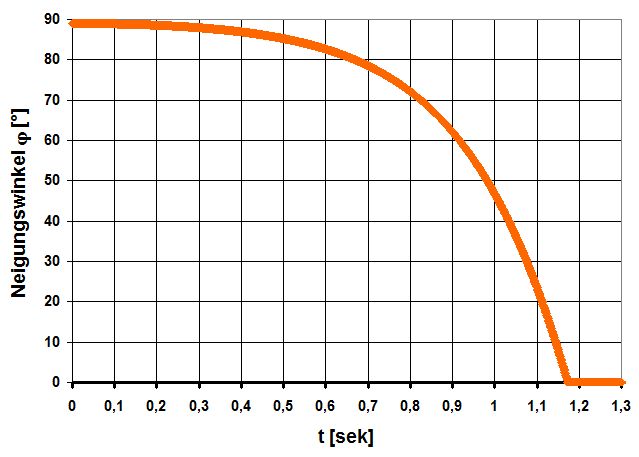
Der Startwinkel dieser konkreten Simulation betrug 89°, zu Beginn steht der Stab also nahezu senkrecht. Dadurch ist das wirkende Drehmoment T anfangs sehr gering und der Winkel φ wird nur sehr langsam kleiner. Mit zunehmenden Winkel erhöht sich aber das Drehmoment und die Winkelbeschleunigung α und damit auch die Änderung der Winkelgeschwindigkeit bzw. des Winkels nehmen zu. Nach ca. 1.17 sek berührt der Stab den Boden.
EXCEL-Datei: Drehmoment_kippender_Stab_Excel_01
Nun zum Experiment:



Die Masse der beiden Bleikugeln beträgt inkl. Achse 73 g:

Den kippenden Stab habe ich aus LEGO-Teilen gebastelt:




Dessen Masse beträgt 21 g:

Die Stablänge beträgt 33.5 cm, die Bleikugeln befinden sich bei x = 32 cm am Ende des Stabs bzw. bei x = 16 cm in dessen Mitte:



Zuerst Kugel am Stabende:

Man stoppt entweder die Kippzeit oder man nimmt ein Video auf und analysiert den Kippvorgang mit der Software Tracker:
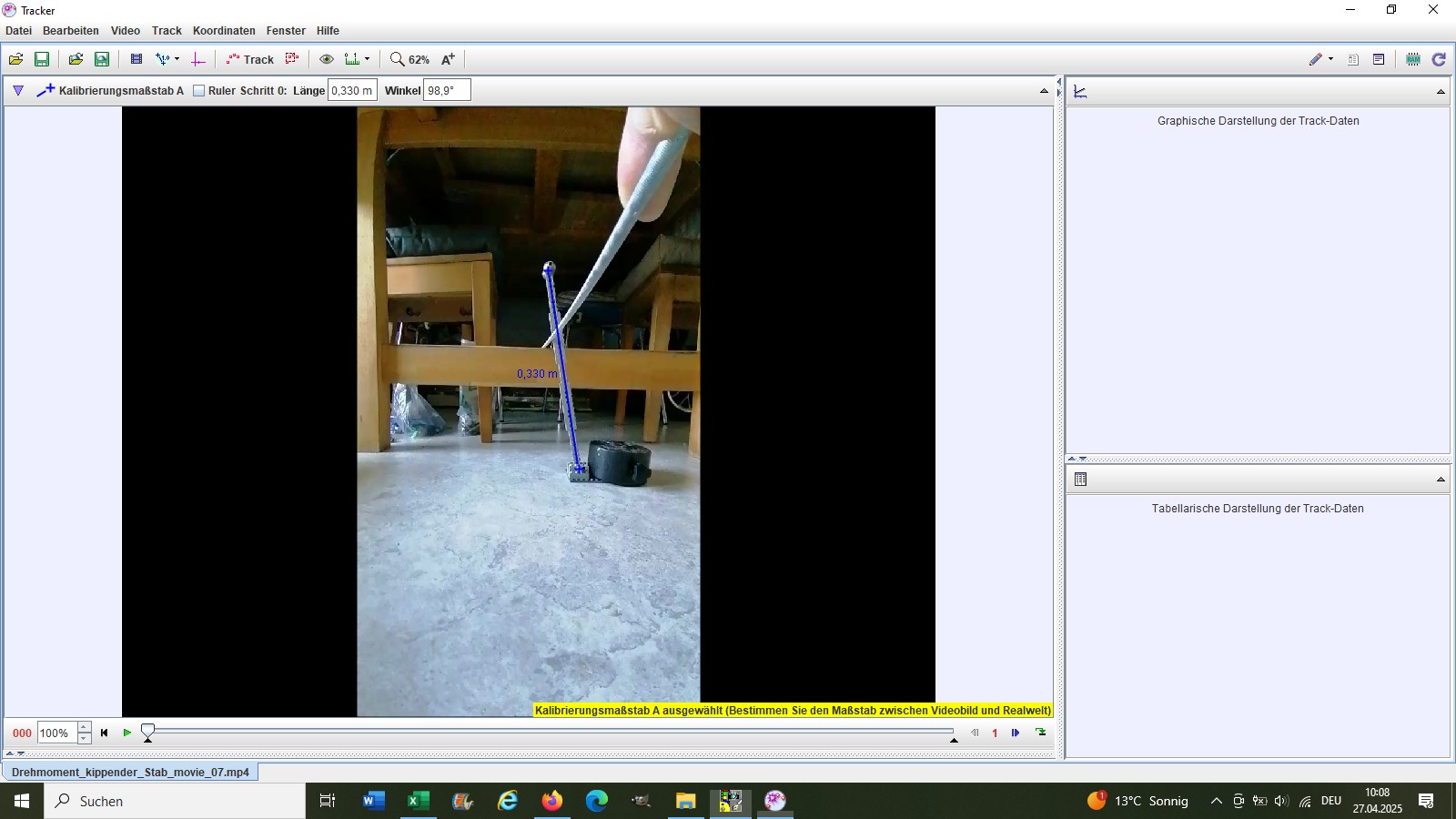
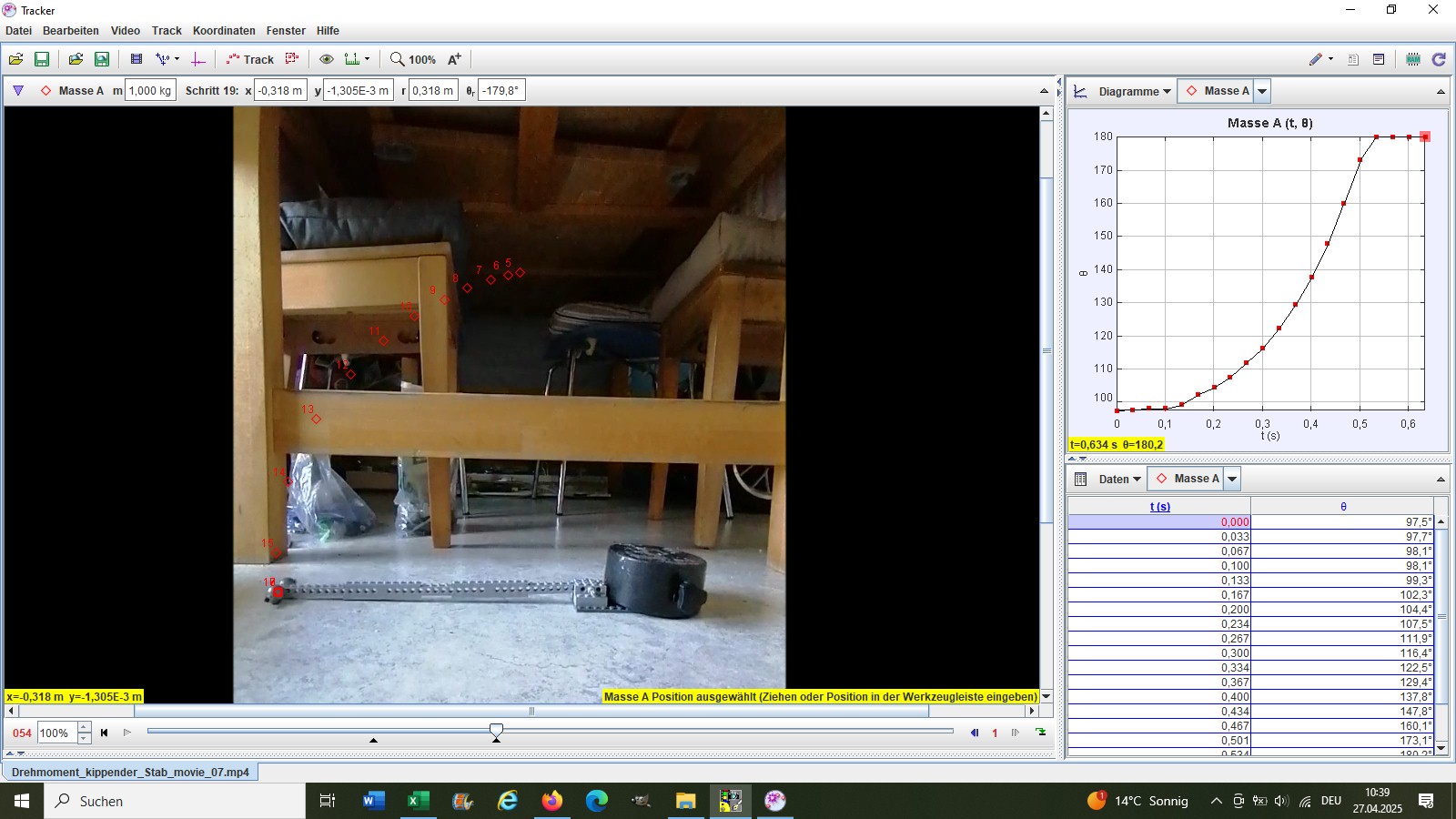
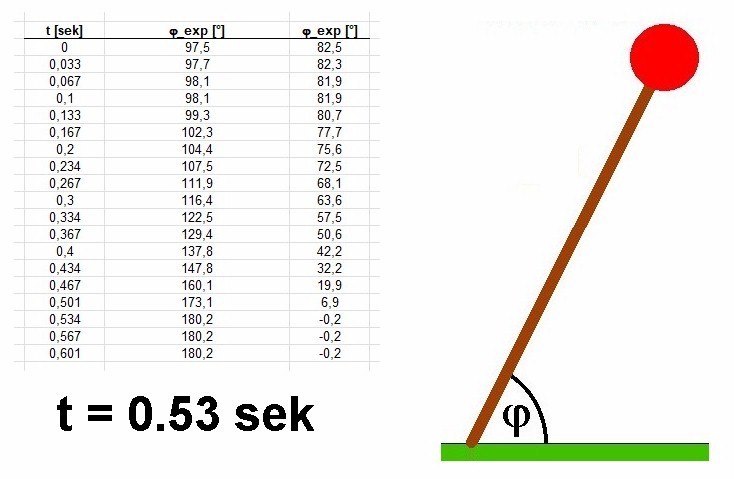
Die Kippzeit beträgt in diesem Fall also rund 0.53 Sekunden. Hier die Gegenüberstellung von Experiment und Theorie:
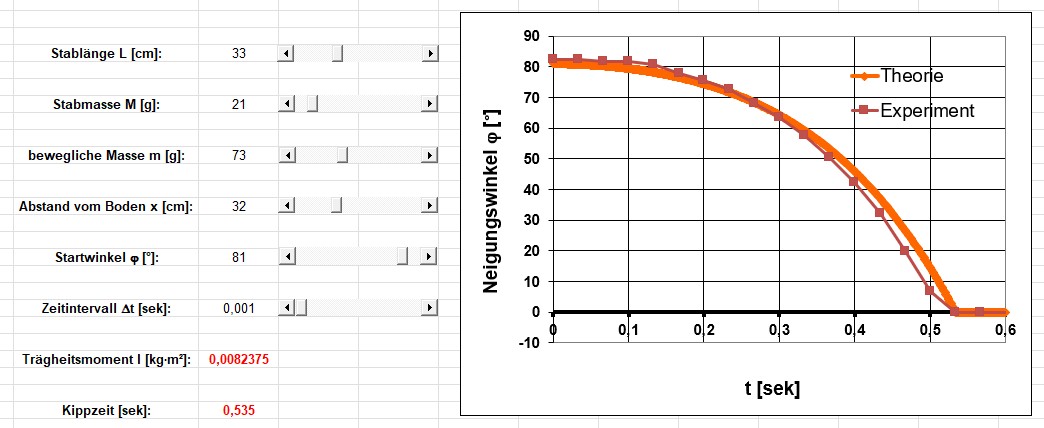
Jetzt Kugel in der Stabmitte:

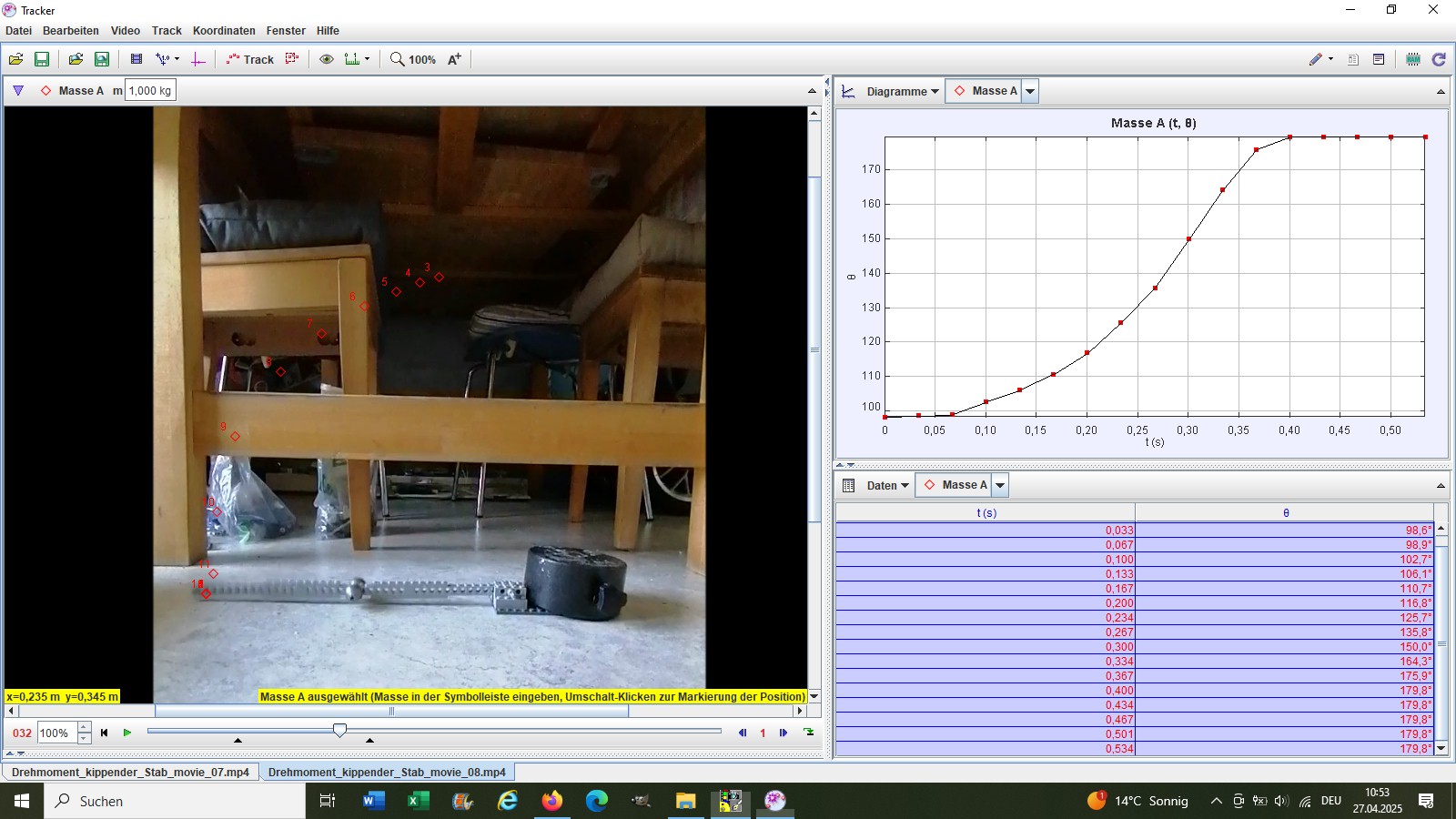
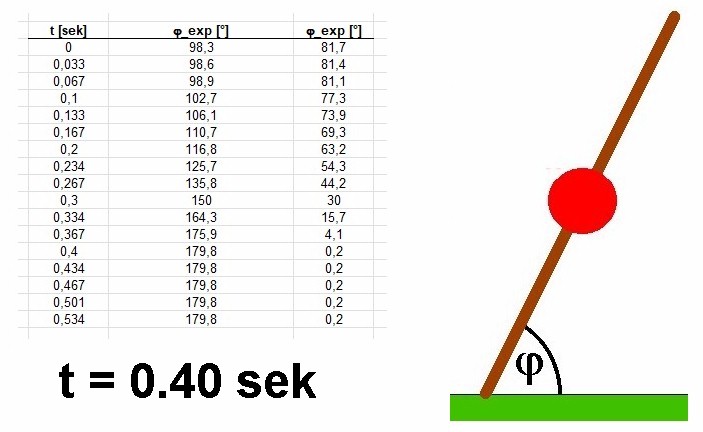

Mit der Kugel in der Stabmitte beträgt die Kippzeit nun nur noch 0.4 sek, die Stange kippt in diesem Fall also schneller. Warum ist dies so?
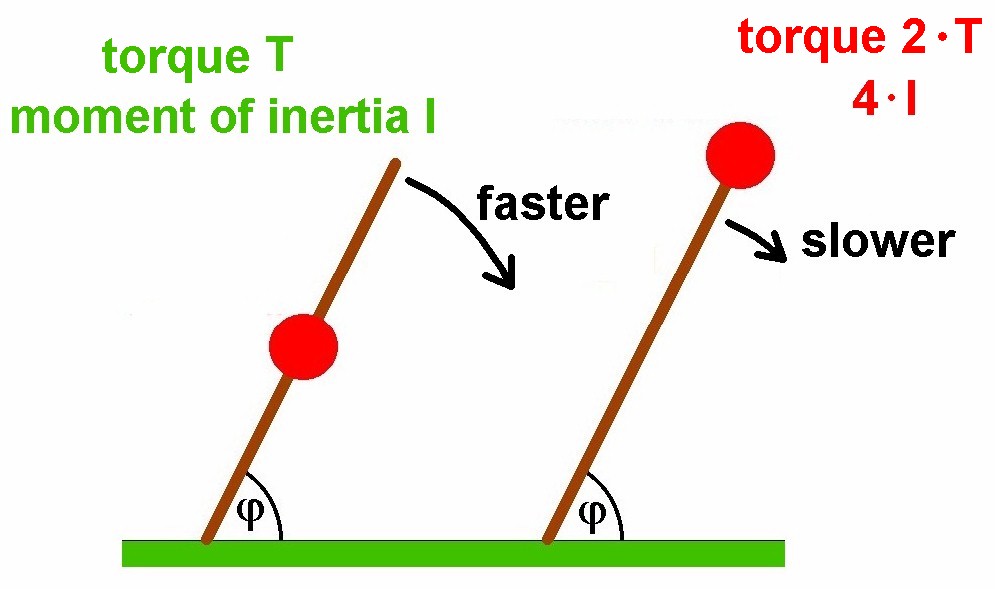
Nun vernachlässigen wir einmal das Trägheitsmoment I der Stange. Befindet sich die Kugel in der Stabmitte, so wirkt das Drehmoment T und das Trägheitsmoment I. Mit der Kugel am Stabende steigt nun das Drehmoment aufgrund des doppelt so großen Hebels auf 2 · T, das Trägheitsmoment wächst allerdings auf den 4-fachen Wert (Anm.: I = m · r²). Daher ist die Winkelbeschleunigung α = T / I im zweiten Fall geringer und der Stab mit der Kugel am Ende kippt langsamer, Heureka …
Helmholtz-Resonator

Bildquelle: https://de.wikipedia.org/wiki/Helmholtz-Resonator#/media/Datei:Helmholtz_resonator.jpg, CC BY-SA 2.5
Ein Helmholtz-Resonator (benannt nach Hermann von Helmholtz, 1821 – 1894) ist ein akustischer Resonator. Helmholtz entwickelte diesen Resonator im Jahre 1859, um mit seinem Ohr an der oberen spitzen Öffnung einen einzigen Grundton aus einem Klanggemisch nachzuweisen, das in die untere Öffnung eindringt. Der Resonator wurde anfangs aus Glas geblasen und später aus Messingblech geformt. Ein alltägliches Beispiel für einen Helmholtz-Resonator ist eine Flasche, die am Hals angeblasen einen Ton erzeugt. Genau dem wollen wir uns nun widmen.


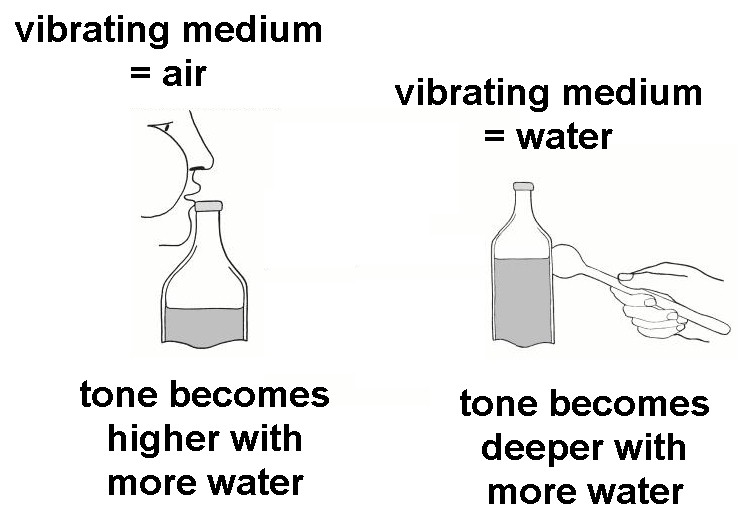
Wir benötigen also für diesen Versuch lediglich eine Glasflasche mit schmalen Hals und Wasser, welches wir dann in die Flasche füllen, um das Luftvolumen V ändern zu können. Mit dem Mund blasen wir dann oben über die Flaschenöffnung und bestimmen mit einer Smartphone-App die Frequenz f des erzeugten Tons.

Quelle: Universität Augsburg, Institut für Didaktik der Physik, CD-ROM Freihandexperimente
Für die Frequenz f gilt dann folgende Formel:
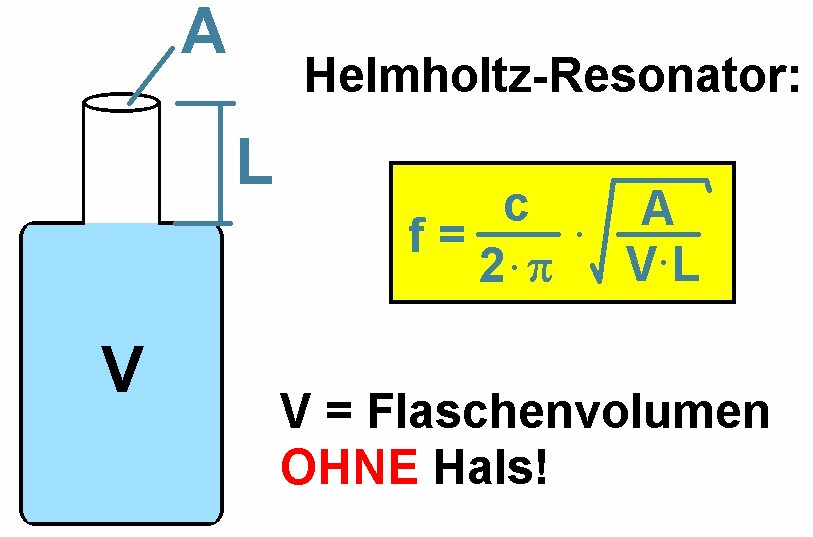
Ich habe auch ChatGPT befragt und dieser lieferte mir noch einen Korrekturfaktor für die Halslänge L:

Zuerst müssen verschiedene Volumina bestimmt werden. Dazu habe ich die leere Flasche auf die Waage gestellt und den Tara-Knopf gedrückt:


Danach füllte ich Wasser bis zu jener Stelle in die Flasche, wo der Flaschenhals beginnt. Bei mir waren dazu 700 ml = 700 g notwendig:



Dies war meine 0-Markierung. Sodann schüttete ich immer genau 100 g Wasser aus und markierte den Wasserspiegel mit 100 ml, 200 ml, 300 ml usw.:

Ganz ohne Wasser betrug das Luftvolumen V bis zum Hals wie schon erwähnt genau 700 ml. Jetzt füllte ich wieder Wasser bis zu den jeweiligen Markierungen ein, bließ mit dem Mund über die Flaschenöffnung und bestimmte mit einer Frequenzspektrum-App die Tonfrequenz f:

Diese experimentell ermittelte Frequenz stellte ich dann der Theorie gegenüber. Für die Formel benötigte ich noch die Länge L = 10.5 cm des Flaschenhalses und den Radius r = 1.0 cm der Flaschenöffnung:


Die beiden Graphen stimmen für größere Volumina sehr gut überein, Heureka…

Mit zunehmenden Wasserstand nimmt also die Frequenz bzw. Tonhöhe zu. Wenn man allerdings mit einer Gabel gegen die Flasche schlägt, so nimmt die Tonhöhe des auf diese Weise erzeugten Tons mit zunehmenden Wasserstand ab. Dies deshalb, weil beim Blasen über der Flaschenöffnung die Luft zum Schwingen gebracht wird, beim Schlagen mit der Gabel ist es aber das Wasser!
Quelle: Universität Augsburg, Institut für Didaktik der Physik, CD-ROM Freihandexperimente
Farbchromatographie
Mittels dieser einfachen Methode mit Haushaltsartikeln können die einzelnen Bestandteile von verschiedenen Filzstiftfarben aufgeschlüsselt werden. Damit kommen die Schülerinnen erstmalig selbst in Kontakt mit dem wichtigen Thema Chromatographie.
Man benötigt nur weißen Kaffeefilter, verschiedenfärbige Filzstifte, ein Glasgefäß und Wasser. Der komplette Versuch im Überblick:

Da ich keine weißen Kaffeefilter zuhause hatte, besorgte ich mir weißes Filterpapier und Filzstifte auf Amazon:






Auf einen der kreisrunden Filter zeichnet man mit den Filzstiften kurze Kreisbögen:

Mit dem zweiten Filter formt man ein Röhrchen und steckt dieses in die Mitte des bemalenen Filters:

Danach füllt man ein Glasgefäß fast vollständig mit Wasser und legt die beiden Filter oben aufs Glas. Das Filterröhrchen muss natürlich möglichst weit ins Wasser eintauchen:


Jetzt muss man eigentlich nur noch warten und beobachten. Das durchs Filterrohr angesaugte Wasser breitet sich im bemalenen Filter von innen nach außen aus und nimmt dabei die einzelnen Farbkomponenten unterschiedlich stark mit. Dadurch spalten sich die färbigen Kreisbögen in ihre Farbkomponenten auf. So besteht etwa die Farbe Schwarz nicht aus einer „schwarzen“ Komponente, sondern aus mehreren. Aber auch andere Filzstiftfarben zeigen spannende Farbaufspaltungen 😉

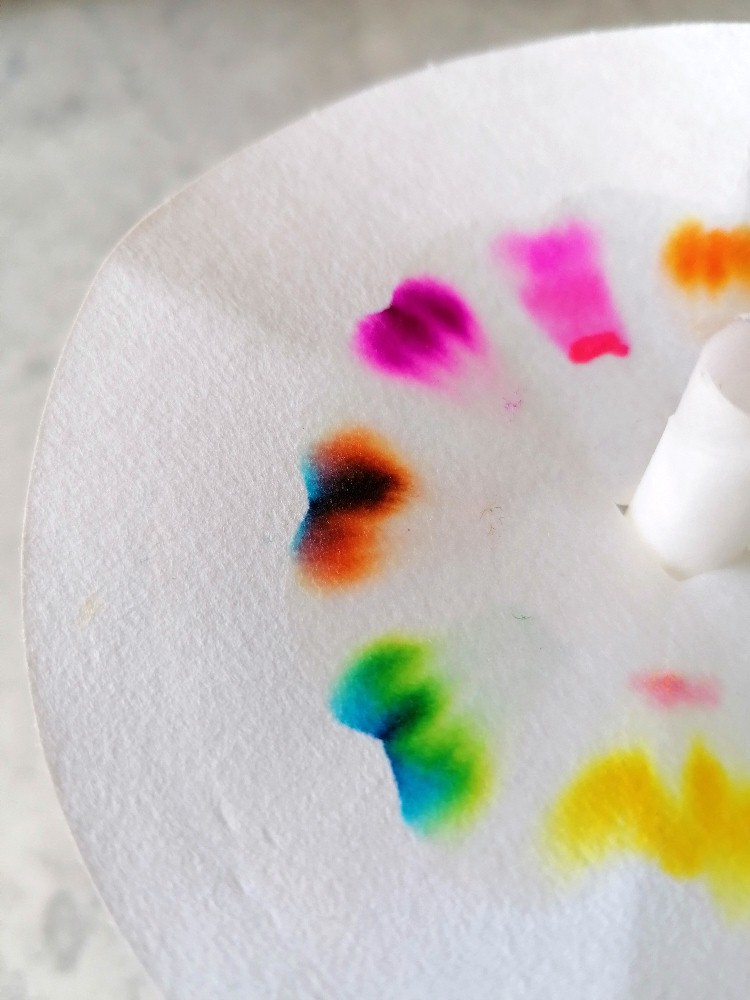



Diamagnetisches Wasser
Nähert man eine ferromagnetische Schraube einem Magneten, so wird diese angezogen. Der Grund liegt darin, dass sich in der Schraube zum Magneten zugewandt ein entgegengesetzter Magnetpol ausbildet. Weist etwa der Nordpol des Magneten zur Schraube, so bildet sich an der zum Magneten zugewandten Seite ein Südpol in der Schraube aus und die Schraube, aber auch der Magnet ziehen sich infolgedessen gegenseitig an:
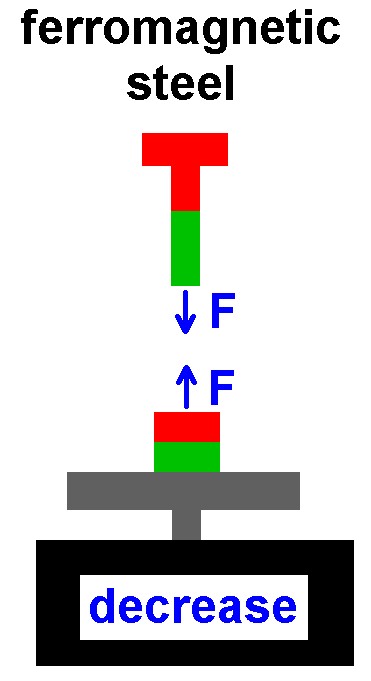
Befindet sich der Magnet auf einer Feinwaage, so zeigt diese bei Annäherung der Schraube weniger an!



Man sieht sehr schön die Abnahme der angezeigten Masse:

Was passiert aber, wenn man nun Wasser dem Magneten auf der Waage nähert? Was vermutlich nicht viele wissen, Wasser ist diamagnetisch und verhält sich daher anders als man es von den ferromagnetischen Stoffen gewohnt ist. Weist etwa der Nordpol des Magneten nach oben, so bildet sich im Wasser auf der dem Magneten zugewandten Seite nun atypisch auch ein Nordpol:

Infolgedessen wird das Wasser nach oben gedrückt und der Magnet auf der Waage nach unten. Die Anzeige auf der Waage müsste also steigen…

Und in der Tat ist eine sehr geringe Massenzunahme feststellbar:
Diamagnetische Effekte sind aber viel, viel schwächer als die bekannten ferromagnetischen. Von daher beträgt die Massenzunahme durch das angenäherte Wasser konkret nur 9 mg. Aber man konnte es eindeutig beobachten, Heureka…
Münzkatapult
Mit diesem sehr einfachen Versuch lassen sich die Größen potentielle und kinetische Energie bzw. der Energieerhaltungssatz sehr schön veranschaulichen. Benötigt wird nur eine längere Holzleiste, zwei Münzen und ein kurzes Rohrstück.

Die beiden Münzen werden im Abstand L bzw. 2 · L zur Drehachse/Plastikrohr auf der Leiste postiert:




Danach schlägt man mit der Hand fest auf das freie Ende der Holzleiste:

Die beiden Münzen werden daraufhin in die Luft geschleudert. Doch wie hoch kommen die beiden Münzen? Die Holzleiste dreht sich mit einer gewissen Winkelgeschwindigkeit ω. Für die Bahngeschwindigkeit gilt v = ω · r. Da sich die zweite Münze doppelt so weit von der Drehachse befindet wie die erste, ist deren Abschussgeschwindigkeit v durch das doppelte r auch doppelt so groß. Es gilt also v2 = 2 · v1! Für die kinetische Energie eines Körpers gilt ja die Formel Ekin = 1/2 · m · v². Eine doppelt so große Geschwindigkeit bedeutet durch das Quadrat die 4-fache kinetische Energie!

In der Luft tauschen sich ohne Reibung kinetische und potentielle Energie aus. Am höchsten Punkt besitzt die Münze keinerlei kinetische Energie, dafür maximale potentielle Energie Epot = m · g · h. Die kinetische Startenergie ist dann vollständig in die maximale potentielle Energie geflossen. Durch die 4-fache kinetische Startenergie der äußeren Münze besitzt diese am Umkehrpunkt auch die 4-fache potentielle Energie. Die äußere Münze muss also 4-mal so hoch geschleudert werden…

Das aufgenommene Video:
Mit der Software Tracker lässt sich dieses dann sehr einfach analysieren.

Die innere Münze besitzt laut Analyse eine Startgeschwindigkeit v1 = 1.44 m/s und eine maximale Flughöhe h1 = 0.154 m:
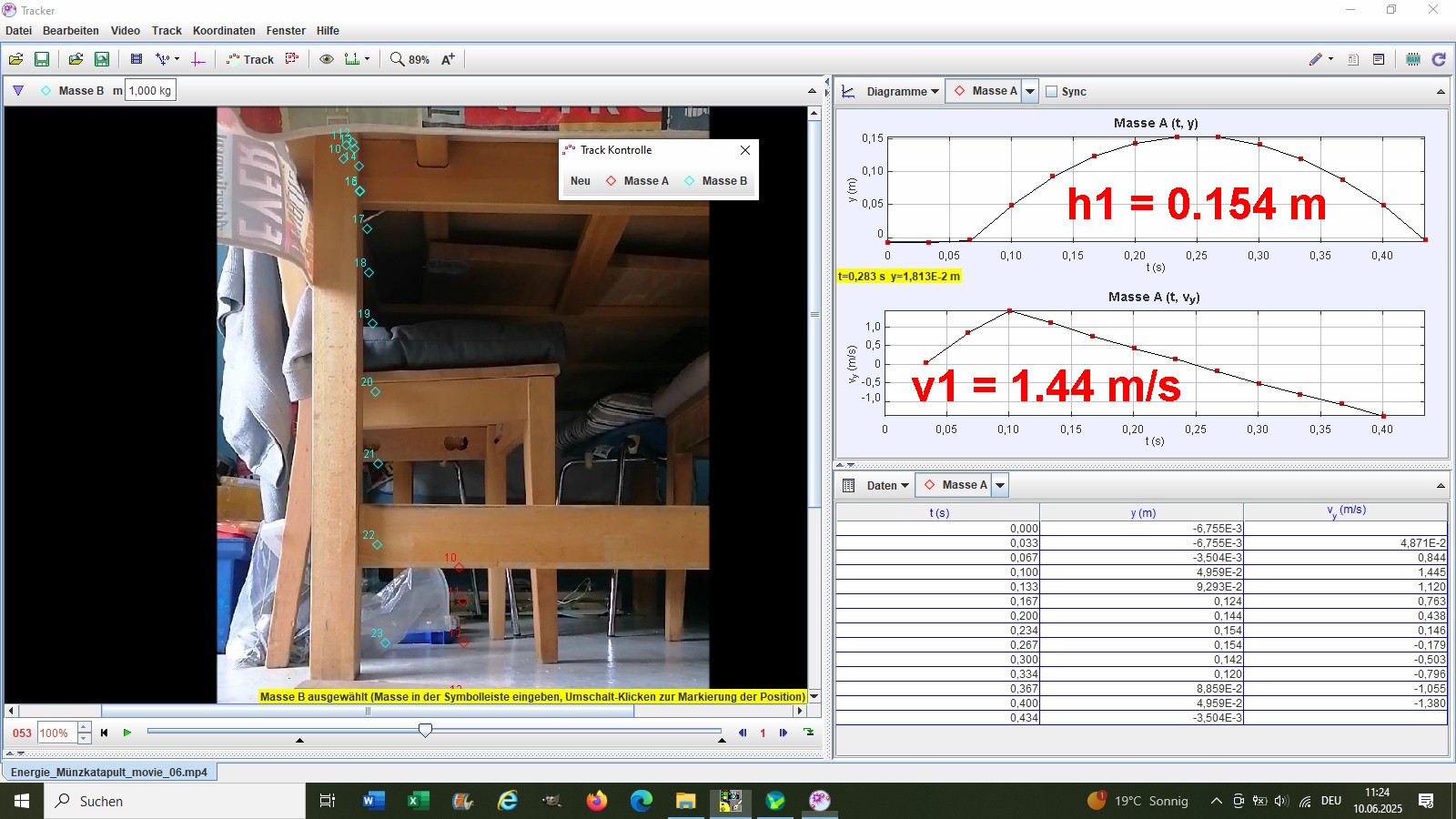
Für die äußere Münze gilt v2 = 2.96 m/s und h2 = 0.516 m:
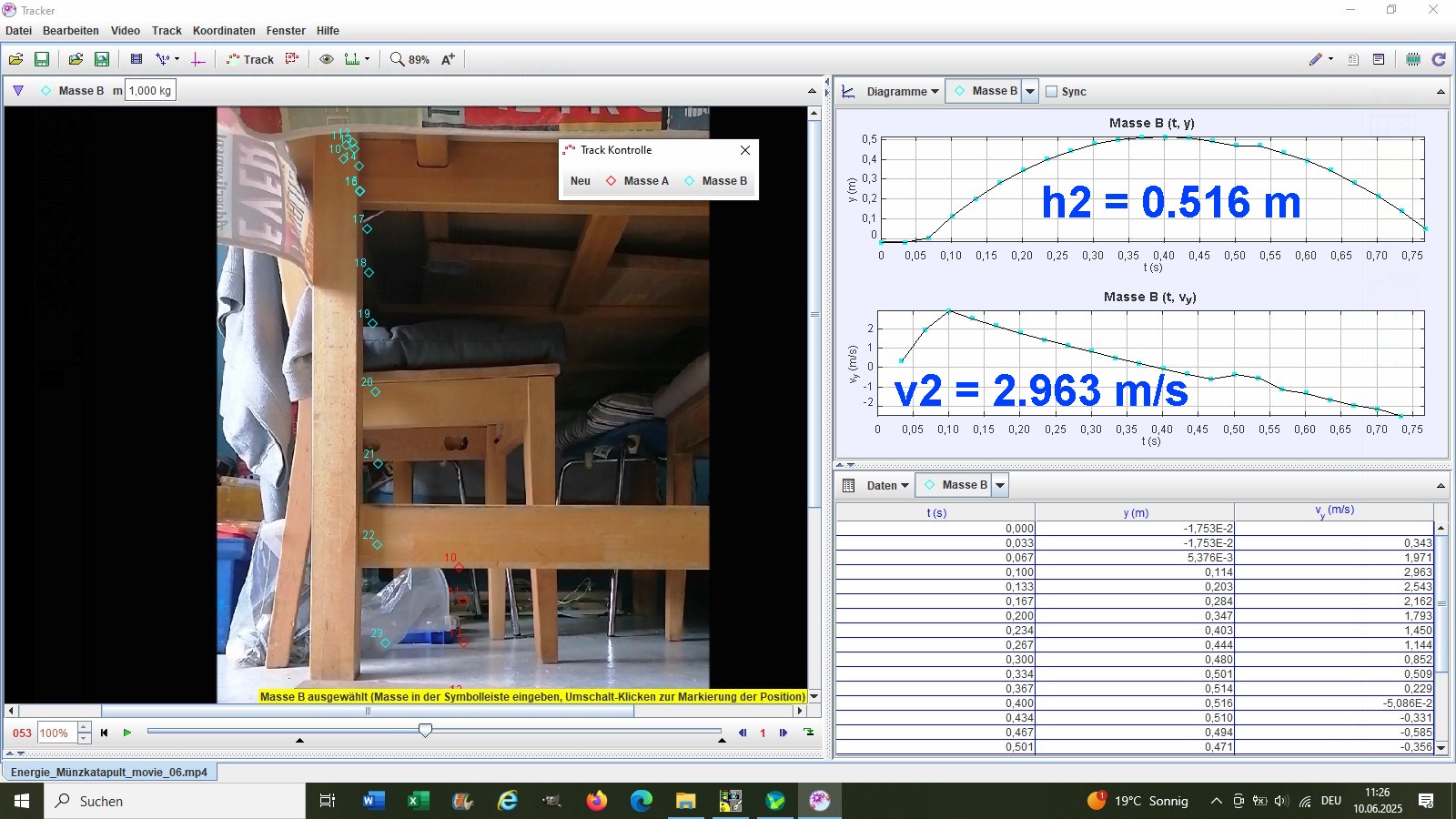
Die experimentell ermittelten Verhältnisse lauten: v2/v1 = 2.96/1.44 = 2.06 (Sollwert = 2) bzw. h2/h1 = 0.516/0.154 = 3.35 (Sollwert = 4). Theorie und Experiment liegen also nicht zu weit auseinander, Heureka 😉
Der Spritzenkocher
Für dieses Experiment benötigt man ein kleine Kunststoffspritze, Wasser, eine Kerze oder Brenner und eine Zange. Zuerst füllt man die Spritze zu ca. 30% mit Wasser. Dabei sollte sich nahezu keine Luftblase im Wasser befinden!


Hier erkennt man die Wasserfüllmenge bzw. die nur sehr kleine Luftblase:


Mit einer Kerze bzw. einem Brenner erhitzt man die Spritzenspitze, sodass diese weich wird. Danach quetscht man sie schnell mit einer Zange zusammen. Das in der Spritze befindliche Wasser ist nun luftdicht eingeschlossen.


Zieht man jetzt die Spritze mit der Hand auf, vergrößert sich das Volumen der Luftblase. Hat man alles richtig gemacht, müsste das Wasser in der Spritze zu sieden beginnen…



Hier der Bildausschnitt mit den sich bildenden Siedebläschen:

Wie kann dies aber sein, nachdem das Wasser ja keine 100 °C besitzt? Dazu müssen wir uns ein wenig mit dem sog. Dampfdruck einer Flüssigkeit/von Wasser beschäftigen. Die schnellsten Teilchen können nämlich eine Flüssigkeit verlassen und bilden über der Flüssigkeit ein Gas mit dem sog. Dampfdruck aus:

Dieser Dampfdruck hängt sehr stark von der Temperatur T der Flüssigkeit/des Wassers ab. Mit zunehmenden T wächst er sehr stark an/exponentiell an:

Bei T = 100 °C beträgt der Dampfdruck von Wasser 1 bar. Jetzt fällt einem bestimmt ein, dass Wasser ja auch bei 100 °C siedet. Es gibt in der Tat einen ganz engen Zusammenhang zwischen dem Dampfdruck und der Siedetemperatur einer Flüssigkeit. Und zwar siedet eine Flüssigkeit dann, wenn der Dampfdruck gleich dem äußeren Druck ist. Auf Meereshöhe herrscht ca. ein Druck von 1 bar. Deshalb muss Wasser auf Meereshöhe auf 100 °C erhitzt werden, bis es siedet. Denn dann beträgt der Dampfdruck = äußerer Druck = 1 bar.
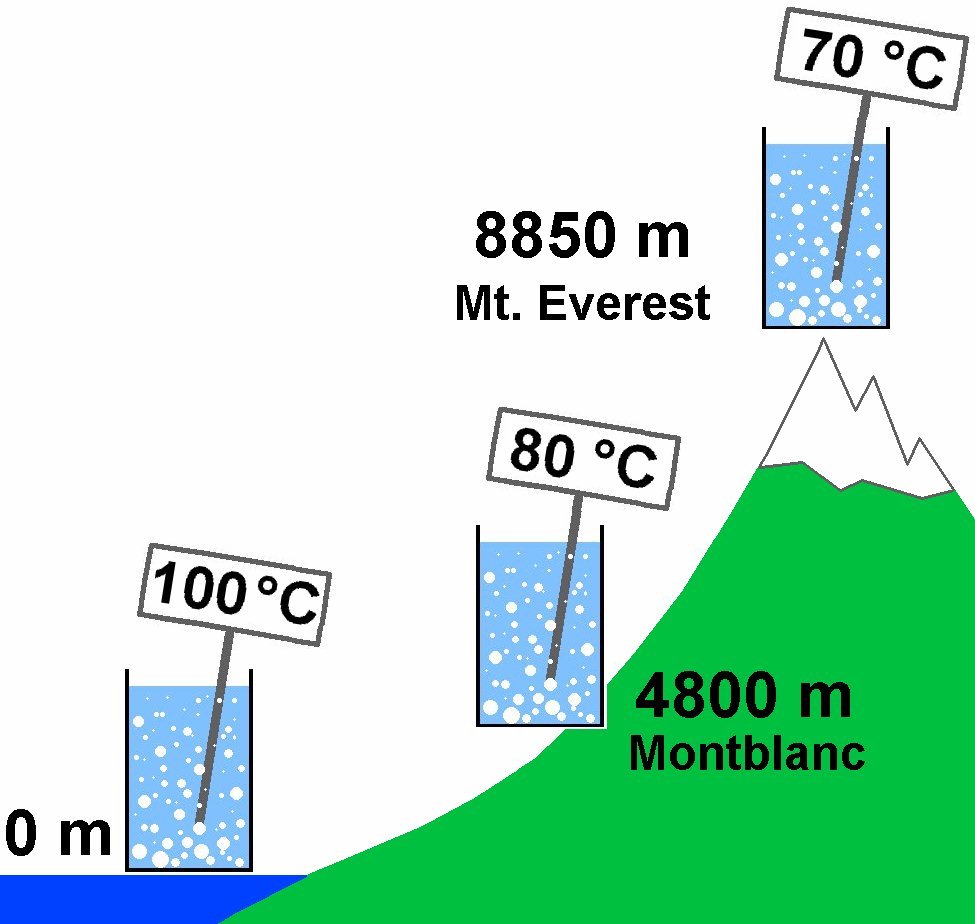
Auf dem Mount Everest herrscht nur noch ein Luftdruck von ca. 300 mbar. Erhitzt man auf seinem Gipfel Wasser, so beginnt dieses bereits bei nur 70 °C zu kochen. Der Grund ist einfach: Durch den geringeren Luftdruck erreicht das erhitzte Wasser bereits bei geringerer Temperatur die Forderung Dampfdruck = äußerer Druck. Man kann weiters daraus schließen, dass der Dampfdruck von Wasser bei 70 °C eben genau 300 mbar beträgt.
Im sog. Phasendiagramm sieht man diesen Umstand auch sehr gut:


Bei dem Experiment mit der Spritze wird aber nicht die Temperatur erhöht. Stattdessen wird der Luftdruck innerhalb der Spritze durch die Expansion erniedrigt. Ein doppeltes Volumen V bedingt ja einen nur noch halb so großen Druck p (vgl. Boyle-Mariotte-Gesetz). Angenommen das Wasser besitze eine Temperatur von 20 °C. Der Dampfdruck von Wasser bei 20 °C beträgt nur noch 23 mbar. Wird nun die Spritze so lange aufgezogen, bis der Luftdruck in ihr unter diese 23 mbar fällt, so beginnt das nach wie vor kalte Wasser zu sieden. Denn auch dann gilt wieder die Siedebedingung Dampfdruck = äußerer Druck!

Die implodierende Getränkedose
Auch dieser Versuch erklärt sich über den Dampfdruck von Wasser. Benötigt werden eine leere Getränkedose, eine Zange, eine kleine mit Wasser gefüllte Wanne und ein Bunsen- oder Flambierbrenner.

Man schüttet ein wenig Wasser in die leere Getränkedose. Dieses erhitzt man mit den Brenner, bis es siedet:


Tritt Wasserdampf durch das kochende Wasser aus der Dosenöffnung, dreht man die Dose schnell kopfüber und taucht sie ins kalte Wasser. Die Dose implodiert daraufhin in beeindruckender Art:




So sieht die komplett eingedrückte Dose am Ende aus:

Warum ist dies so? Nun, wir wissen durch den vorherigen Versuch „Spritzenkocher“, dass der Dampfdruck von Wasser bei 100 °C genau 1 bar beträgt. Durch das in der Dose kochende Wasser füllt sich diese nahezu komplett mit Wasserdampf mit einem Druck von eben 1 bar. Hält man nun die Dose ins kalte Wasser, so kühlt das Wasser abrupt ab. Der Dampfdruck sinkt dadurch ebenfalls sofort extrem stark ab.

Der sich bildende starke Unterdruck innerhalb der Dose führt zur Implosion. Der Dampfdruck nimmt durch die Temperaturabnahme sogar deutlich schneller ab als ein Gas, welches man um den selben Wert abkühlt (vgl. Gasgesetz p ≡ T). Denn die Teilchen des Wasserdampfs bewegen sich durch die Abkühlung nicht nur langsamer, sondern es treten auch viele Gasatome in die flüssige Phase über. Dadurch sinkt der Druck quasi doppelt!
Es folgen noch weitere spannende Freihandexperimente…

