
Unter Dispersion versteht man in der Physik die Abhängigkeit einer physikalischen Größe von der Frequenz f. So hängt etwa der Brechungsindex n von der Frequenz f, also von der Farbe des Lichts ab. Dies führt etwa bei einem Prisma zur bekannten Lichtaufspaltung in die einzelnen Regenbogenfarben und auch der Regenbogen verdankt seine Farben der Dispersion des Brechungsindex von Wasser.
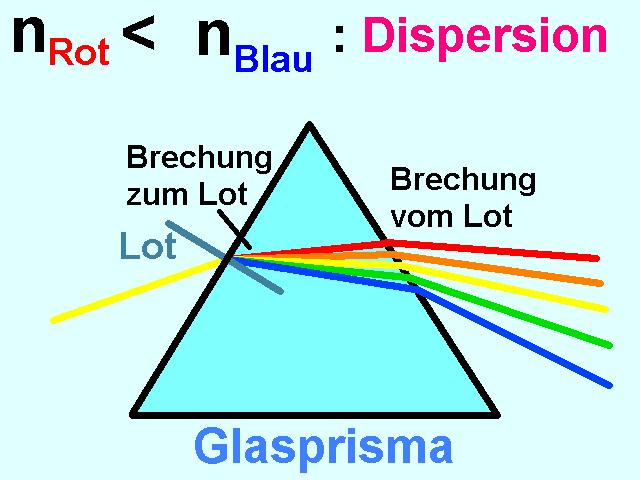
Während die Dispersion bei einem Prisma in einem Spektroskop erwünscht ist, möchte man sie bei optischen Linsen vermeiden, da sie zu einem Abbildungsfehler, der sog. chromatischen Aberration führt.
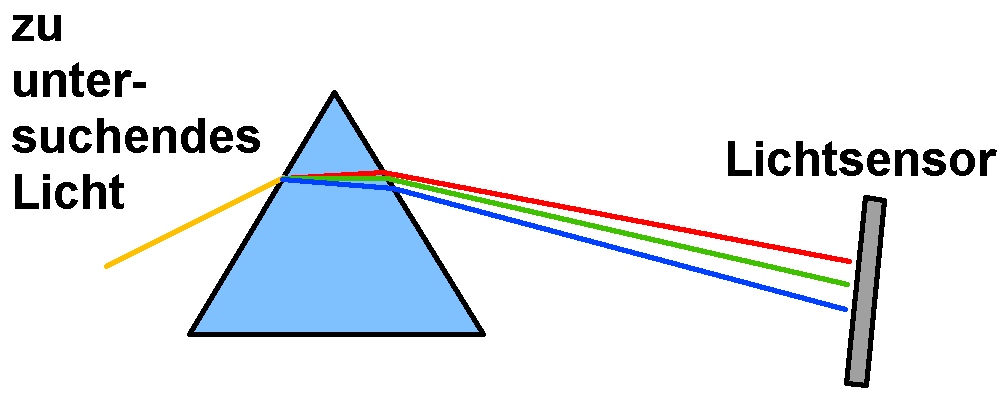
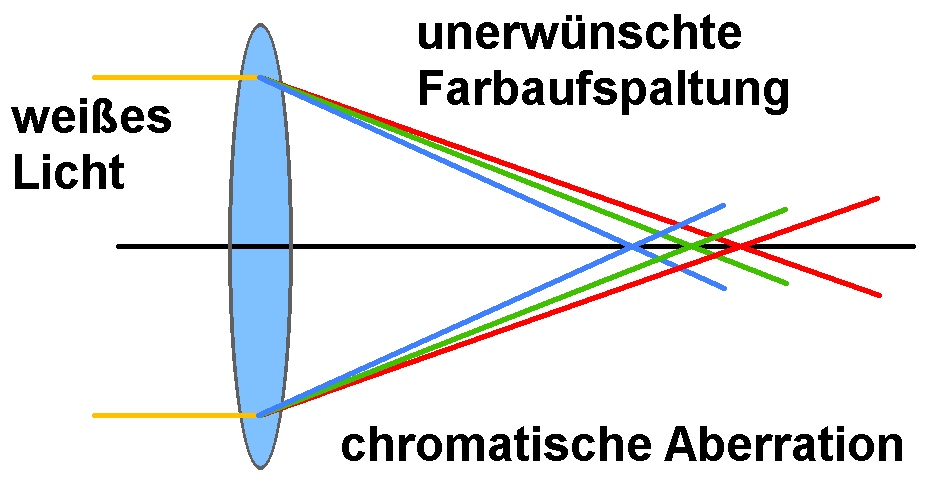
Wie man sieht, besitzt Flintglas eine stärkere Dispersion als Kronglas, da die Farbaufspaltung beim Flintglas größer ist:

Die bei Linsen unerwünschte Farbaufspaltung (chromatische Aberration):
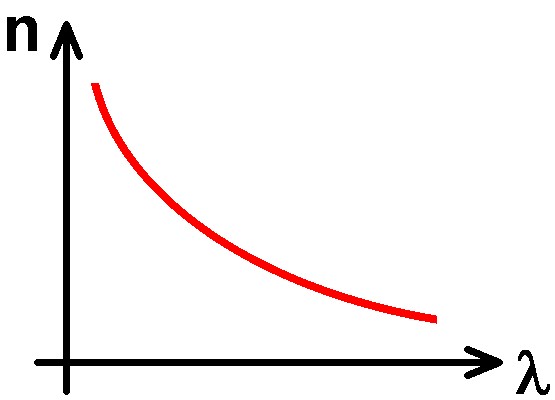
Bei einer normalen Dispersion gilt für den von der Wellenlänge/Farbe abhängigen Brechungsindex n: n(blau) > n(rot). Blaues Licht wird also stärker gebrochen als rotes. Bei der Beugung am Gitter war es genau umgekehrt. Die Dispersionskurve n(λ) sieht für die normale Dispersion in etwa wiefolgt aus:
Genau diese Kurve n(λ) möchte ich für Acrylglas experimentell bestimmen. Dazu habe ich mir ein günstiges Optikset auf Amazon besorgt:



Eigentlich war ich nur an diesem Halbkreis aus Acrylglas interessiert:

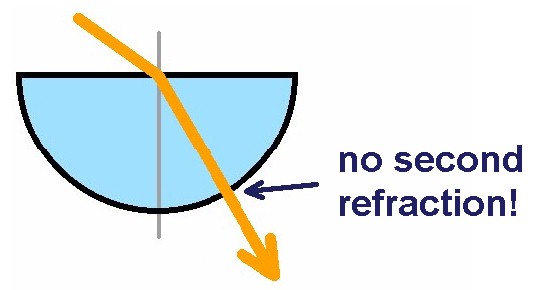
Trifft ein Laserstrahl auf diesen Halbkreis mit den Brechungsindex n, so wird er durch den Übergang optisch dünn zu optisch dicht zum Lot gebrochen. Der Halbkreis hat den Vorteil, dass es beim Austritt des Laserstrahls zu keiner neuerlichen Brechung kommt:
Für die Lichtbrechnung gilt das Snelliussche Brechungsgesetz:
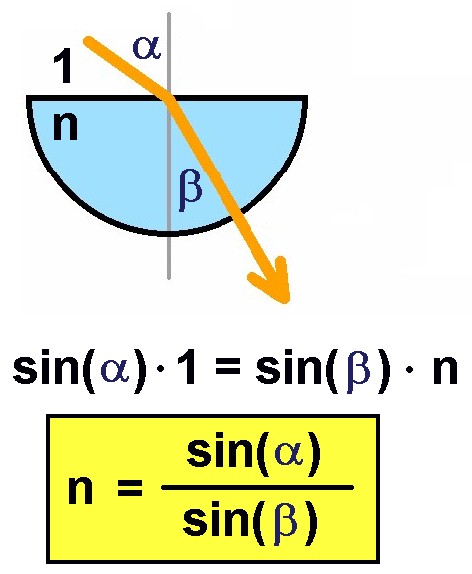
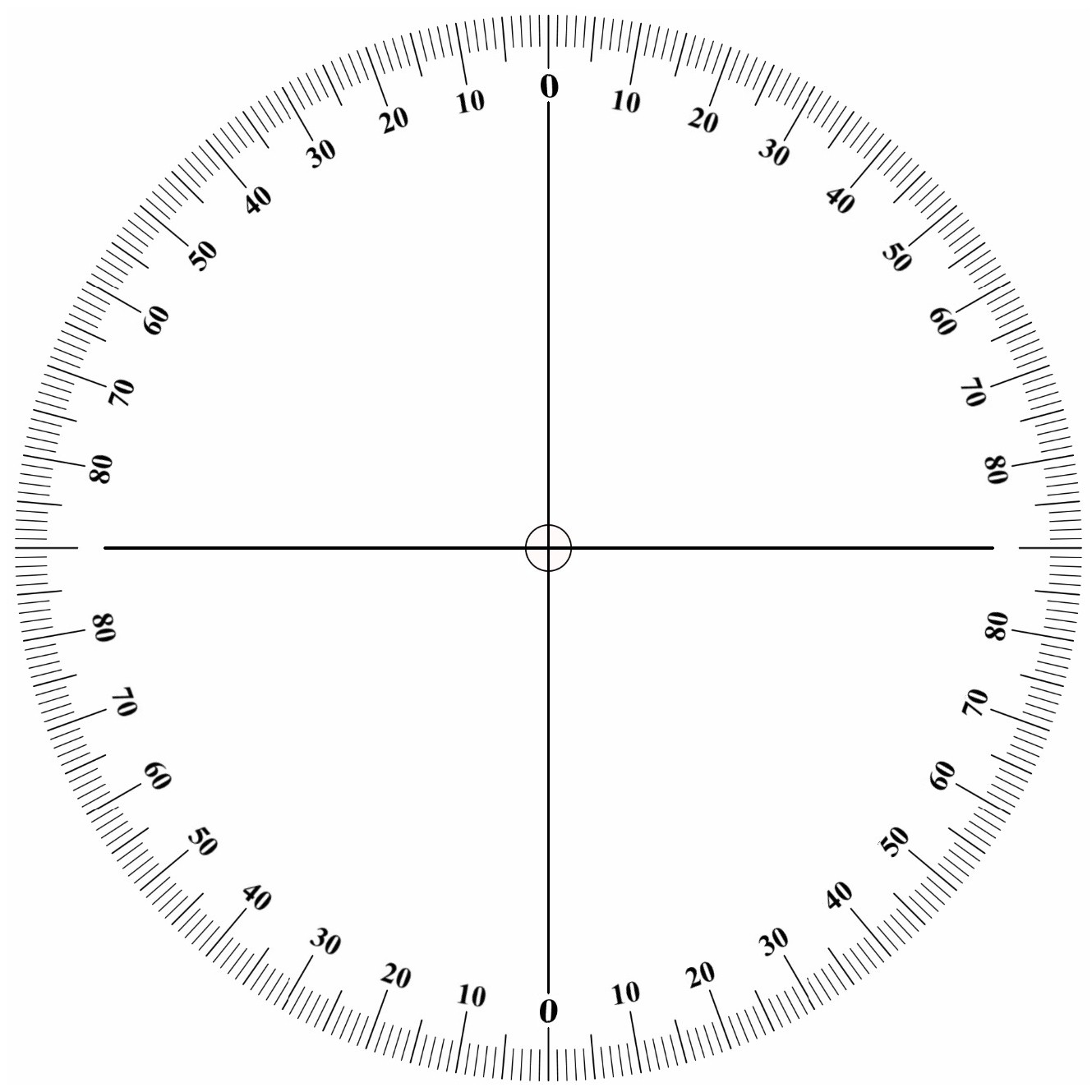
Durch Messung des Einfallswinkel α und des Ausfallswinkel β kann man den Brechungsindex n ermitteln. Zum bequemen Ablesen der Winkel habe ich mir eine Winkelschablone ausgedruckt:


Ich möchte ja den Brechnungsindex n für verschiedene Wellenlängen (Farben) bestimmen. Zum Einsatz kommen daher meine verschiedenfärbigen Laser:



Es gibt auch eine Gleichung für die Funktion n(λ), die sogenannte Cauchy-Gleichung. Zu dieser antwortete mir ChatGPT:

Die zu erwartende Dispersion ist leider allerdings sehr gering. Im Internet habe ich nach Dispersionskurven von Acrylglas recherchiert:
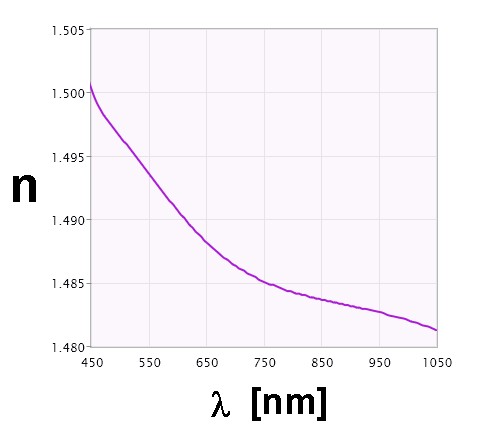
Quelle: https://www.filmetrics.de/refractive-index-database/Acrylic/Acrylate-Lucite-Plexiglass
Wie man anhand des Graphen erkennen kann, ändert sich der Brechungsindex n zwischen 450 nm (blau) und 750 nm (beginnendes Infrarot) nur um 0.015. Das ist sehr wenig und ich weiß nicht, ob ich das experimentell erfassen werde können.
Bei einem Einfallswinkel an Luft (n ≈ 1) von zum Beispiel α = 60° erhalte ich theoretisch folgende Ausfallswinkel:
Für n = 1.505: β = 35.26°
Für n = 1.485: β = 35.67°
Dieser geringe Winkelunterschied würde bei einem Kreisradius von r = 15 cm nur einem Bogen von lediglich 1.06 mm entsprechen…
So, mittlerweile habe ich mich ans Experiment gewagt. Um die Winkelauflösung zu erhöhen, versuchte ich es zunächst mit einer weit vom Acrylglashalbkreis entfernten Skala. Um diese zu kalibrieren habe ich den Linienlaser noch ohne Acrylglaskörper auf Winkel zwischen 30° und 40° ganz genau eingestellt und am Papier dann die entsprechenden Linien gezogen:


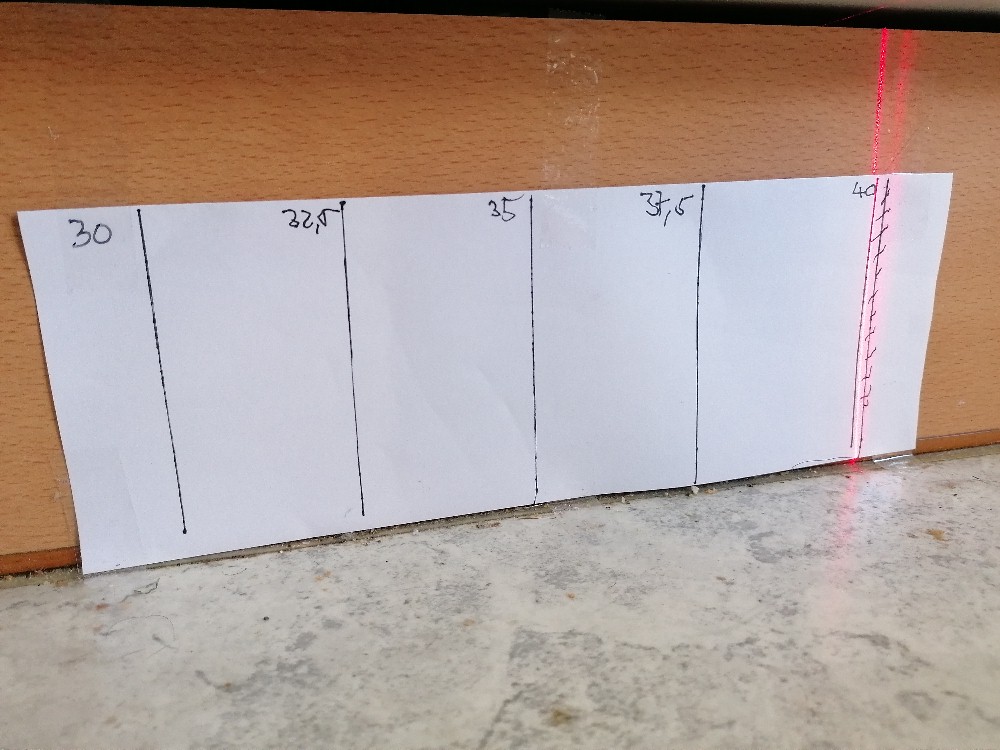
Danach klebte ich den Acrylglaskörper mit doppelseitigen Klebeband schön mittig auf meine kleinere Skala und beleuchtete diesen unter einem fixen Einfallswinkel von α = 60°:

Ich hoffte nun, auf der weit entfernten Skala eine Laserlinie zu erhalten. Indes bot sich mir folgendes Bild:

Anstelle einer halbwegs scharfen Linie war ein riesiger diffuser Klecks zu sehen. So konnte ich den Brechungswinkel in keinster Weise bestimmen, schade. Daher musste ich mich mit der kleineren Skala begnügen, welche natürlich eine wesentlich geringere Winkelauflösung besitzt.
Zuerst kam der rote 650 nm Laser zum Einsatz:



Der Brechungswinkel β lag bei etwas über 35°. Zur genaueren Bestimmung komme ich später noch…

Dann folgte der grüne Laser mit λ ≈ 520 nm:




Jetzt lag der Brechungswinkel bei ziemlich genau 35°:

Nun mein Cyan-Laser mit λ = 488 nm:




Der Brechungswinkel hat im Vergleich zum grünen Laser nur minimal abgenommen:

Zum Abschluss der 405 nm Laser:




Jetzt lag der Brechungswinkel schon etwas weiter unterhalb von 35°:

Wie man sieht und wie zu erwarten war, lagen die Brechungswinkel β für alle vier Laser extrem knapp beisammen. Zur Auswertung verwendete ich das Programm Tracker. Ich zog auf den Bildern zunächst eine weiße Linie genau entlang der Laserstrahllinie.
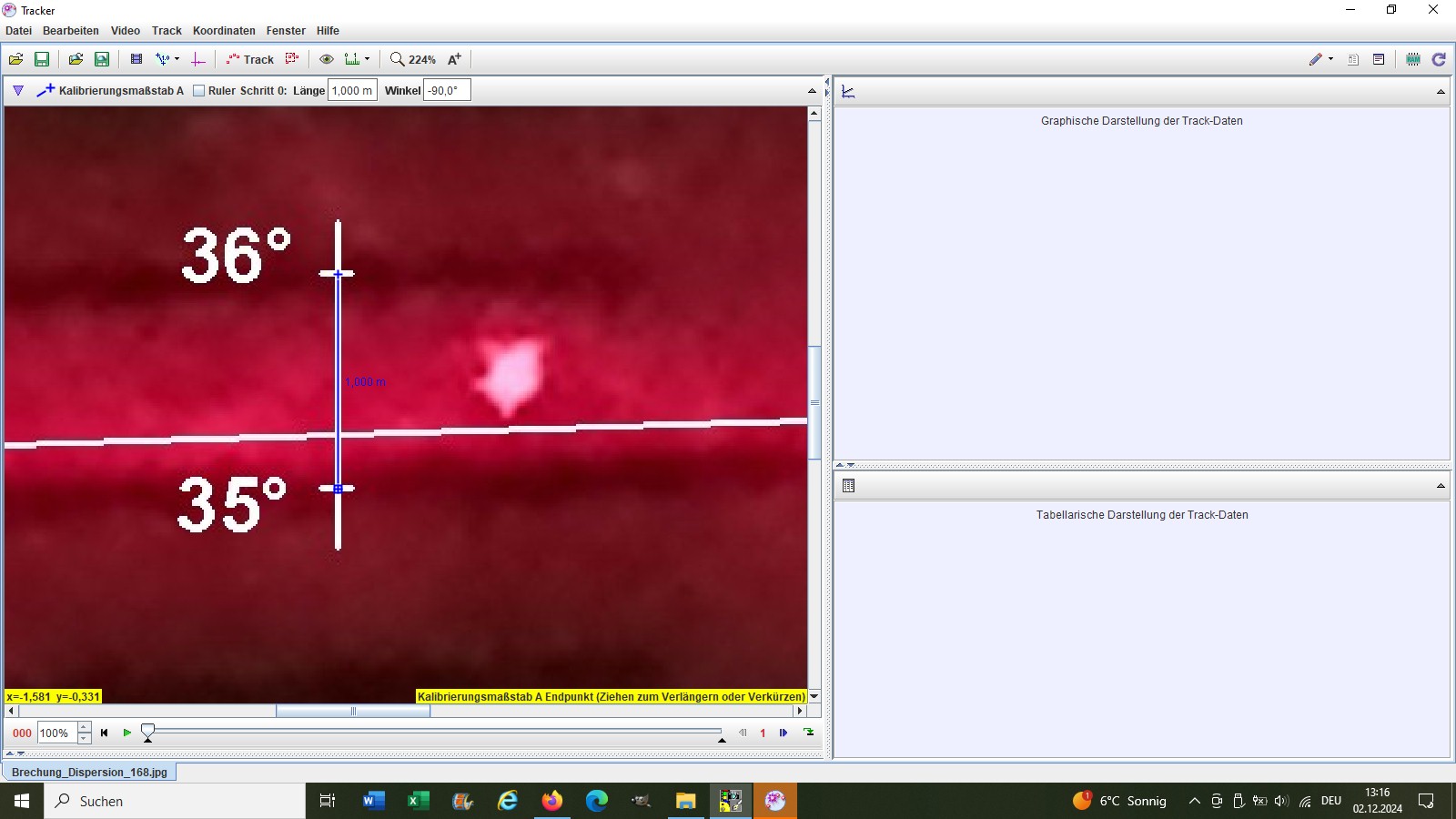
Danach zeichnete ich in den entscheidenden Bildausschnitt eine kurze vertikale weiße Linie und markierte die vollen Winkel (z.B. 35° und 36°):

Jetzt kalibrierte ich in der Software Tracker die Strecke zwischen den beiden Winkel mit der Länge 1:
Danach setzte ich den Koordinatenursprung in die untere Markierung und las dann die y-Koordinate des Schnittpunkts mit der „Laserstrahllinie“ ab. Für den roten Laser kam ich so auf einen Brechungswinkel von β = 35.245°. Links unten im Bild erkennt man die entscheidende y-Koordinate 0.245.
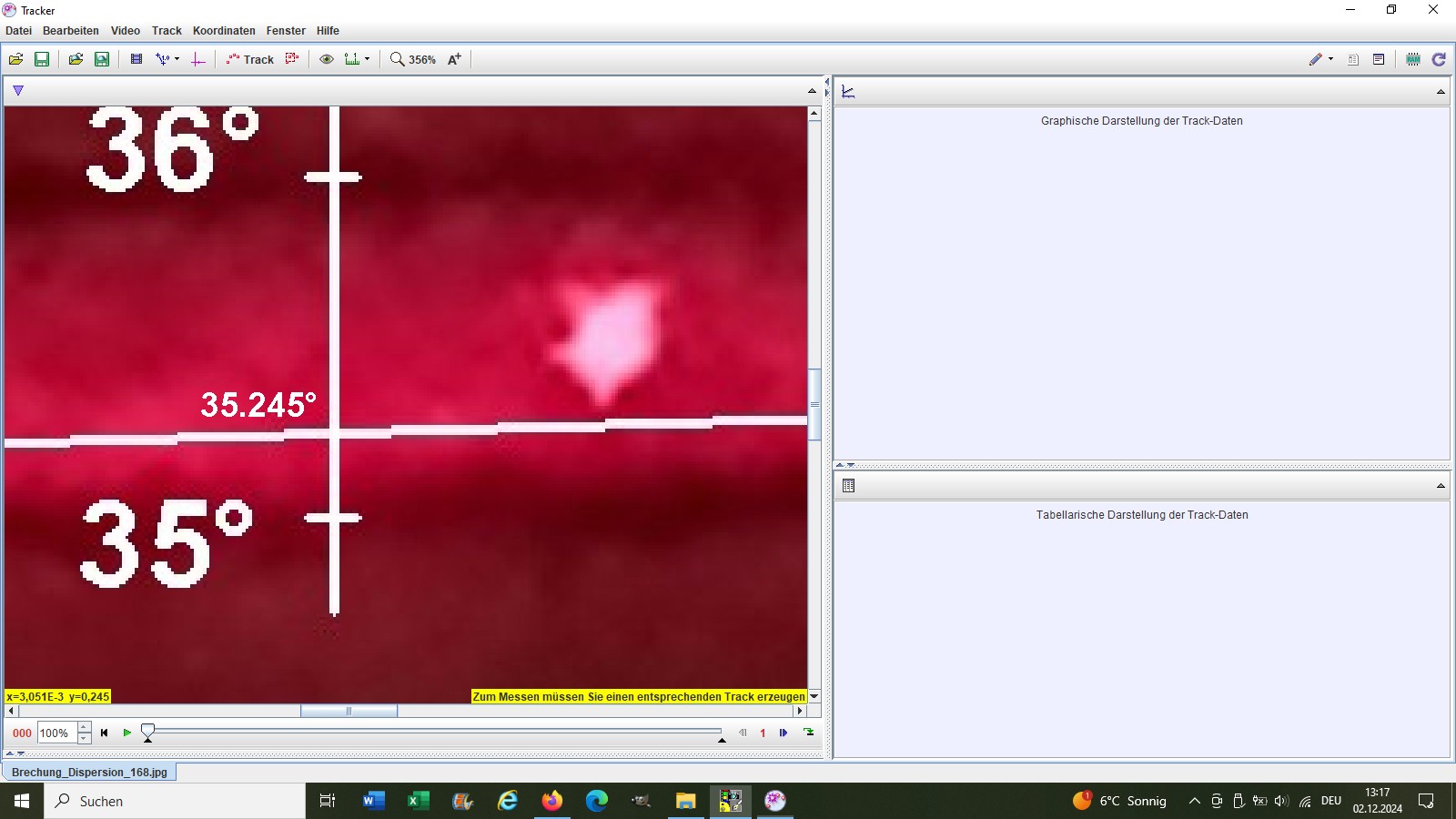
Dies wiederholte ich mit den drei anderen Laser:
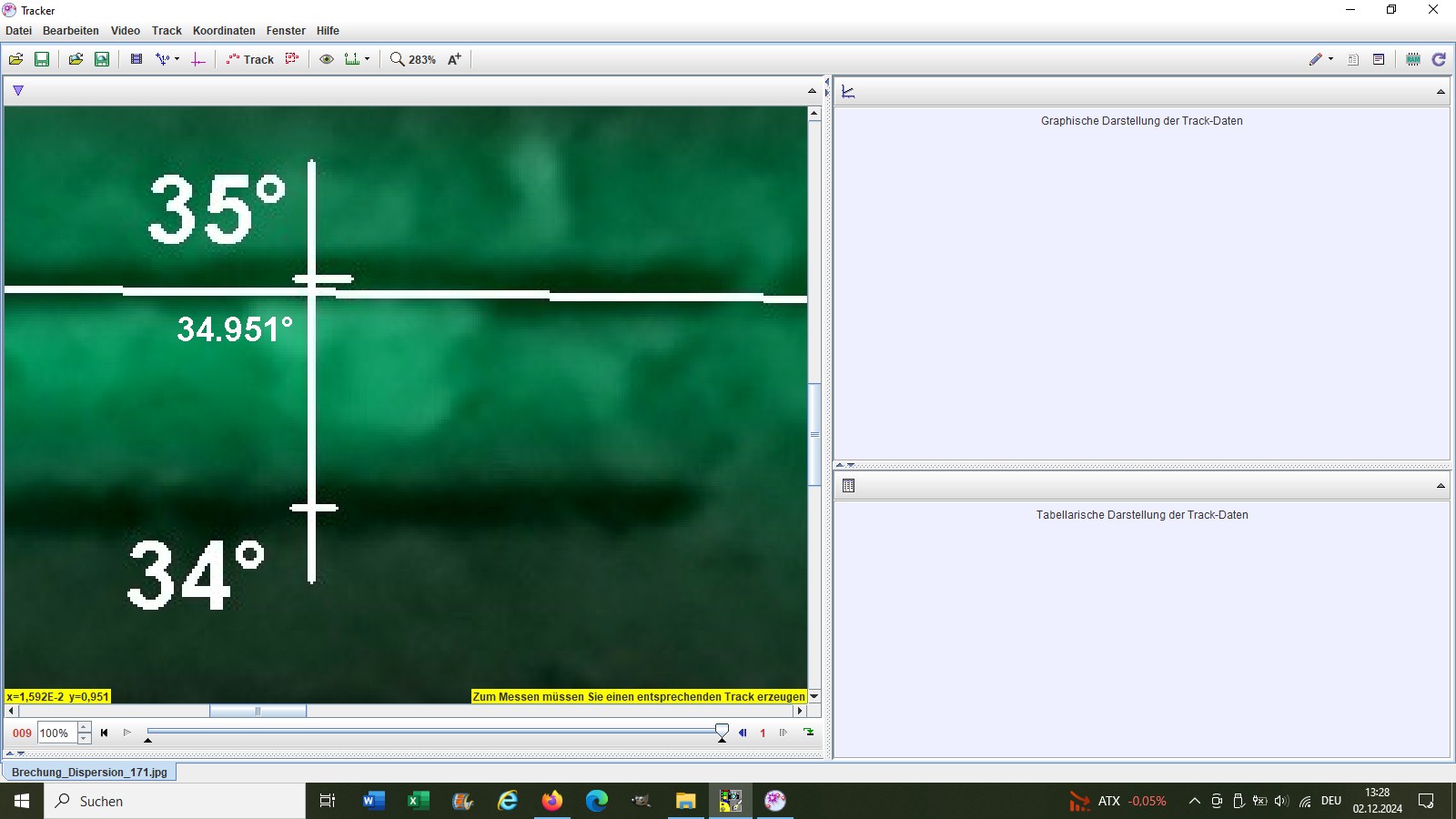
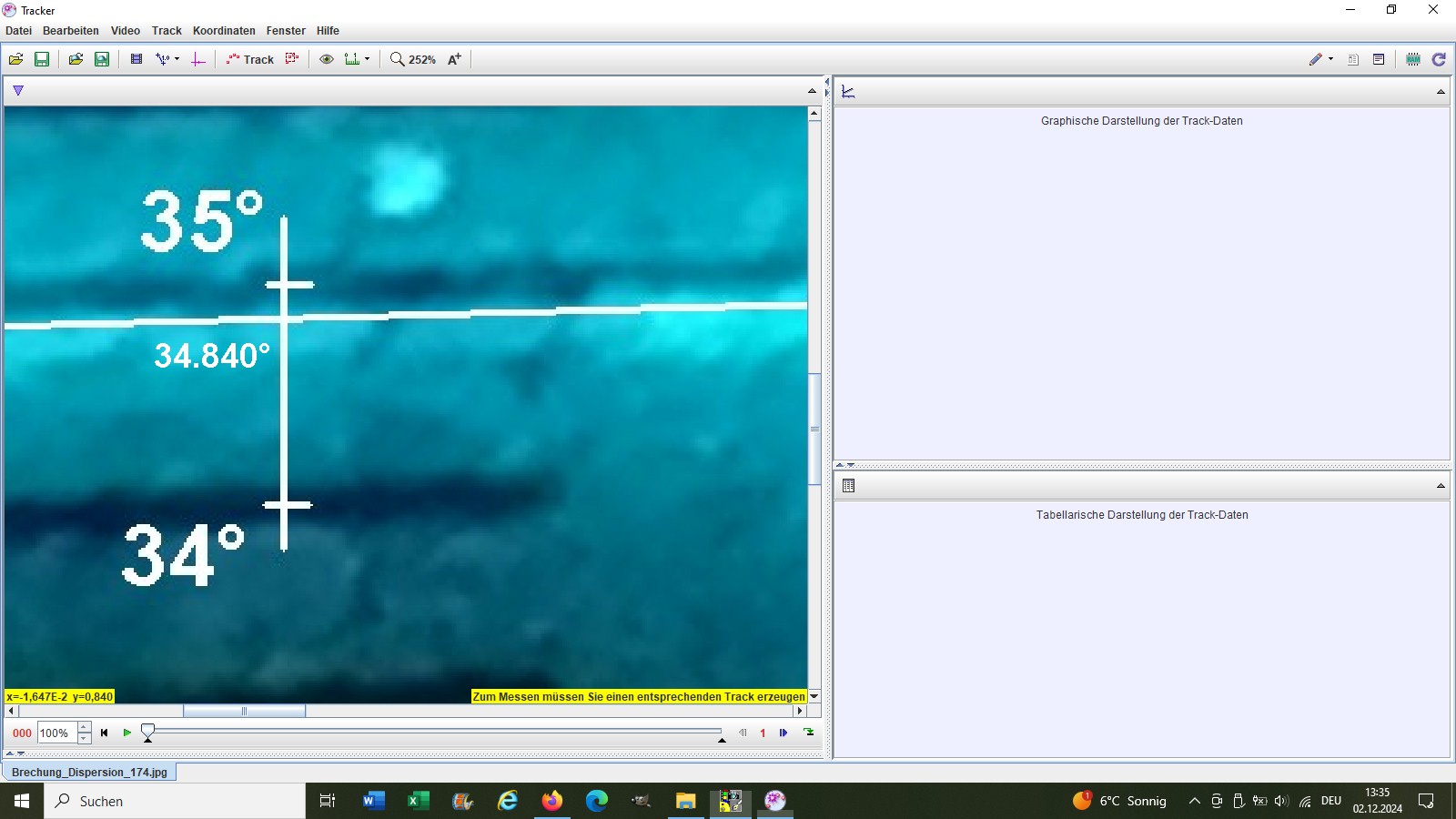
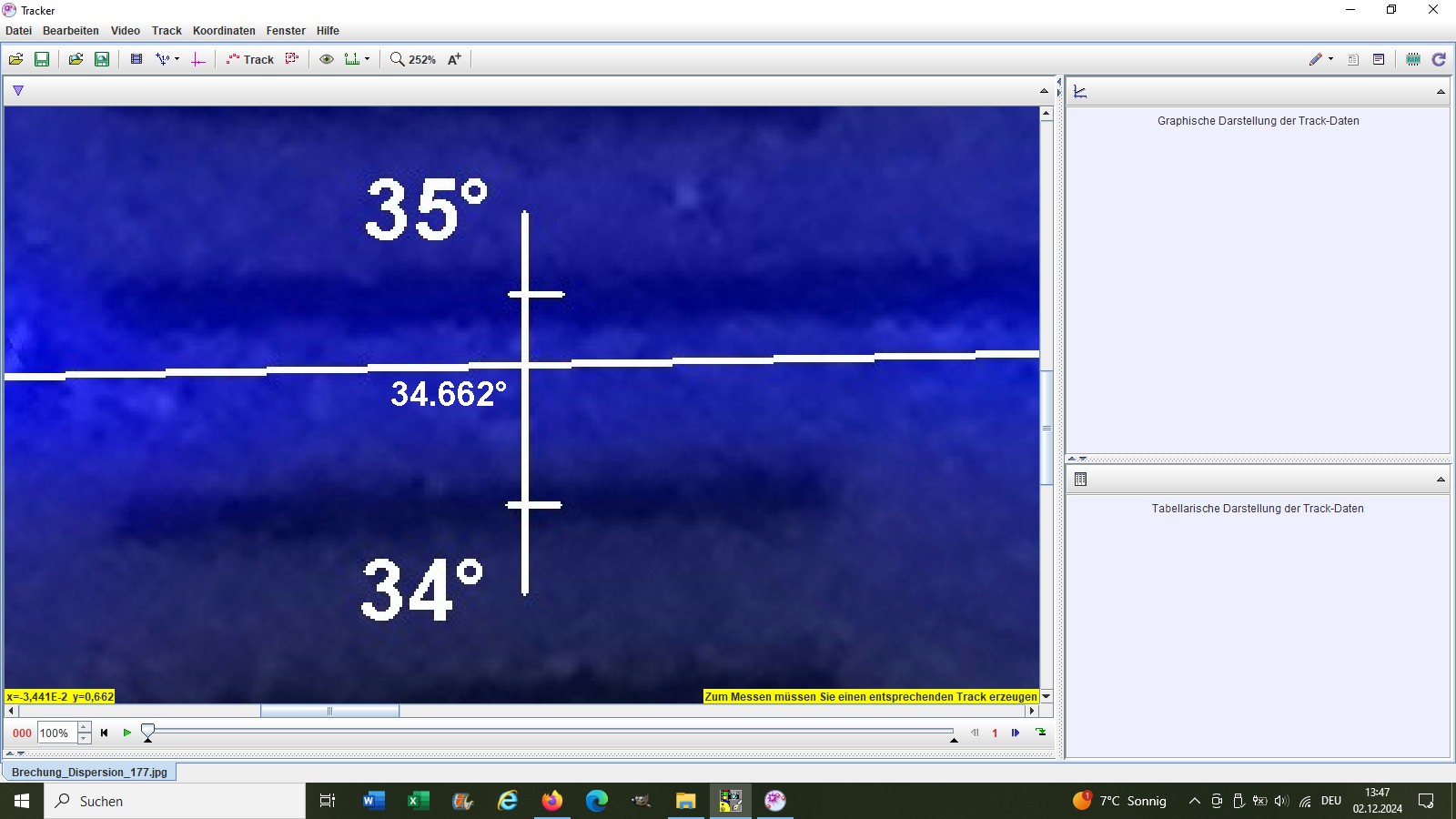
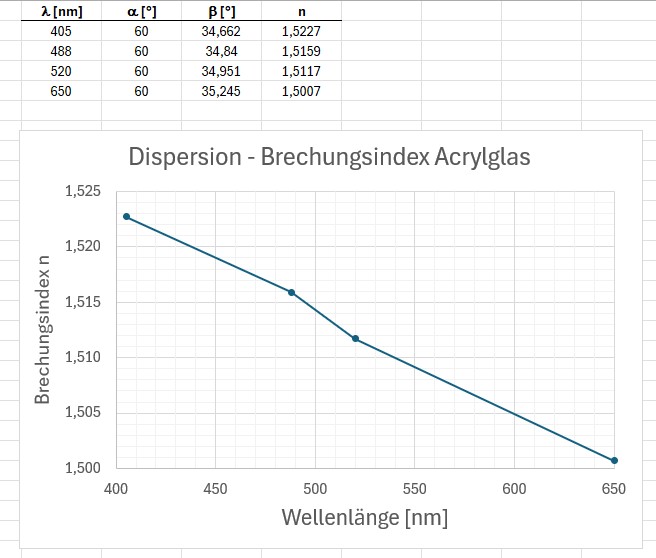
Hier nun die Ergebnisse für die Brechungswinkel β und die daraus ermittelten Brechzahlen n bzw. meine Dispersionskurve n(λ):
Weiter oben habe ich bereits erwähnt, dass es eine Gleichung für die Dispersionskurve n(λ) gibt und zwar die Cauchy-Gleichung. Hier nochmals die Antwort von ChatGPT:

Diese Funktion habe ich mir von EXCEL zeichnen lassen:
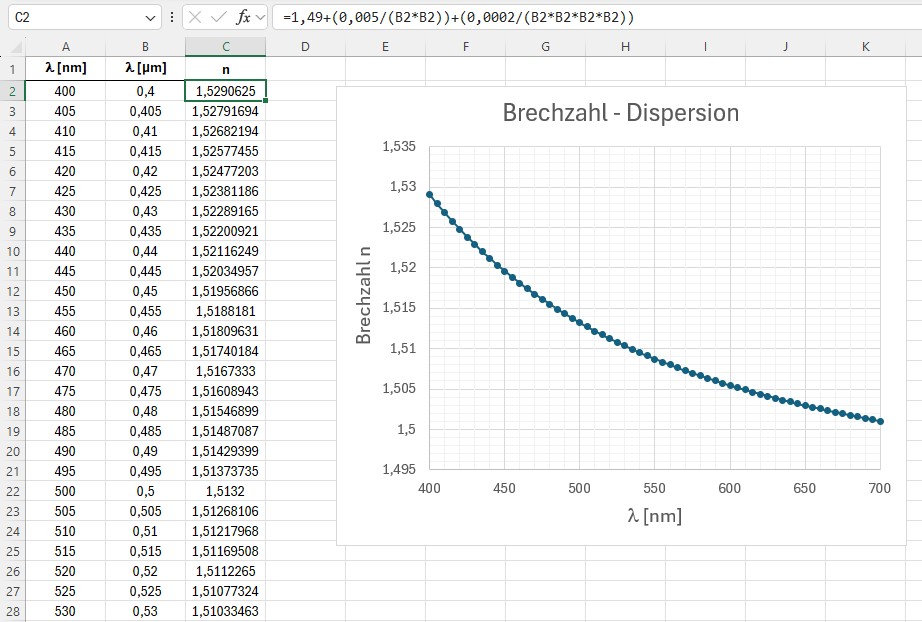
Lege ich nun diese theoretische Kurve über meine experimentell erhaltene, so ergibt sich folgendes Bild:
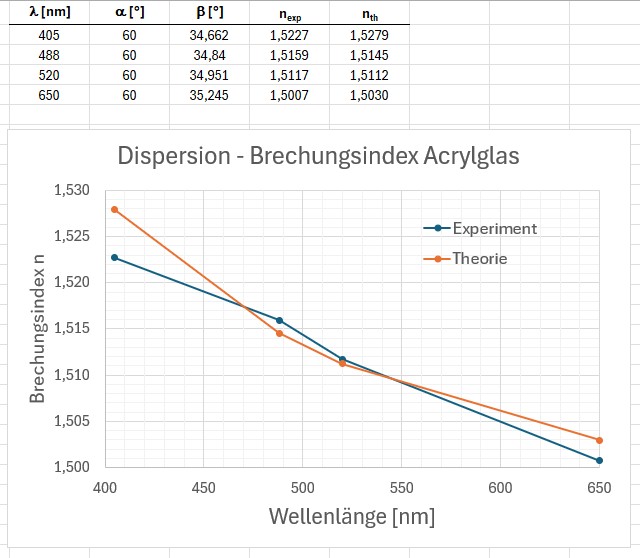
Ich war hocherfreut und erstaunt zugleich ob der sehr guten Übereinstimmung. Man darf nicht vergessen, um welch geringe Winkelunterschiede es in diesem Experiment gegangen ist. Da kann ich nur wieder laut rufen, Heureka 😉
Das dazugehörige Youtube-Video reiche ich wie immer nach…

