
Bildquelle: https://de.wikipedia.org/wiki/Gaspard_Gustave_de_Coriolis#/media/Datei:Gaspard-Gustave_de_Coriolis.jpg, public domain
Die Corioliskraft ist eine der drei Trägheitskräfte der klassischen Mechanik, die in einem rotierenden Bezugssystem auftreten. Sie tritt genau dann in Erscheinung, wenn ein Körper sich in einem rotierenden Bezugssystem bewegt und wenn diese Bewegung nicht parallel zur Rotationsachse bzw. zum Vektor der Winkelgeschwindigkeit ω verläuft. Die beiden anderen Trägheitskräfte im rotierenden Bezugssystem, Zentrifugalkraft und Eulerkraft, wirken auch dann, wenn der Körper im rotierenden Bezugssystem ruht. Die Corioliskraft ist nach Gaspard Gustave de Coriolis (1792 – 1843) benannt, der sie in einer 1835 erschienenen Publikation ausführlich behandelte.
Die Formel für die Corioliskraft lautet:
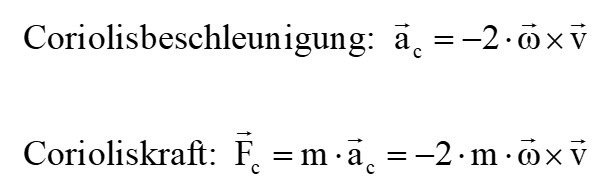
Sie steht somit normal auf den Winkelgeschwindigkeitsvektor ω (= Drehachse) und den Geschwindigkeitsvektor v.
Wo treten Corioliskräfte im Alltag auf? Die Erde ist ein drehendes Bezugssystem mit einer zwar kleinen Winkelgeschwindigkeit aber immerhin. Die Rotationsrichtung von Wirbelstürmen beruht etwa auf der Corioliskraft.

Bildquelle: Image Science and Analysis Laboratory, NASA-Johnson Space Center, public domain
https://eol.jsc.nasa.gov/SearchPhotos/photo.pl?mission=STS51I&roll=44&frame=52
Tiefdruckwirbel drehen sich etwa auf der Nordhalbkugel entgegen dem Uhrzeigersinn und auf der Südhalbkugel im Uhrzeigersinn.
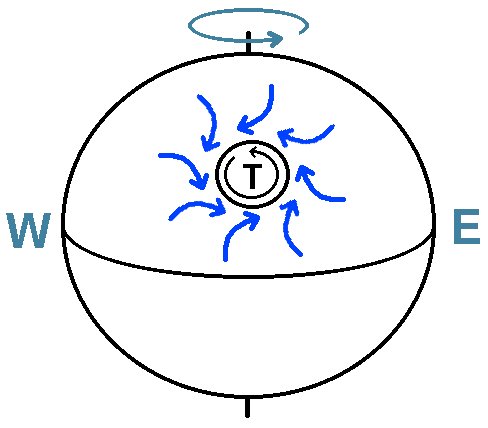
Oder nehmen wir einen sehr hohen Turm, von dem eine Kugel fallen gelassen wird. Wie wird sich diese aufgrund der Corioliskraft bewegen?
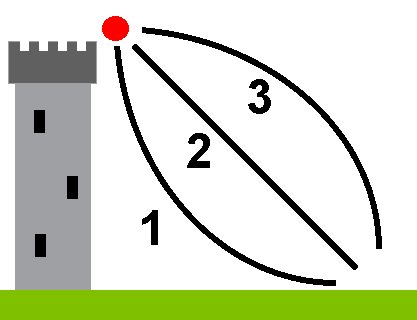
Es kommt in diesem Fall zu einer Ostabweichung. Man kann sich dies auch so erklären: Nehmen wir an, der Turm befände sich am Äquator. Dann besitzt der Fußpunkt des Turms durch die Erdrotation eine Geschwindigkeit vBoden = ωErde · rErde. ≈ 1600 km/h. Die Turmspitze ist aber geringfügig weiter vom Erdmittelpunkt entfernt und besitzt die Geschwindigkeit vSpitze = ωErde · (rErde + h). Lässt man nun die Kugel fallen, so hat sie quasi eine höhere Geschwigkeit als zum Mitkommen in geringerer Höhe notwendig wäre. Infolgedessen überholt sie die senkrecht unter dem Startpunkt befindlichen Orte. Die Bahn sieht dann stark übertrieben in etwa so aus:
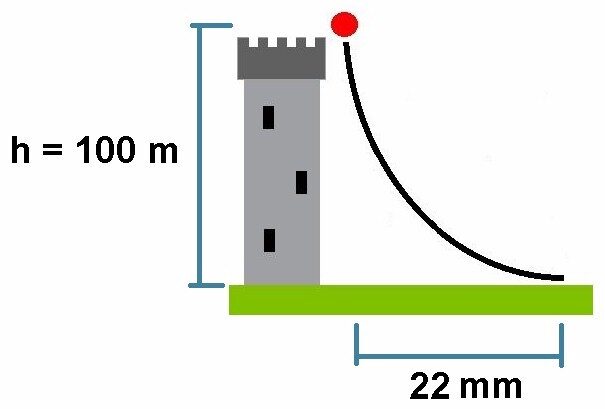
Bei einer Turmhöhe von 100 m beträgt die Ostabweichung nur ca. 22 mm. Hier die genaue Herleitung der Formel für die Ostabweichung:

Man hält es kaum für möglich, aber auch Scharfschützen müssen eigentlich die Corioliskraft berücksichtigen. Dazu eine kleine Rechnung: Entfernung zum Ziel = 800 m, Projektilgeschwindigkeit = 2000 km/h, Schuss exakt nach Norden bei einer geographischen Breite von 45°.

Die Abweichung von beachtlichen 5.9 cm durch die Corioliskraft ist also nicht zu vernachlässigen. Ein guter Scharfschütze so wie Mark Wahlberg im Film berechnet die notwendige Korrektur natürlich in Windeseile im Kopf 😉
Man beachte: Bei halber Projektilgeschwindigkeit ist die Abweichung durch die Corioliskraft sogar doppelt so groß. Denn die Coriolisbeschleunigung a ist dann zwar nur halb so groß, dafür die Flugzeit t doppelt so lang. Nach der Formel s = 1/2 · a · t² ergibt dies aber eine Verdopplung der Strecke s!
Wohin zeigt die Corioliskraft, wenn sich eine Kugel auf einer sich drehenden Scheibe nach innen bewegt?
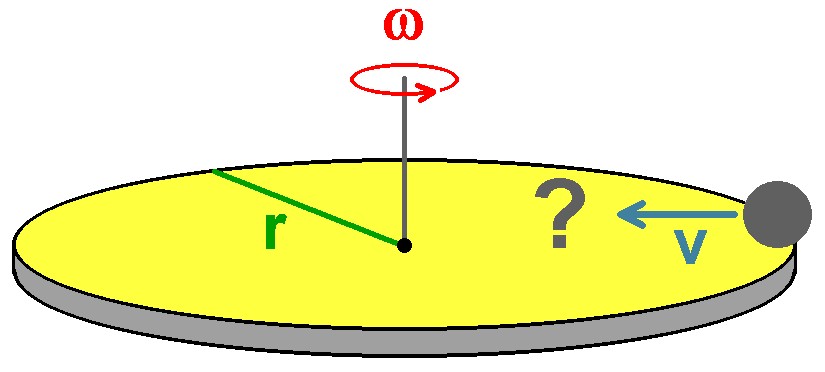
Der Kraftvektor der Corioliskraft zeigt ja in Richtung –(ω × v), also normal auf ω und normal auf v. Im obigen Fall erfährt die Kugel konkret eine Kraft nach rechts.

Sie wird infolge der Corioliskraft auch nicht die Mitte der Scheibe erreichen, sondern an ihr rechts vorbeirollen. Genau dies möchte ich experimentell überprüfen. Dazu habe ich mir einen großen, gebrauchten Drehteller gekauft:

Der gesamte Aufbau soll dann so aussehen:
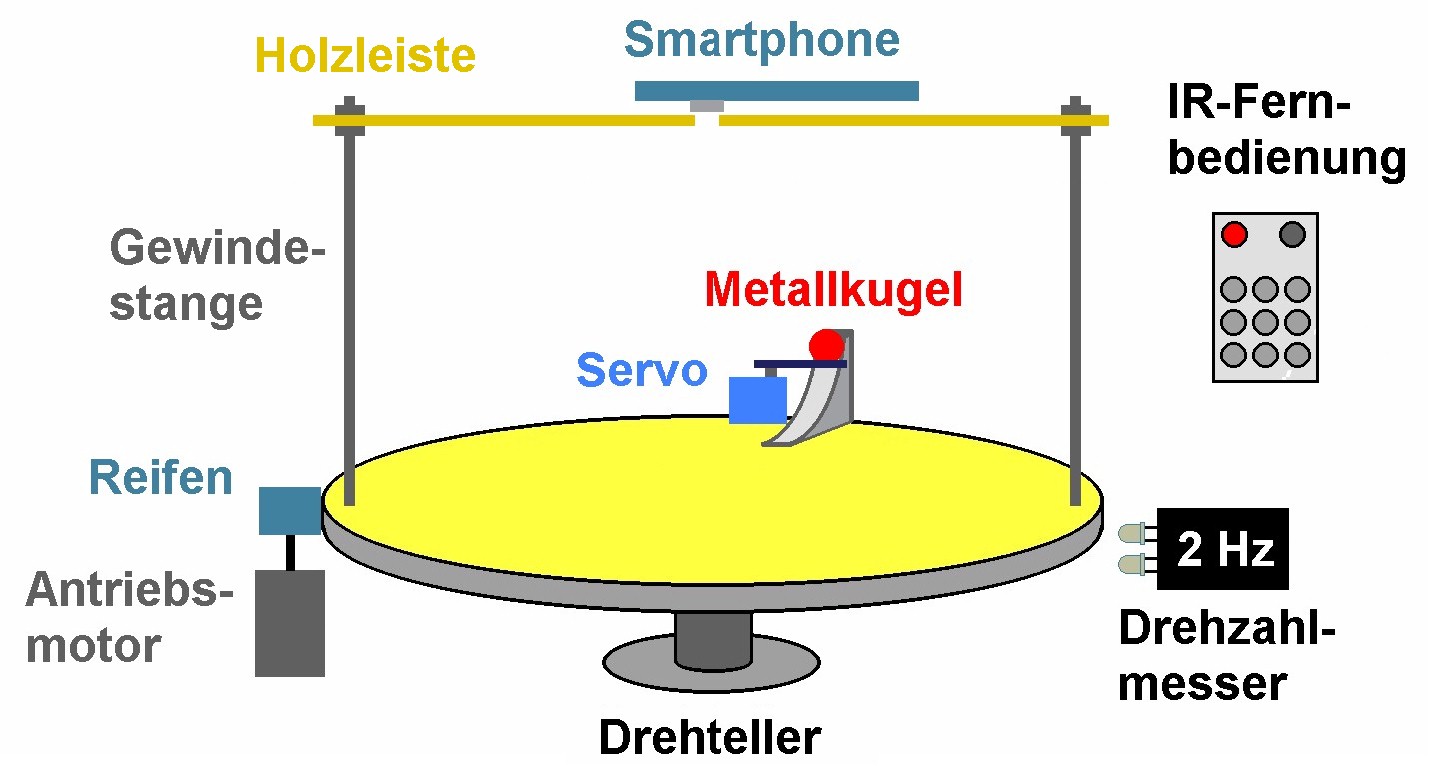
Am Rand werde ich eine kleine Kugelrampe montieren und mit dem mitbewegten Smartphone filme ich alles von oben. Man kann die Bahn der Kugel in Abhängigkeit von ihrer Startgeschwindigkeit v und der Winkelgeschwindigkeit ω des Drehtellers auch mit EXCEL simulieren. Hierfür habe ich ein kurzes „Programm“ geschrieben. Zunächst betrachten wir noch einmal die Formel für die Corioliskraft: Der Winkelgeschwindigkeitsvektor zeigt ja in die z-Richtung und lautet daher (0,0,ω). Für den Geschwindigkeitsvektor gilt ganz allgemein (vx,vy,0), da die Bewegung der Kugel ausschließlich in der horizontalen xy-Ebene erfolgt.

Man kann den Beschleunigungsvektor aufgrund der Corioliskraft auch durch folgende Überlegung herleiten: Die Coriolisbeschleunigung steht ja normal auf v und die z-Achse (ω-Vektor). Den Vektor v kann man ganz einfach um 90° nach rechts drehen, wenn man die x- und y-Koordinaten vertauscht und dann bei der neuen y-Koordinaten das Vorzeichen wechselt. Auf diese Weise kommt man auch zum Vektor der Coriolisbeschleunigung.
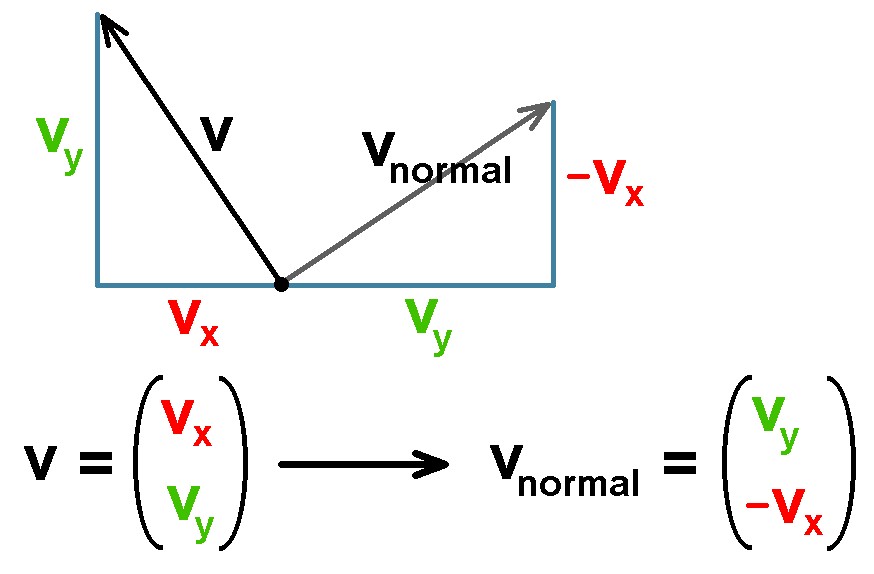
Den Beschleunigungsvektor aufgrund der Zentrifugalkraft habe ich oben auch gleich berechnet. Für die gesamte Beschleunigung ages der Kugel folgt daher:

Ich kenne jetzt also die x- und y-Komponente der Gesamtbeschleunigung. Die Beschleunigung a entspricht aber der zeitlichen Geschwindigkeitsänderung Δv/Δt. Bei bekanntem a und bekanntem Zeitschritt Δt kenne ich daher auch die Geschwindigkeitsänderung jeweils in x- und y-Richtung. Kenne ich die Geschwindigkeitskomponenten vor dem Zeitschritt, so kenne ich diese auch nach dem Zeitschritt.
Ist die aktuelle Geschwindigkeit v bekannt und auch die Länge des Zeitschritts Δt, so kann ich mir nach der bekannten Formel v = Δs/Δt aber die Ortsänderungen Δs in x- und y-Richtung berechnen. Kenne ich dann wieder die Orte vor dem Zeitschritt, so kenne ich den neuen Ort nach dem Zeitschritt. Zur Erhöhung der Genauigkeit dieser Simulation nehme ich für die Berechnung von Δs die mittlere Geschwindigkeit vor bzw. nach dem Zeitschritt. Ich gehe bei diesem sog. Euler-Verfahren wiefolgt vor:
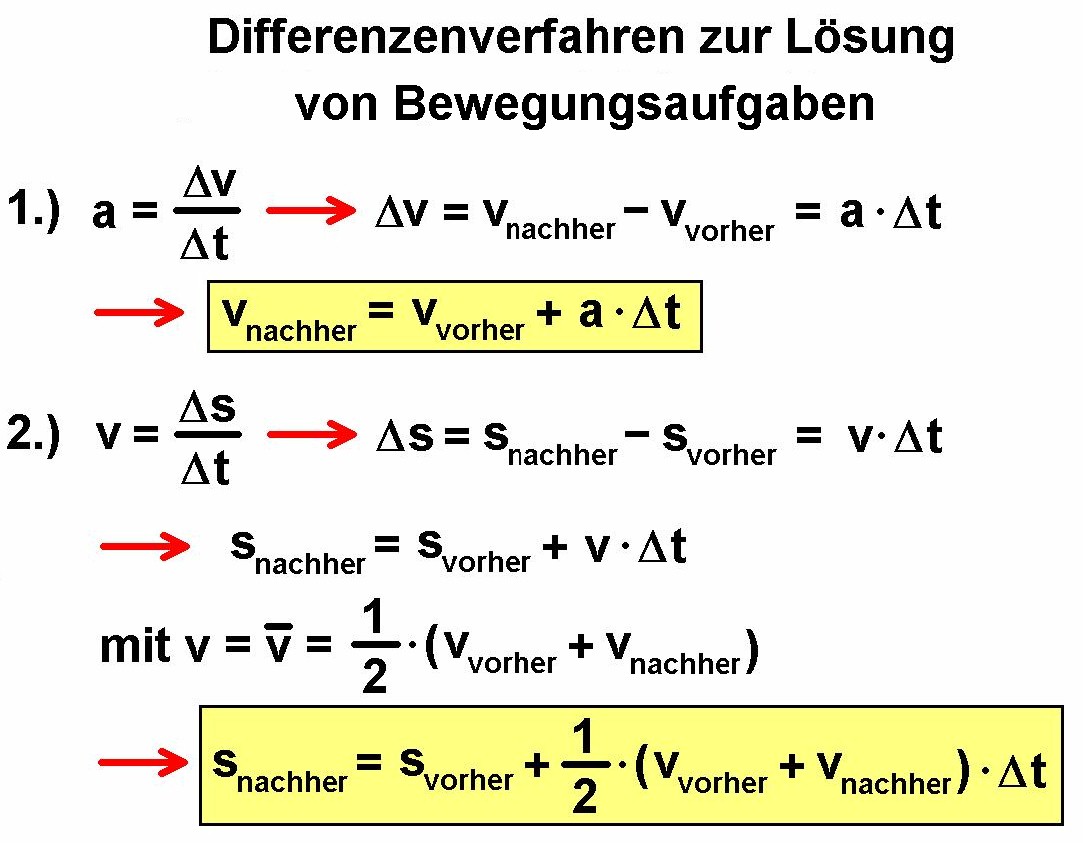
Alles was ich wissen muss, sind die Zeitschritte Δt, die Startbedingungen für Ort und Geschwindigkeit und dann die Beschleunigungen in x-und y-Richtung während der Bewegung. Auf diese Weise erhalte ich immer wieder die neuen Orte und Geschwindigkeiten nach den einzelnen Zeitschritten. Für diese Aufgabe ist EXCEL wie geschaffen. Hier die Oberfläche des „Programms“:
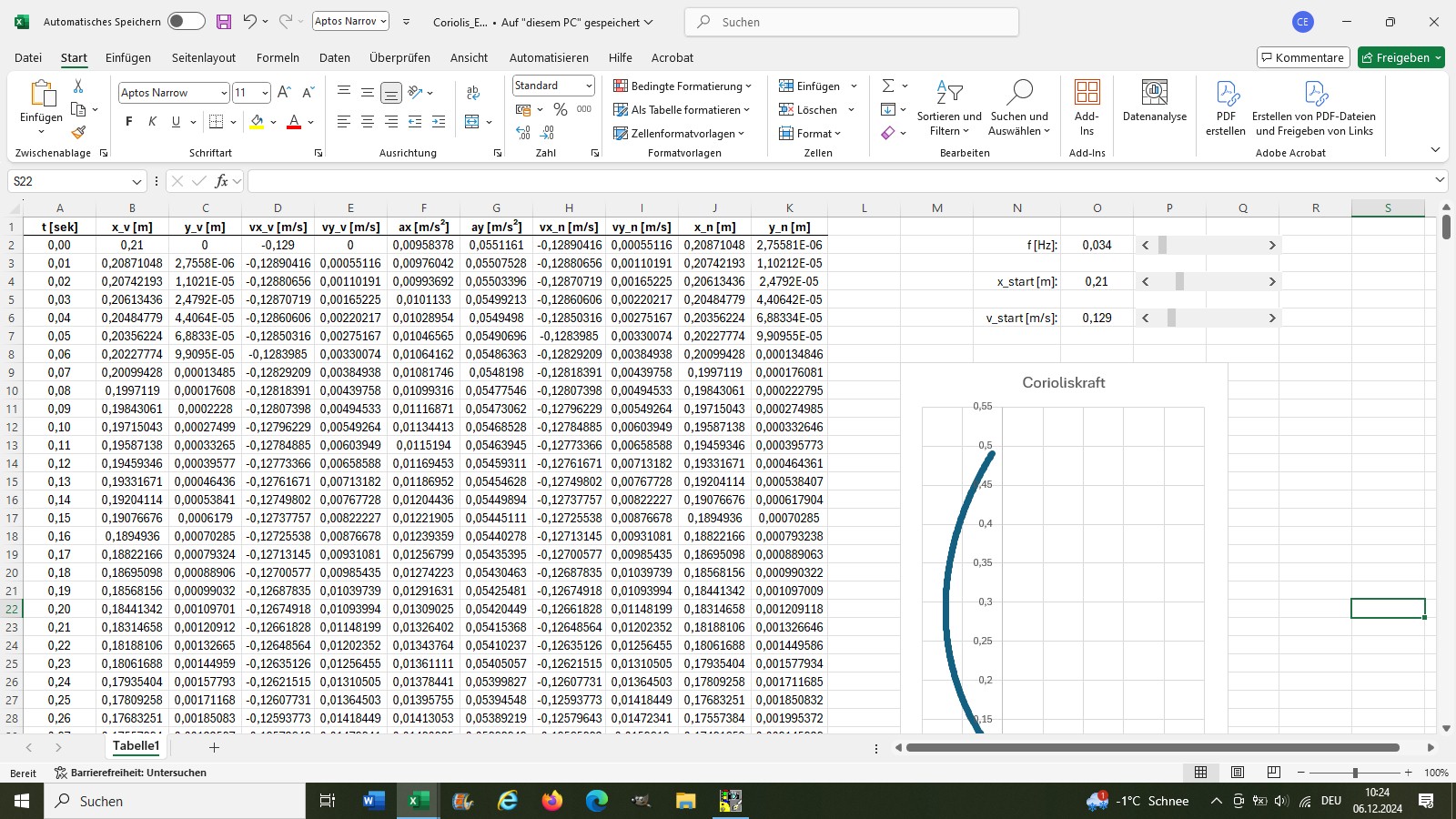
EXCEL-Datei: Coriolis_Excel
Eine typische Bahnkurve der Kugel auf dem Drehteller:
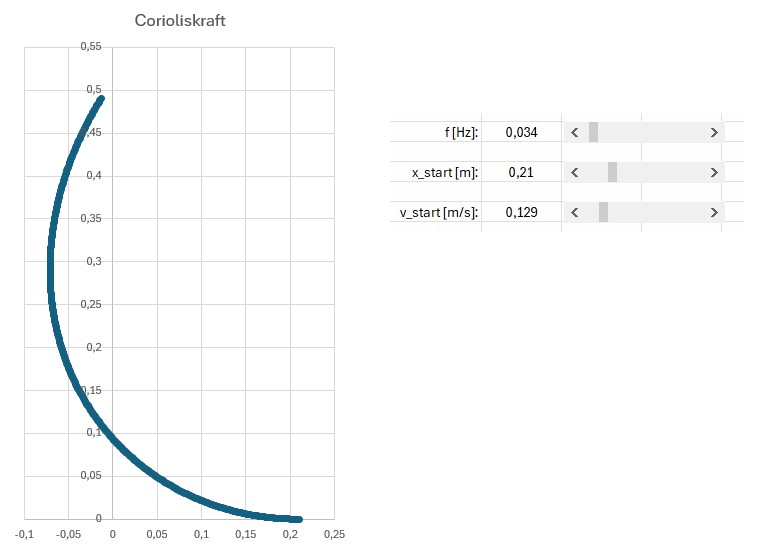
Wie man sieht, erreicht die Kugel nicht den Mittelpunkt (0,0) des Drehtellers, sondern rollt rechts an ihm vorbei. Ich möchte mit diesem Experiment aber nicht nur rein qualitativ diese Ablenkung zeigen, sondern auch quantitativ die Formel für die Corioliskraft bzw. -beschleunigung beweisen. Mit dem Smartphone nehme ich ja die Bewegung der Kugel von oben auf. Die Software Tracker gestattet es mir nun, diese Bewegung zu vermessen. Zu Beginn kurze Zeit nach dem „Einschießen“ der Kugel bewegt sich diese ja annähernd nur in negativer x-Richtung. Die Coriolisbeschleunigung zeigt demnach zu Beginn der Kugelbewegung weitestgehend nur in y-Richtung und ist auch annähernd konstant.
Für eine gleichmäßig beschleunigte Bewegung gilt aber der einfache Zusammenhang: s = 1/2 · a · t². Die Strecke s ist konkret die y-Position der Kugel nicht allzu lange nach Kugelstart. In der unten abgebildeten Simulation befindet sich die Kugel etwa nach t = 0.9 Sekunden bei der Stelle y = 0.022 m. Daraus lässt sich mit obiger Formel für die glm. Beschleunigung die Beschleunigung a bestimmen. Ich komme anhand der Bahnkurve auf einen Wert von ac = 0.054 m/s².
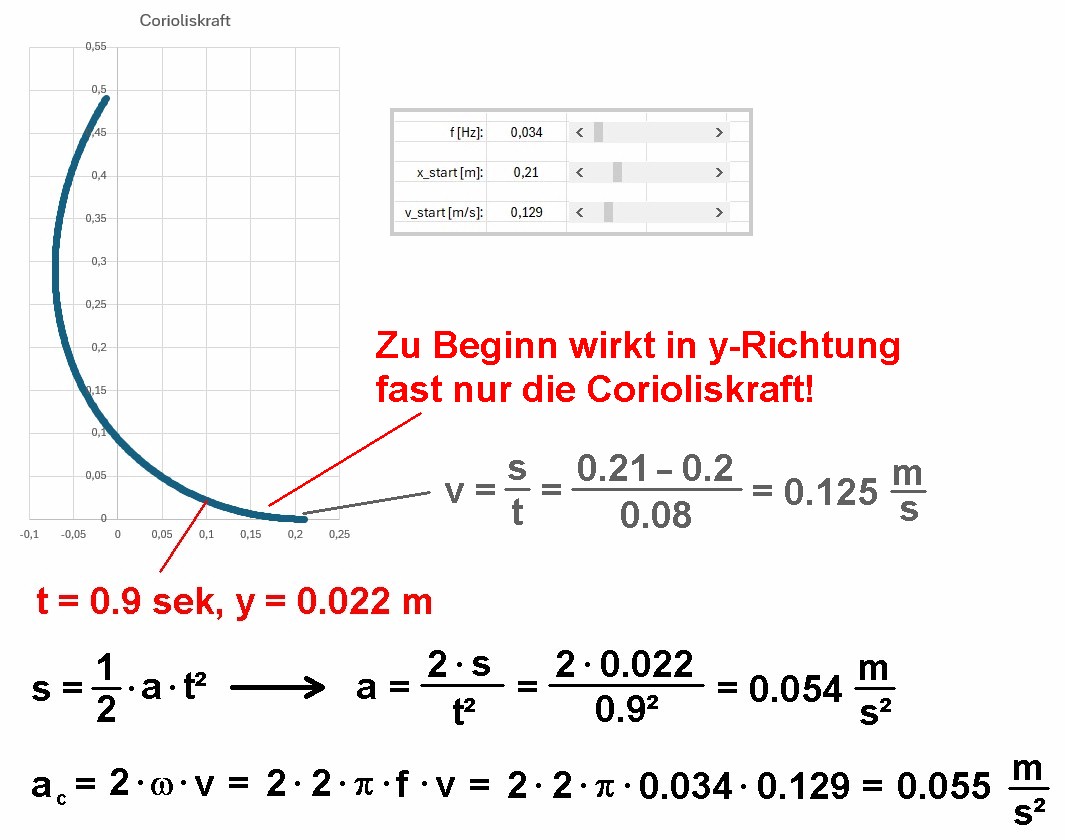
Ich möchte diesen experimentell ermittelten Wert für die Coriolisbeschleunigung aber auch mit der Theorie vergleichen. Laut dieser gilt ja für den Betrag der Coriolisbeschleunigung (= Betrag eines Vektor- bzw. Kreuzprodukts) : ac = 2 · ω · v · sin(Winkel zwischen ω und v) = 2 · ω · v · sin(90°) = 2 · ω · v.
Für die theoretische Berechnung von ac benötige ich also ω bzw. die Drehzahl f (Zusammenhang ω = 2 · π · f) und die Geschwindigkeit v. In der Simulation oben brauche ich diese Werte nur ablesen (f = 0.034 Hz, v = 0.129 m/s) und erhalte folgenden Theoriewert für die Coriolisbeschleunigung: ac = 0.055 m/s². Dieser Wert ist nahezu identisch mit jenem aus der Bahnkurve ermittelten, voila…
Im Experiment muss ich f des Drehtellers mittels Drehzahlmesser bestimmen und die Geschwindigkeit v anhand der Videoanalyse mit der Software Tracker. Aber so kann ich wunderschön Theorie und Praxis miteinander vergleichen.
Den Drehteller treibe ich seitlich mit einem starken Getriebemotor + Gummireifen an, wobei der Motor 228 rpm bei 12V macht. Aktuell kaufen musste ich ihn zum Glück nicht, da ich ihn schon vor längerer Zeit einmal für einen Balancierroboter angeschafft hatte…





Die Drehzahl f bestimme ich mit meinem Arduino-Drehzahlmesser (https://stoppi-homemade-physics.de/drehzahlmesser/):
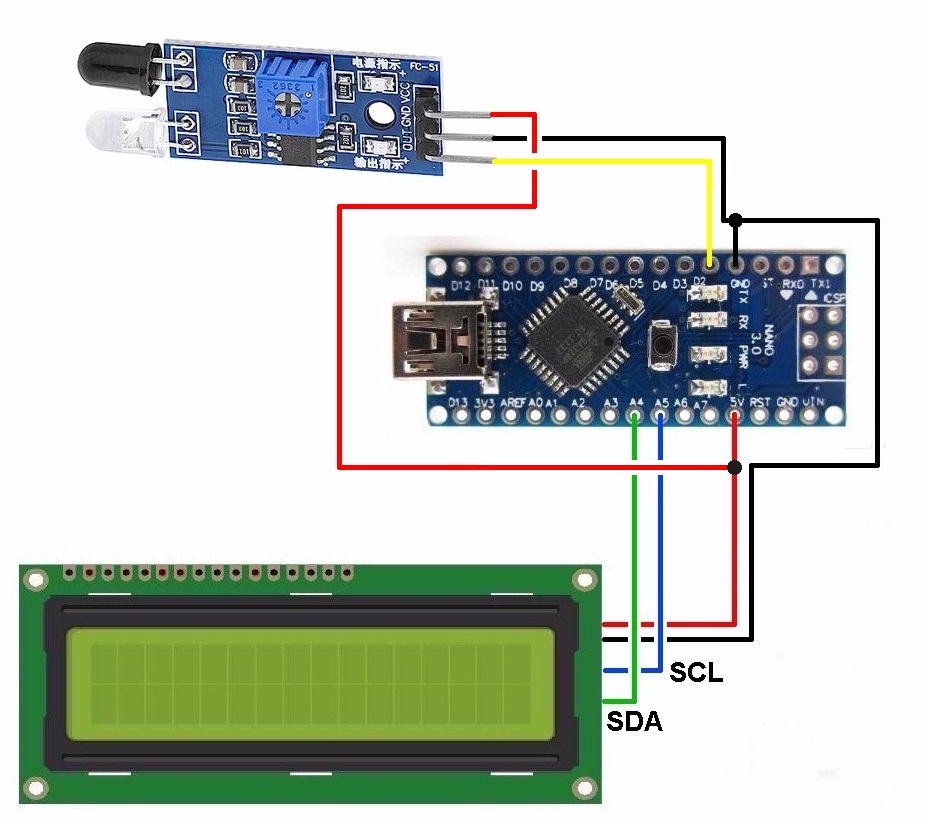



Der Arduino-Code für den Drehzahlmesser:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
#include <LiquidCrystal_I2C.h> #include <Wire.h> LiquidCrystal_I2C lcd(0x27,16,2); // set the LCD address to 0x27 for a 16 chars and 2 line display. ACHTUNG: Adresse kann auch 0x3F sein !!! // Anschlüsse: // GND - GND // VCC - 5V // SDA - ANALOG Pin 4 // SCL - ANALOG pin 5 int sensor = 2; unsigned long currentTime; unsigned long lastTime; //unsigned long pulse_freq; unsigned long period; float pulse_freq; // =========================== // ======= SETUP ========= // =========================== void setup() { pinMode(sensor, INPUT); Serial.begin(9600); attachInterrupt(digitalPinToInterrupt(sensor), pulse, FALLING); // Setup Interrupt lcd.begin(); // initialize the lcd lcd.backlight(); lcd.setCursor(0,0); lcd.print("Drehzahl-"); lcd.setCursor(0,1); lcd.print("messer"); delay(3000); lcd.setCursor(0,0); lcd.print(" "); lcd.setCursor(0,1); lcd.print(" "); lastTime = micros(); } // ======================== // ======= LOOP ========= // ======================== void loop () { pulse_freq = 1000000.0 / period; lcd.setCursor(0,0); lcd.print("f = "); lcd.print(pulse_freq, 2); lcd.print(" Hz "); lcd.setCursor(0,1); lcd.print(pulse_freq * 60, 0); lcd.print(" RPM "); } // ============================= // ======= INTERRUPT ========= // ============================= void pulse () // Interrupt function { currentTime = micros(); period = currentTime - lastTime; lastTime = currentTime; } |
Auslösen werde ich die Metallkugel mit einem Servo, welcher bequem mittels IR-Fernbedienung angesteuert wird. Die Umsetzung erfolgt ebenfalls mit einem Arduino.

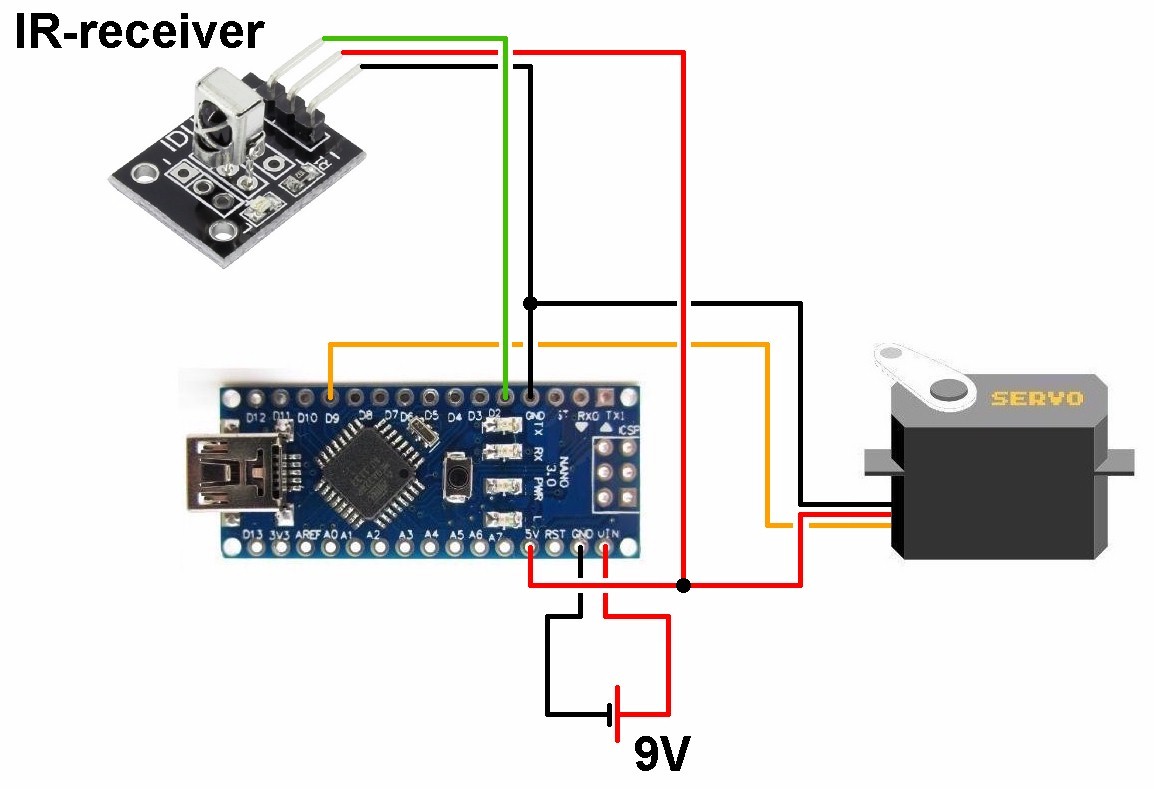







Der Arduino-Code für die Fernbedienung:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
// Written by: Mohamed Soliman // This code is for controlling servo motor with IR remote control // When clicking at any of two buttons the motor is toggling between the rotation and stop #include <IRremote.h> //must copy IRremote library to arduino libraries #include <Servo.h> #define right 0x449E79F //clockwise rotation button #define left 0x8C22657B //counter clockwise rotation button int RECV_PIN = 2; //IR receiver pin Servo servo; int val; //rotation angle bool cwRotation, ccwRotation; //the states of rotation IRrecv irrecv(RECV_PIN); decode_results results; // ================ // === SETUP === // ================ void setup() { Serial.begin(9600); irrecv.enableIRIn(); // Start the receiver servo.attach(9); //servo pin } // =============== // === LOOP === // =============== void loop() { if (irrecv.decode(&results)) { Serial.println(results.value, HEX); irrecv.resume(); // Receive the next value if (results.value == right) { cwRotation = !cwRotation; //toggle the rotation value ccwRotation = false; //no rotation in this direction } if (results.value == left) { ccwRotation = !ccwRotation; //toggle the rotation value cwRotation = false; //no rotation in this direction } } //Serial.print("cwRotation = "); //Serial.println(cwRotation); if (cwRotation && (val != 1)) { val--; //for colockwise button servo.write(val); delay(20); //General speed } if (ccwRotation && (val != 170)) { val++; //for counter colockwise button servo.write(val); delay(20); //General speed } } |
Mehr Informationen zur Fernbedienung gibt es hier: https://stoppi-homemade-physics.de/fernbedienung/
Beim mechanischen Aufbau ging es auch weiter:

Oben in der Leistenmitte erkennt man das 12 mm Loch für die Smartphone-Kamera:


Jetzt fehlt eigentlich nur noch der Isolierrohrbogen EN16, in dem die Kugel dann vom Servo freigegeben wird und auf den Drehteller rollt:
Meine Kinder führten mich als Geburtstagsgeschenk zum Hornbach, wo ich die fehlenden Teile besorgte.



Die 12 mm Metallkugel passt wunderbar durch den Rohrbogen:

Die Position des Rohrbogens wählte ich so, dass durch das Smartphone von oben betrachtet die Kugel das Rohr genau in positiver y-Richtung verlässt. Dies vereinfacht dann enorm die spätere Erfassung der Kugelbahn bzw. deren Startgeschwindigkeit…



Für die Rohrhalterung kam dann auf einer Seite eine längere M4-Gewindestange zum Einsatz, da diese auch gleichzeitig die Plattform für den Servomotor halten sollte:





Der verlängerte Servoarm zum Auslösen der Kugel im Rohrbogen:

So sieht es während des Bastelns auf meinem Küchenboden aus:




Zur Erfassung der Rotationsfrequenz des Drehtellers klebte ich seitlich ein Stück Aluminiumfolie auf:





Der Zusammenschnitt der Ergebnisse bei steigender Drehzahl f:
Ich wollte ja bei diesem Experiment auch die Coriolisbeschleunigung quantitativ erfassen. Dazu lud ich die Videos in der Software Tracker hoch und markierte die Kugelposition Bild für Bild. Zum Kalibrieren musste ich zuvor die Strecke Rohrausgang-Drehtellermitte abmessen:


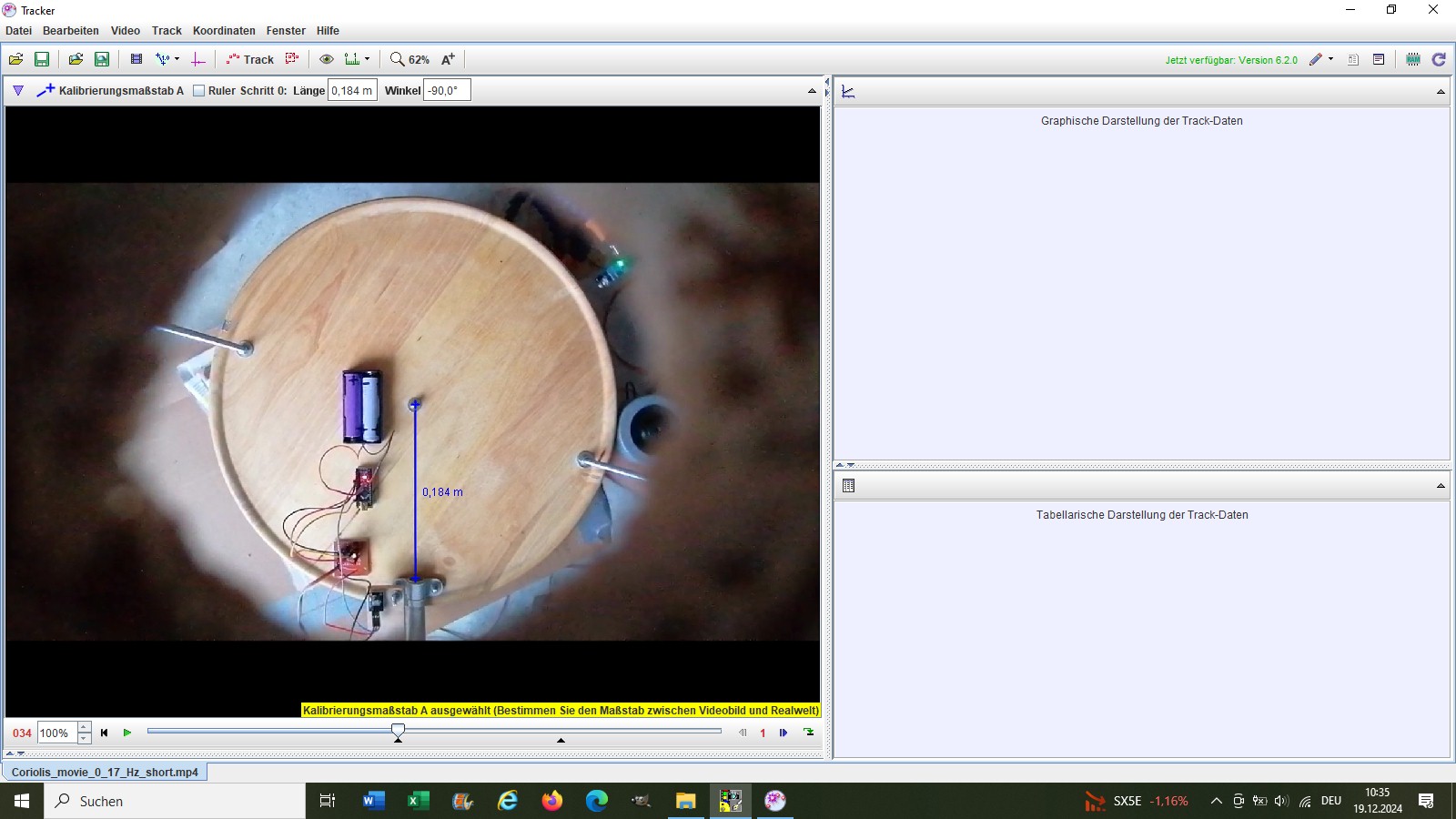
Den Koordinatenursprung legte ich genau in den Ausgang des Rohrs. Wie man sieht ist dieses genau in y-Richtung ausgerichtet. Dies begünstigt die nachfolgende Erfassung der Kugelbewegung gewaltig:

Für die theoretische Bestimmung der Coriolisbeschleunigung a = 2 · v · ω = 2 · v · 2 · π · f benötige ich neben der Drehfrequenz f noch die Startgeschwindigkeit v der Kugel unmittelbar nach Verlassen des Rohrs. Dazu habe ich mir in der Software den Graphen vy(t) ausgeben lassen und die Geschwindigkeit zu Beginn abgelesen. Bei f = 0.19 Hz beträgt zum Beispiel vy = v = 0.671 m/s:
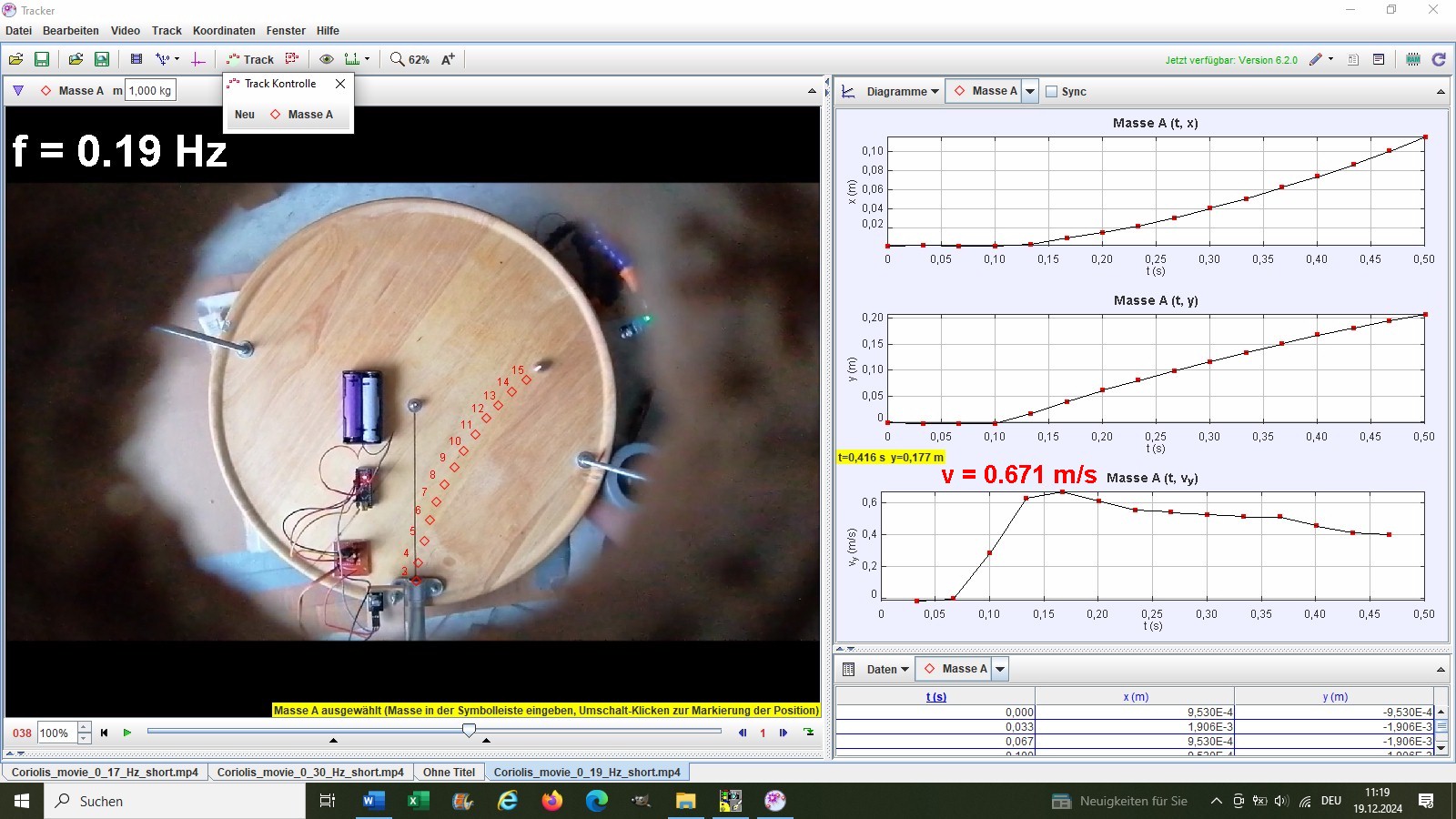
Für die experimentelle Ermittlung der Coriolisbeschleunigung, welche ja kurz nach Verlassen des Rohrs angenähert ausschließlich in x-Richtung wirkt, betrachtete ich den Graphen vx(t). Dessen Steigung entspricht ja dann genau der Coriolisbeschleunigung ac:

So beträgt mein experimentell ermittelter Wert für die Coriolisbeschleunigung bei f = 0.19 Hz ca. ac = 1.50 m/s². Diese Messung wiederholte ich für eine weitere Drehfrequenz f = 0.30 Hz:
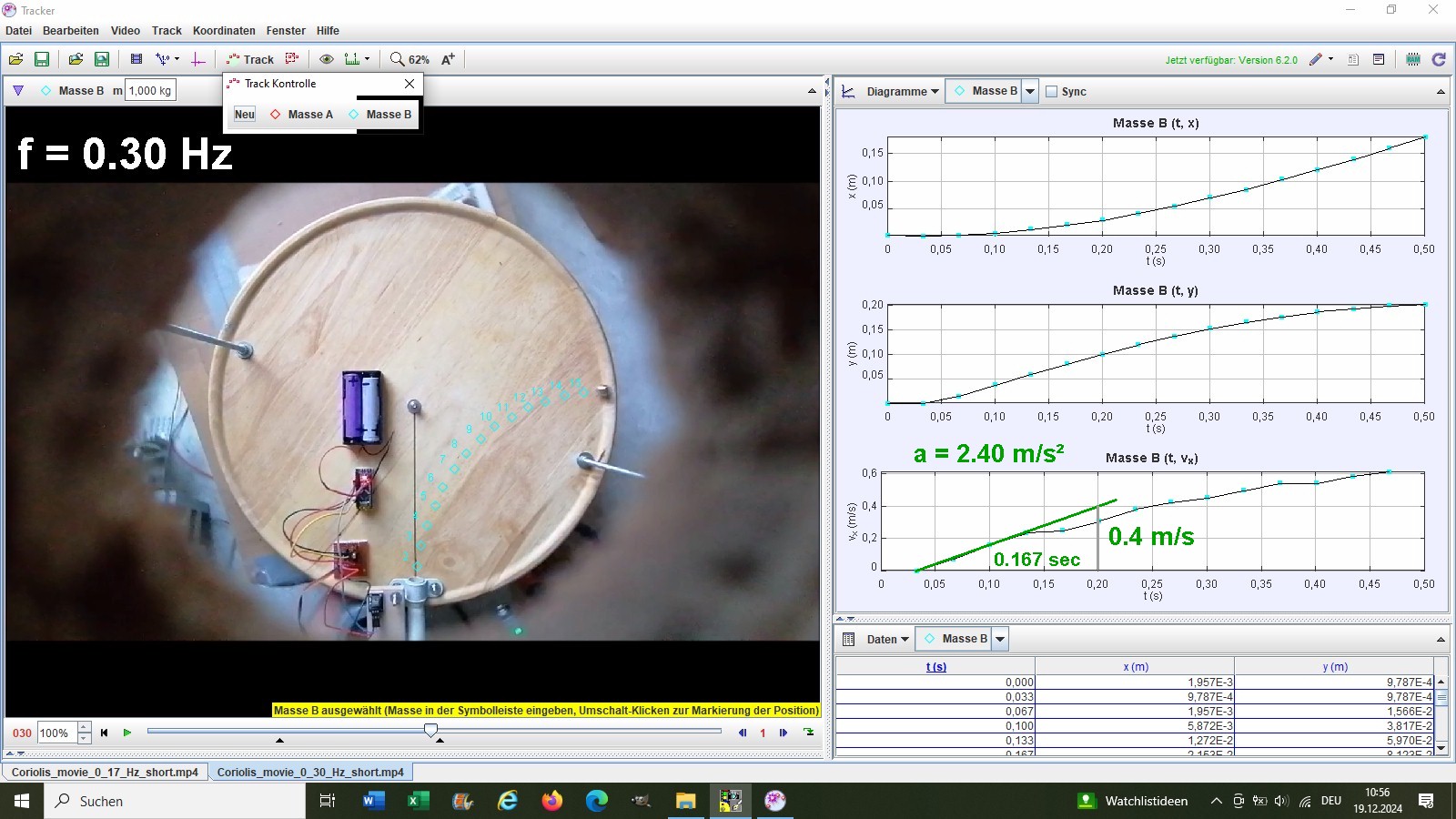
Zum Schluss die Gegenüberstellung von Theorie und Experiment:
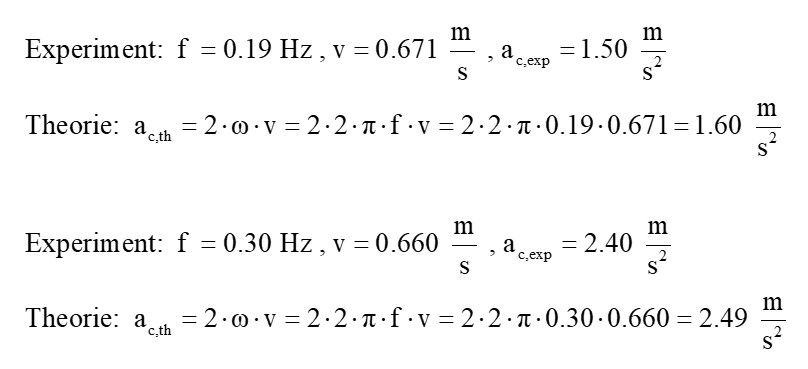
Zu guter letzt habe ich für die Drehfrequenz f = 0.30 Hz die tatsächliche Bahn mit der Simulation verglichen:


Bei einer Simulationsgeschwindigkeit von v = 0.83 m/s erhalte ich eine extrem gute Übereinstimmung zwischen Experiment und Theorie. Die mit der Software Tracker ermittelte tatsächliche/experimentelle Geschwindigkeit der Kugel unmittelbar nach ihrem Austritt aus der Röhre lag etwas tiefer bei ca. 0.7 m/s.
Mit den Ergebnissen bin ich aber insgesamt eigentlich sehr zufrieden. Jetzt muss ich nur noch einen freien Platz in meiner Wohnung zum Aufbewahren des Experiments finden, die wohl mit Abstand schwierigste Aufgabe 😉

