In der Physik sind sog. Erhaltungssätze besonders wichtig, da man diese u.a. für Berechnungen benötigt. Bekannt sind vor allem der Energie- und Impulserhaltungssatz. Mit diesen lassen sich zum Beispiel die Geschwindigkeiten von Kugeln nach einem elastischen Stoß berechnen.

Bei einem elastischen Stoß bleibt die Summe der kinetischen Energien vor und nach dem Stoß konstant. Bei einem inelastischen Stoß bleibt zwar die Gesamtenergie weiterhin konstant, aber die kinetische Energie nimmt nach dem Stoß ab. Die abgenommene Energie steckt dann etwa in Wärme oder Verformungsenergie.
Betrachten wir die elastische Kollision zweier Kugeln mit den Massen m1 und m2 und den Geschwindigkeiten vor dem Stoß v1 und v2:
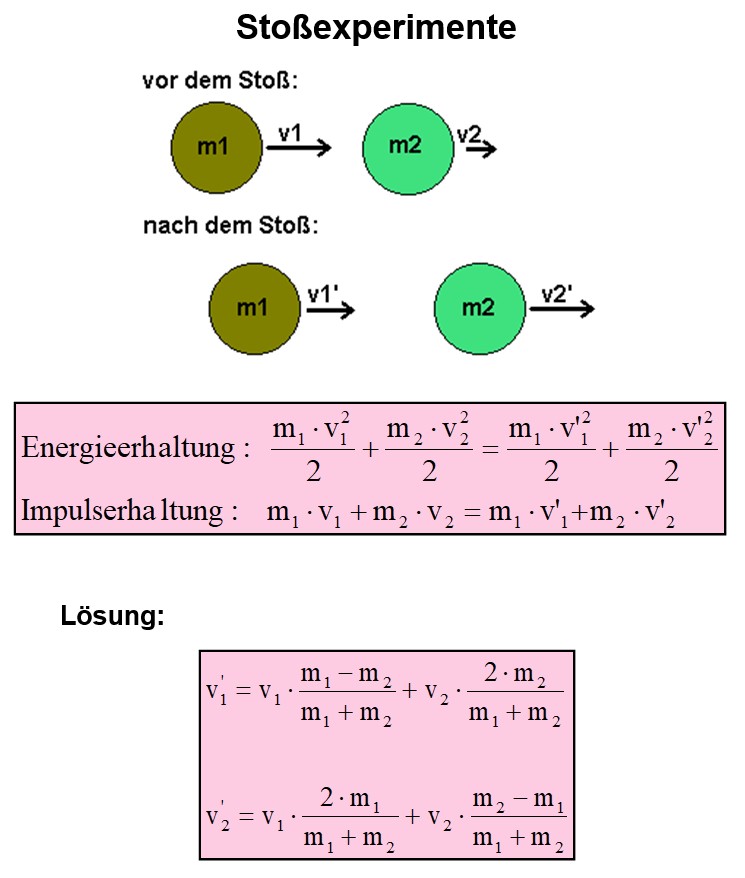
Wir erhalten als Lösung die Geschwindigkeiten v1‚ und v2‚ nach dem Stoß in Abhängigkeit von m1, m2, v1 und v2.
Experiment 1
Zwei gleich schwere Kugeln stoßen zusammen, wobei eine der beiden Kugeln vor dem Stoß ruht.
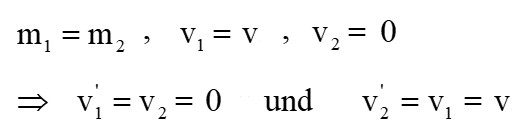
Was bedeutet dieses Ergebnis? Nun, nach dem Stoß ruht die erste Kugel und die zweite Kugel besitzt die Geschwindigkeit der ersten Kugel vor dem Stoß:
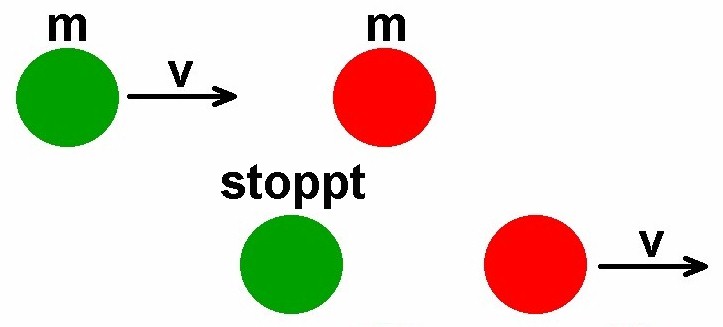
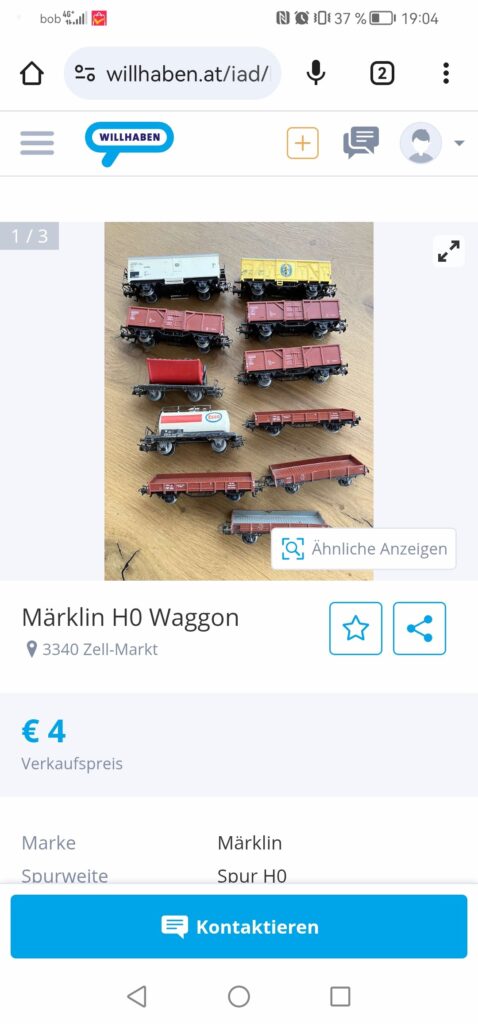
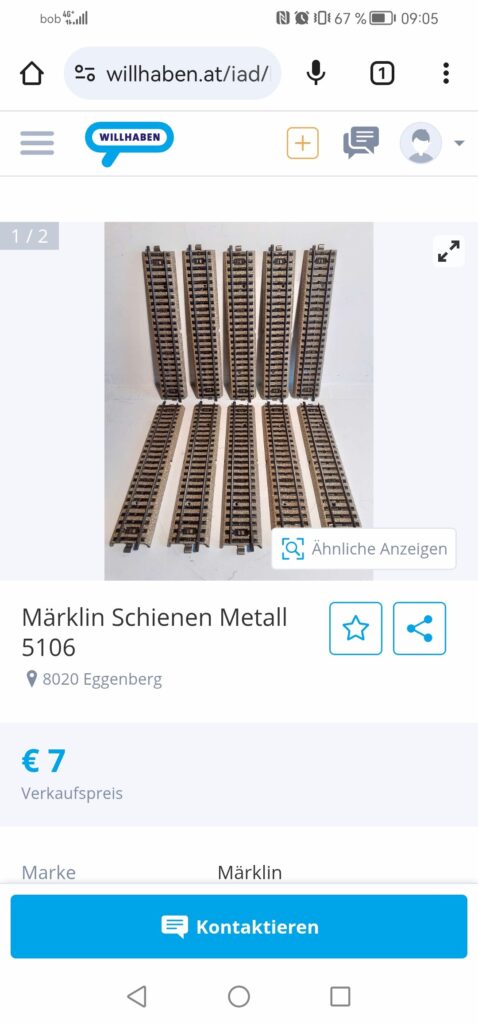
Diese Stoßgesetze lassen sich mit einer Spielzeugeisenbahn überprüfen. Man benötigt hierfür nur zwei Güterwaggons, gerade Schienen und Federblech.





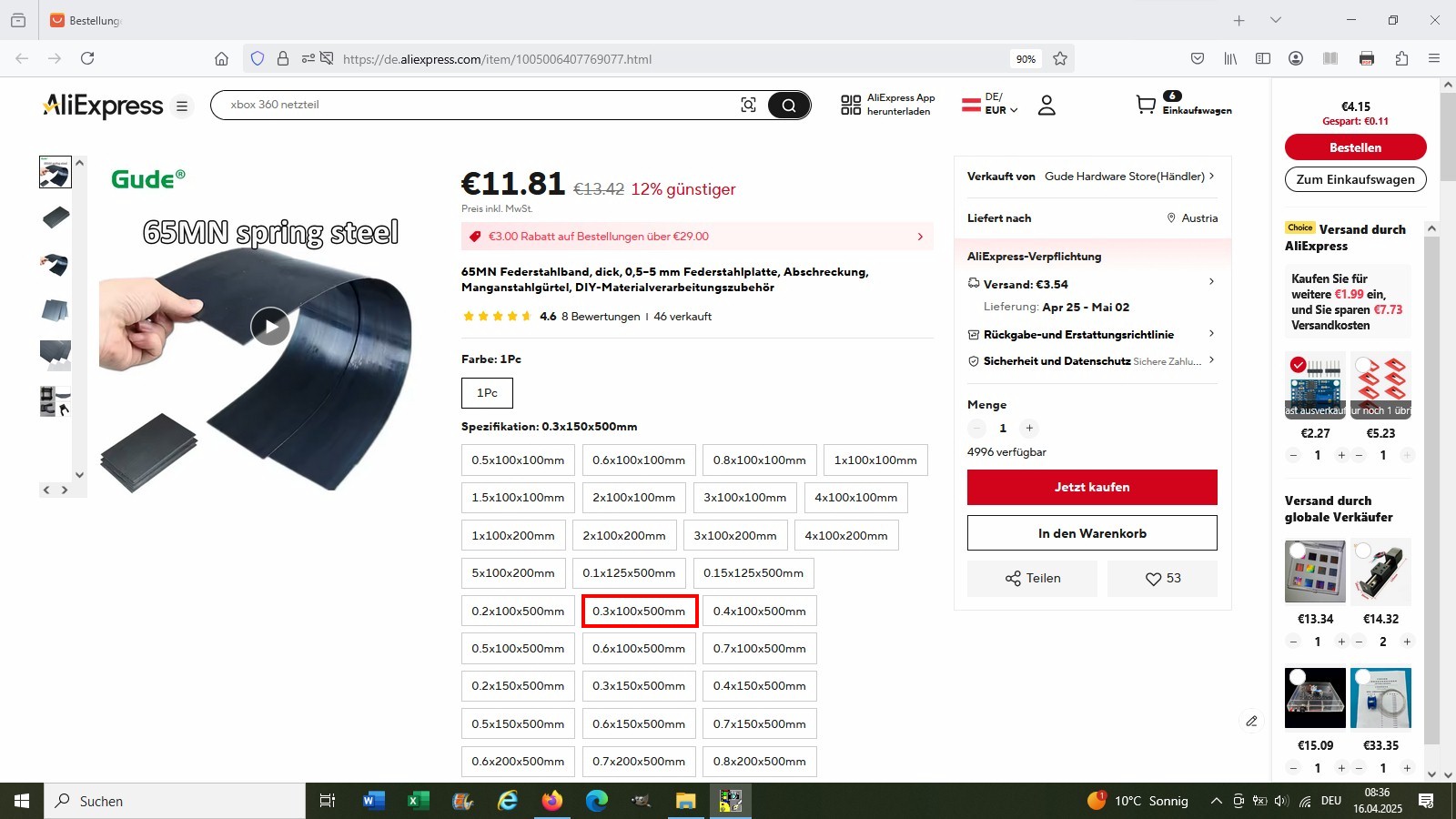
Das Federblech habe ich auf aliexpress gekauft:





Der obige Versuch im Experiment:
Was passiert aber zum Beispiel für den total inelastischen Fall, bei dem die beiden Kugeln nach dem Stoß aneinander kleben bleiben?
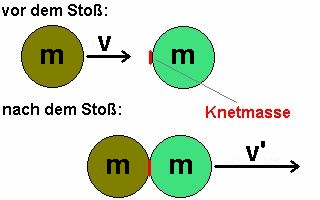
Der Impulserhaltungssatz muss hier weiterhin gelten. Daraus folgt: v‘ = v/2. Berechnet man mit dieser Geschwindigkeit die kinetische Energie nach dem Stoß, so ergibt sich Ekin,nachher = 1/2 · Ekin,vorher. In diesem konkreten Fall verpufft also die Hälfte der kinetischen Energie in Wärme und Verformung!
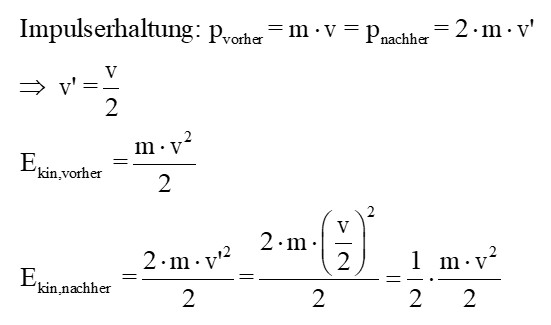
Im ersten Experiment hatten ja die beiden Waggons diesselbe Masse. In weiterer Folge möchte ich aber nun Kollisionen mit unterschiedlichen Massen untersuchen. Dazu verwende ich ein auf Amazon gekauftes Gewichtset:


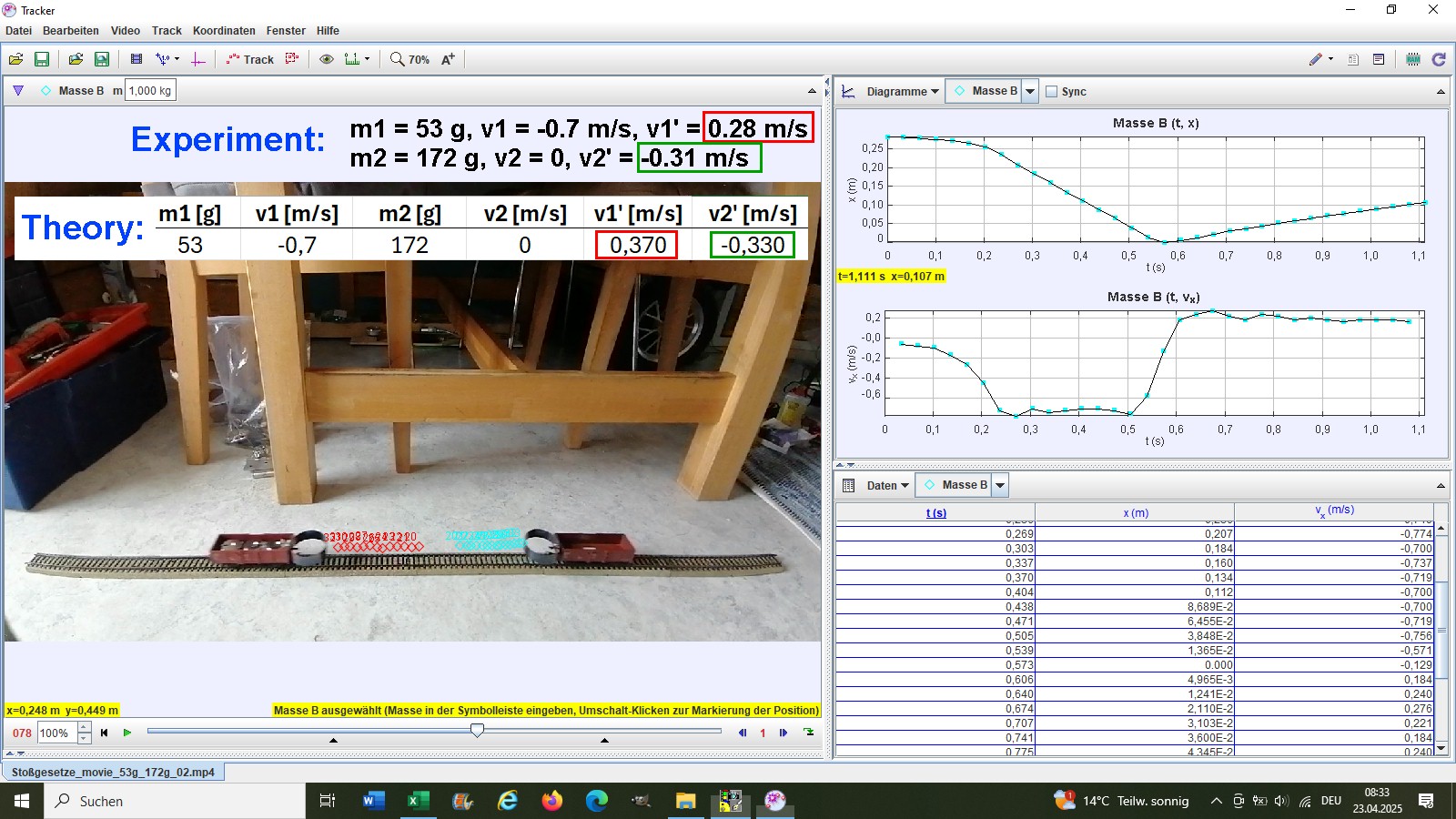
Die experimentelle Auswertung erfolgt per Videoanalyse mit der Software Tracker (https://opensourcephysics.github.io/tracker-website/).
Zum Kalibrieren der Strecke im Video habe ich die Länge der 6 geraden Schienen abgemessen. Ich komme auf eine Gesamtlänge von 107.7 cm, somit beträgt eine Schienenlänge exakt 18 cm.


Experiment 2


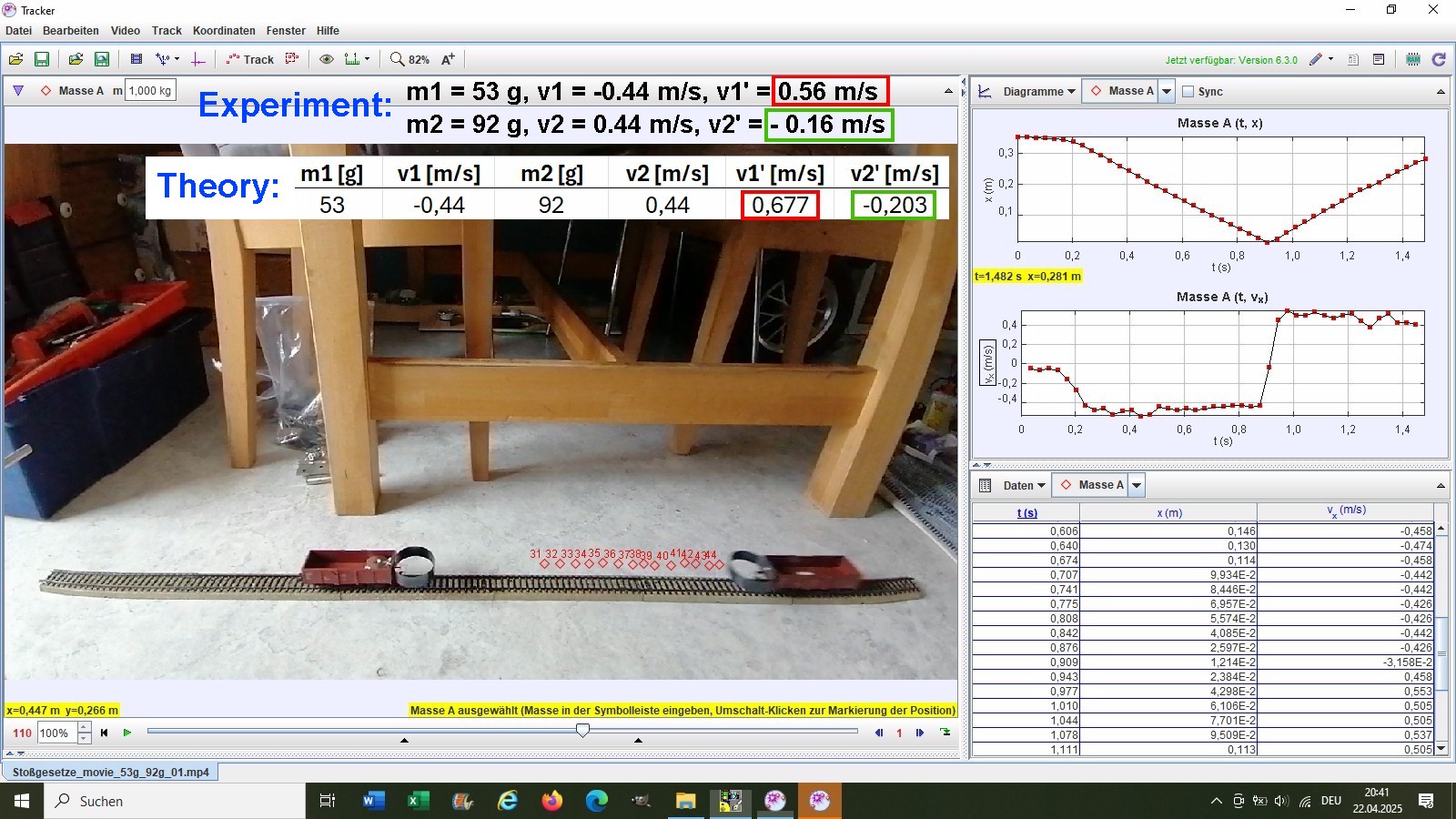

Experiment 3

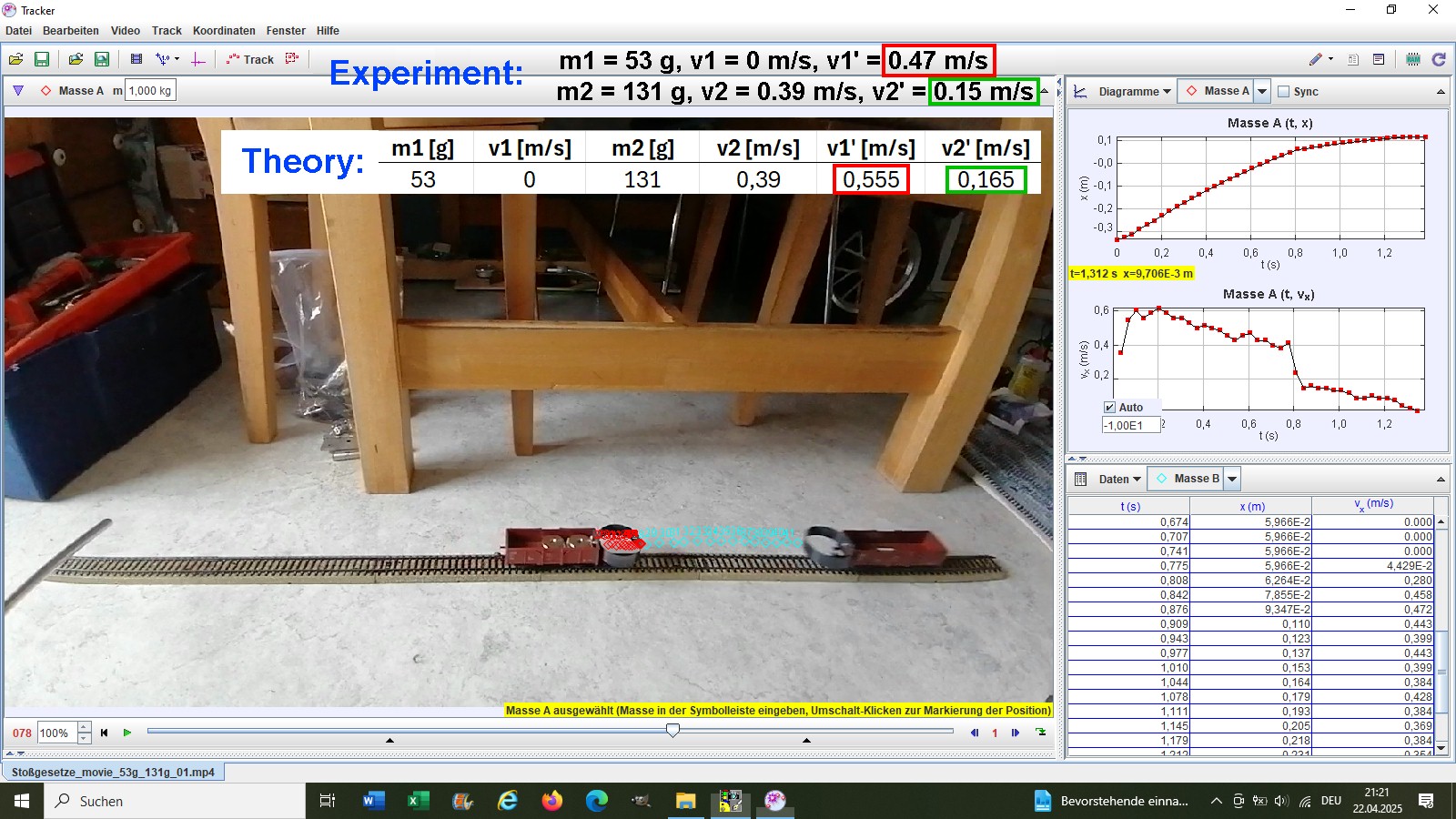
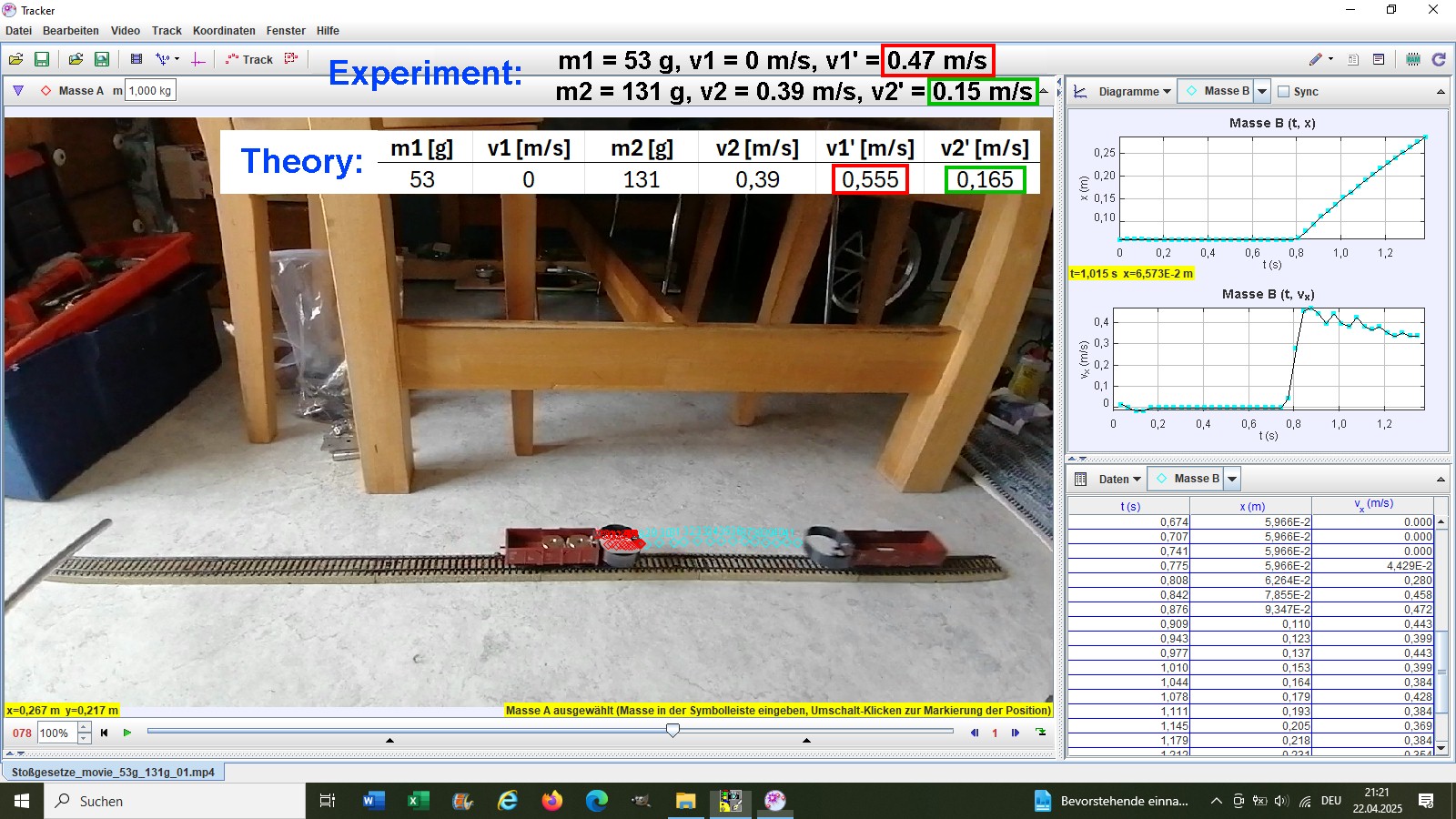
Experiment 4

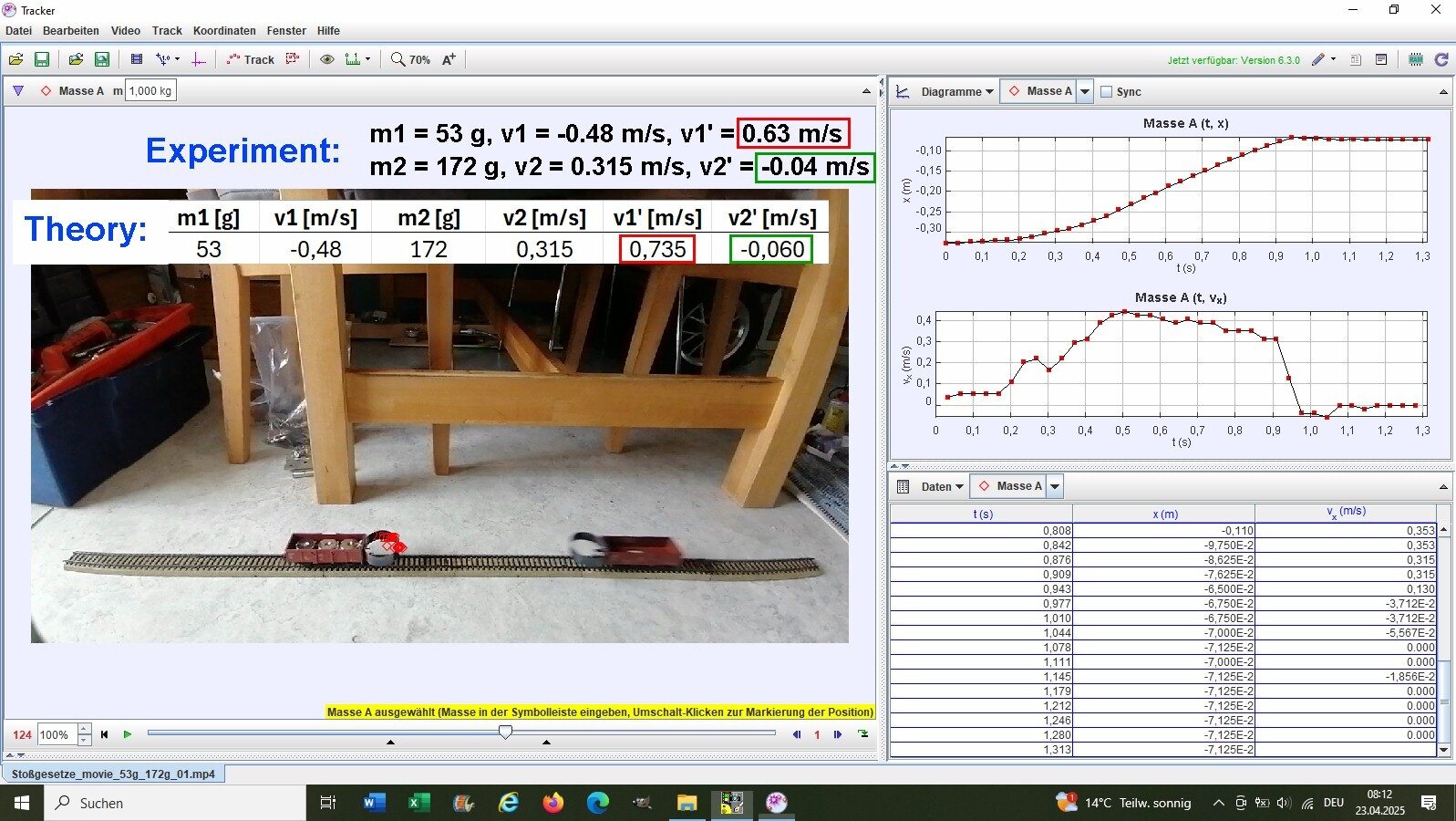
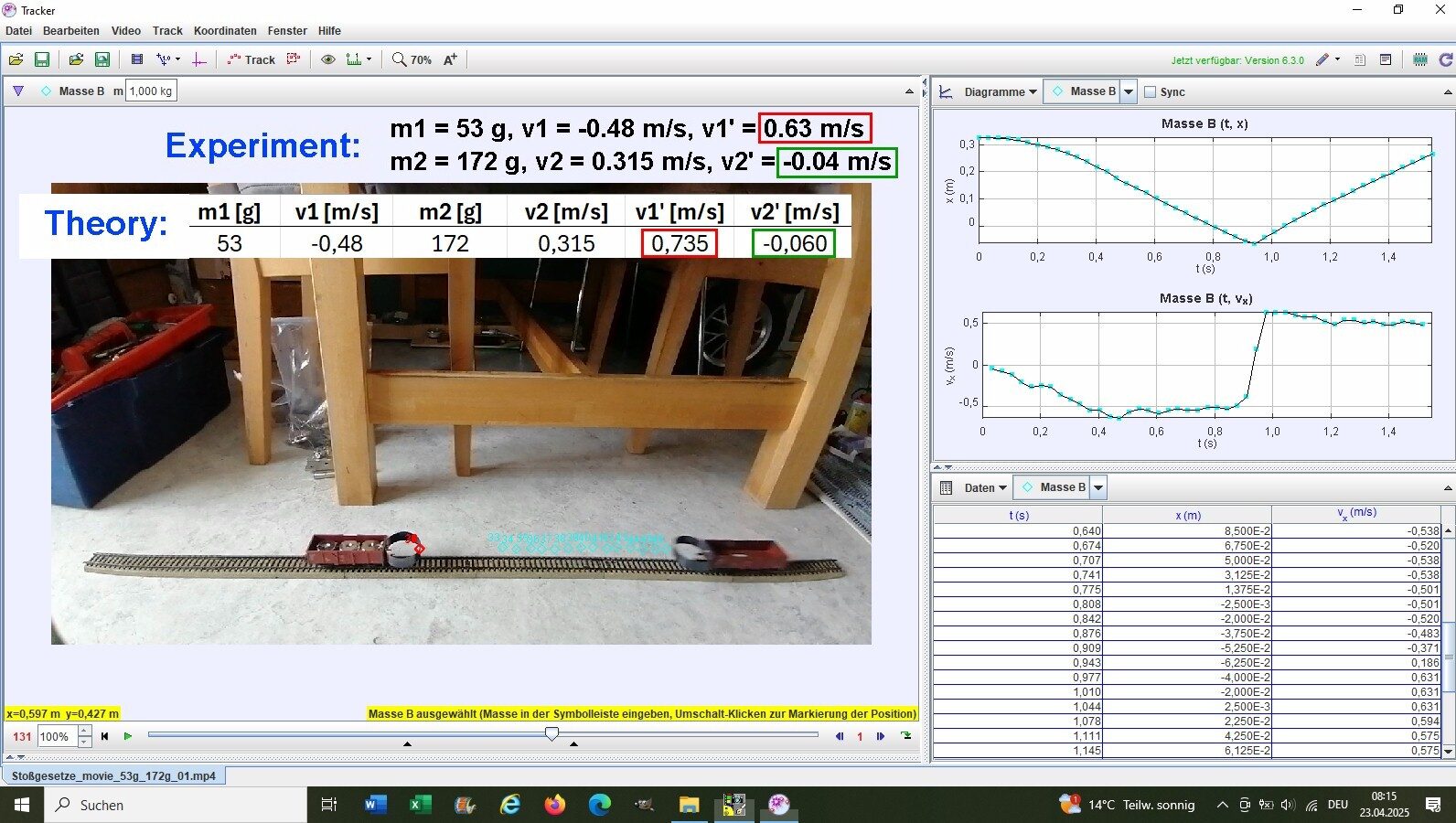
Experiment 5


Experiment 6
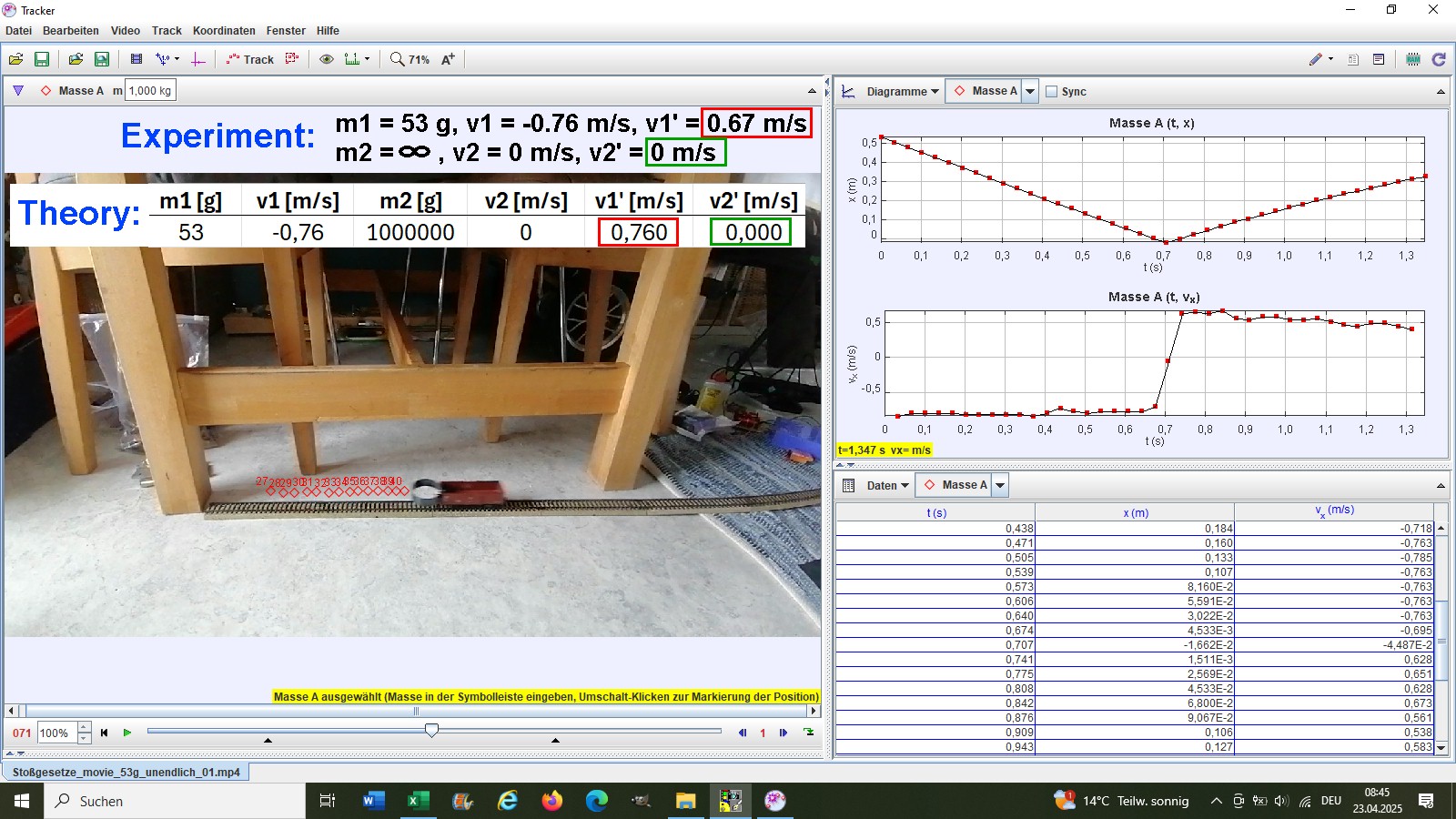
Stößt ein Körper elastisch gegen einen ruhenden, unendlich schweren Körper, so kehrt sich die Geschwindigkeit einfach um. Beispiel: Gummiball fällt auf Erde. Hier habe ich den Waggon mit dem Küchentisch kollidieren lassen.