Wasserschlauchschwingungen
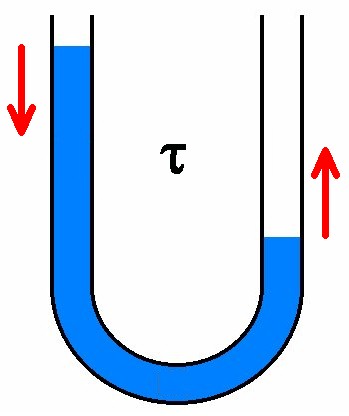
Füllt man einen Schlauch teilweise mit Wasser, formt ein U und saugt dann an einer Öffnung, so versetzt man dadurch das im Schlauch befindliche Wasser in Schwingungen. Von welchen Größen und wie hängt nun die Schwingungsdauer τ ab?
Dazu leiten wir einmal die Beschleunigung a(x) der Wasseroberfläche auf zwei unterschiedliche Arten her:


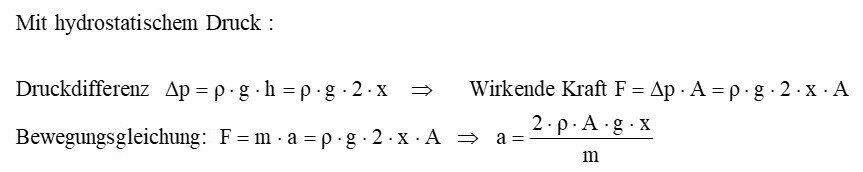
Die Beschleunigung a(x) der Wasseroberfläche hängt also linear von der Auslenkung x ab. Dies erinnert uns aber an das Hook’sche Federgesetz. Daraus schließt man:
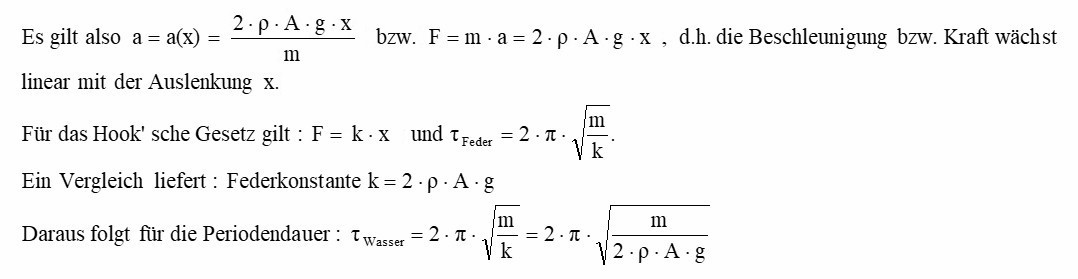
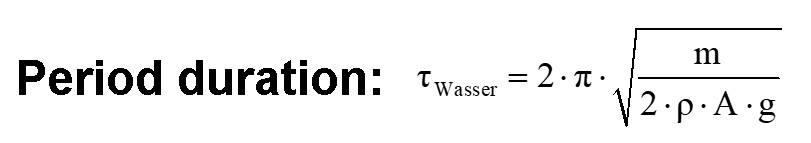
Die Periodendauer τ hängt also von der Wurzel √m der Masse m ab.
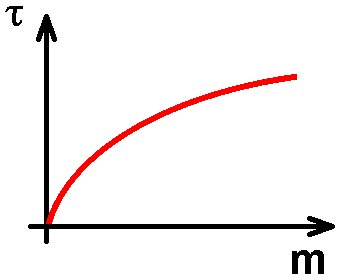
Genau diese Abhängigkeit von m werde ich experimentell überprüfen. Dazu habe ich mir ein U-Rohr-Manometer auf aliexpress gekauft:




Die Durchführung des Experiments erfolgte wie so üblich in meiner kleinen Küche am Boden:

Zur besseren Sichtbarkeit der Wassersäule habe ich dieses mit Lebensmittelfarbe eingefärbt. Für die Bestimmung der Periodendauer verwendete ich die Software „Moviemaker“. Die hat ein Schneidewerkzeug, mit dem man sehr einfach die genaue Zeit an einer bestimmten Videoposition ermitteln kann…
Hier meine Messergebnisse:

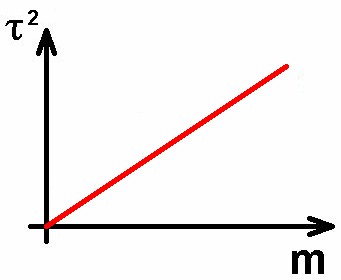
Trägt man das Quadrat der Periodendauer τ² gegen die Wassermasse m auf, so erhalte ich wie erhofft eine ansteigende Gerade. Es gilt also τ² = k · m bzw. τ = k‘ · √m, Heureka…
Die Steigung k meines Graphen τ²(m) beträgt ca. 0.92/8 = 0.115 sek²/g = 115 sek²/kg.
 Laut Theorie müsste für die Steigung aber auch gelten:
Laut Theorie müsste für die Steigung aber auch gelten:


Die Übereinstimmung zwischen Theorie und Experiment ist naja, gerade so akzeptabel 😉
Wasserstrahldose
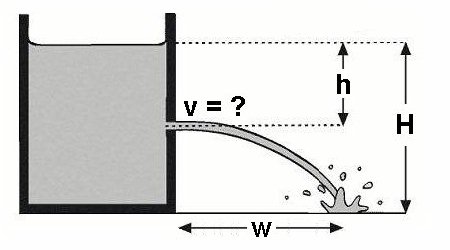
Quelle: Hilscher, H.: Universität Augsburg, Institut für Didaktik der Physik, CD-ROM
Für dieses Experiment benötigt man lediglich eine einseitig verschlossenes Rohr mit mehreren seitlichen Öffnungen. Durch den hydrostatischen Druck schießt das Wasser unterschiedlich schnell aus den Öffnungen heraus. Ziel ist es zunächst die Geschwindigkeit v in Abhängigkeit von der Wassertiefe h zu bestimmen.

Hat man richtig gemessen so erkennt man, dass eine Vervierfachung von h eine Verdopplung der Geschwindigkeit v bewirkt. Es muss also folgender Zusammenhang gelten: v ≡ √h. Wie kann man diese Abhängigkeit herleiten? Wir gehen von der Bernoulligleichung aus:


Diese Formel für v sollte uns an den freien Fall erinnern.

Wir kennen jetzt also die Formel für die Austrittsgeschwindigkeit des Wassers. Befindet sich das Loch weiter oben im Rohr, so ist die Austrittsgeschwindigkeit gering. Das Wasser hat aber in diesem Fall länger Zeit, sich nach rechts zu bewegen, bevor es im Wasserbecken am Boden ankommt. Bei einer Öffnung weiter unten ist es genau anders. Hier ist zwar die Austrittsgeschwindigkeit groß, dafür hat das Wasser nur wenig Zeit, sich nach rechts auszubreiten, bevor es am Boden ankommt. Bei welcher Wassertiefe h kommt nun der Wasserstrahl am weitesten?

Bei einem Loch genau in der Mitte der Wassersäule kommt also der austretende Wasserstrahl am weitesten.
Für das Experiment habe ich mir ebenfalls auf aliexpress ein Plexiglasrohr und Schlauchtüllen mit Gewinde aus Messing besorgt. Eine passende Wasserpumpe hatte ich noch in meiner Bastelkiste…
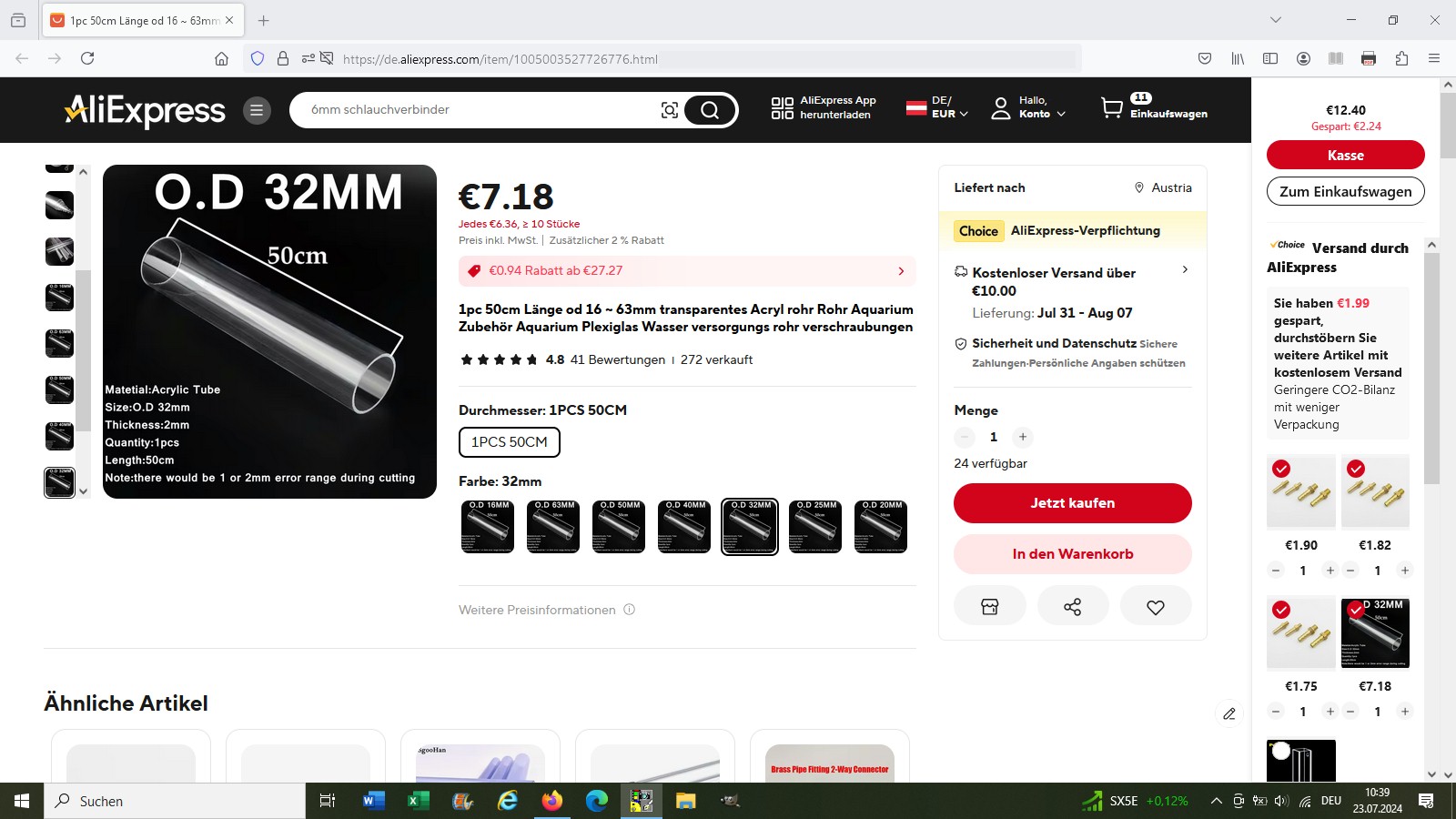

Hier der schematische Versuchsaufbau:
Die Teile sind mittlerweile bei mir angekommen:









Damit meine Küche während des Experiments nicht total absäuft, habe ich mir eine lange Blumenkiste besorgt:

Hier die verwendete Pumpe, welche von ihrer Pumpleistung ideal für dieses Experiment passt:




Zuerst habe ich immer nur ein einzelnes Loch geöffnet und die Spritzweite w ermittelt. Die Gesamthöhe der Wassersäule bis zur Wasseroberfläche im Kisterl betrug H = 48 cm. Im Folgenden die Ergebnisse für unterschiedliche Höhen/Tiefen h:
h = 8 cm:

h = 16 cm:

h = 24 cm:

h = 32 cm:

h = 40 cm:

Aus w, h und H konnte ich dann die Ausströmgeschwindigkeit v ermitteln:
Ich erhalte zwar einen Zusammenhang v² ≡ h bzw. v ≡ √h, allerdings weichen meine experimentellen Ergebnisse doch merklich von den theoretischen Sollwerten v = √2·g·h ab. Den Grund dafür kenne ich im Moment noch nicht…
Im zweiten Teil des Experiments ging es um die maximale Spritzweite w. Diese sollte ja bei h = H/2 vorliegen. Dazu habe ich sämtliche Löcher geöffnet. Wie wir schon beim ersten Experiment vorhin gesehen haben, spritzte das Wasser bei h = 24 cm = H/2 am weitesten, Heureka 😉

Das Youtube-Video:
Wasserwellenmaschine
Für dieses Experiment benötigt man eine durchsichtige Flasche, Lebensmittelfarbe und Babyöl. Ich habe mein Plastikgefäß auf Temu für nur 5 Euro bestellt:


Das Babyöl stammt von Bipa:

Das Plastikgefäß muss natürlich komplett verschlossen werden. Zum Glück hatte ich noch eine passende Plexiglasplatte und Plexiglaskleber zuhause:



Die fertige Box:

Zum Einfüllen des gefärbten Wassers und des Babyöls benötigt man eine kleine Öffnung, vorzugsweise in einer Ecke. Hier kam mir der kleine Transportschaden sogar sehr gelegen 😉

Die blaue Lebensmittelfarbe zum Färben des Wassers:


Eine Spritze eignet sich zum Einfüllen der Flüssigkeiten:
Zuerst kommt das gefärbte Wasser in das Plastikgefäß…

…und danach das Babyöl:


Die kleine Öffnung in der Ecke habe ich dann mit 2-Komponentenkleber wieder verschlossen:

Die fertige Wellenmaschine:

Kippt man nun den Behälter abwechselnd nach links und rechts, so entstehen sehr schöne Wellenmuster:



Diese Kippbewegung kann man manuell ausführen oder man baut sich mit einem Getriebemotor einen Kippmechanismus.
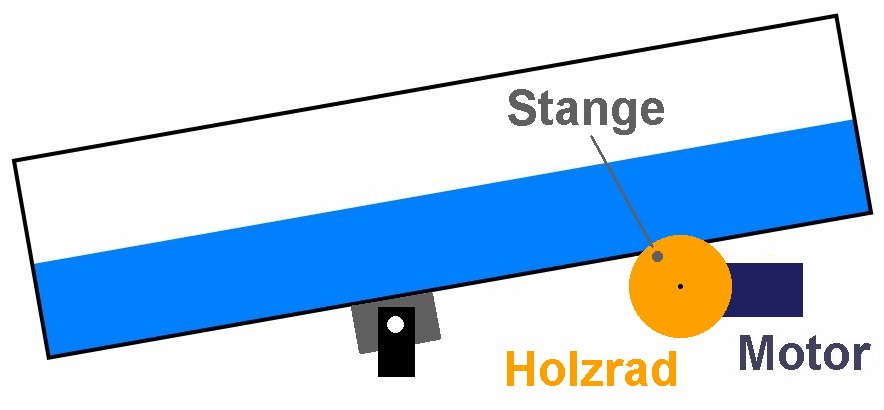
Den Motor mit 10 rpm habe ich auf Amazon bestellt:



Bei den Holzteilen greife ich sehr gerne auf Teile der österreichischen Firma Matador (https://www.matador.at/) zurück:



Beim Basteln sieht meine Küche zwischenzeitlich eher wie eine Werkstatt aus 😉







Leider beschlägt sich die Innenseite des Plexiglases durch das Babyöl ein wenig und erscheint trüb. Daher habe ich mir auf http://www.willhaben.at Silikonöl gekauft in der Hoffnung, dass dann alles schön klar bleibt. Mal schauen, ob dieser Plan aufgeht…
Das Silikonöl mit einer Zähigkeit/Viskosität von 300 cSt ist angekommen. Es ist allerdings viel zu zähflüssig und es bilden sich dadurch keine schönen Wellenmuster aus:

Also nochmals zwei Flaschen Babyöl von Amazon und Plastikboxen von Temu besorgt und einen weiteren Versuch gestartet.

Nun bin ich mit den Ergebnissen zufrieden. Bei 12V Spannung dreht sich der Getriebemotor auch ausreichend schnell und es entstehen einigermaßen spannende Wellenmuster.




Schweres Wasser
Wie viele wissen besitzt Wasser eine Dichte von fast genau 1 g/cm³. Aber es gibt tatsächlich auch schwereres Wasser. Dessen Dichte wollen wir in diesem kurzen Versuch bestimmen. Dazu benötigen wir ein Pyknometer und eine Feinwaage.


Zuerst wiegen wir das Pyknometer ohne Inhalt:

Die Waage zeigt 13.000 g an. Danach füllen wir das Pyknometer mit ganz gewöhnlichen Wasser. Nun zeigt die Waage 18.509 g an. Gehen wir von einer Wasserdichte von genau 1.0 g/cm³ aus, so muss das Wasser- bzw. Pyknometervolumen V = m / ρ = 5.509 / 1 = 5.509 cm³ betragen:

Komischerweise ist das Pyknometer mit 5 ml = 5 cm³ beschriftet. Pyknometer werden ja zur Bestimmung der Dichte von Flüssigkeiten verwendet und besitzen daher eigentlich ein sehr genau angegebenes Volumen. Warum hier eine Abweichung von rund 10% besteht ist mir ehrlich gesagt schleierhaft.
Jetzt kommt das „Zauberwasser“ zum Einsatz. Wieder wird das Pyknometer mit dem nun bekannten Volumen V gefüllt und gewogen:

Die Waage zeigt nun mehr an, konkret 19.087 g. Die Dichte dieses Wassers muss also deutlich über 1 g/cm³ liegen. Die kurze Rechnung:

Die Dichte des schweren Wassers beträgt also 1.1049 g/cm³. Wie kann dies sein?
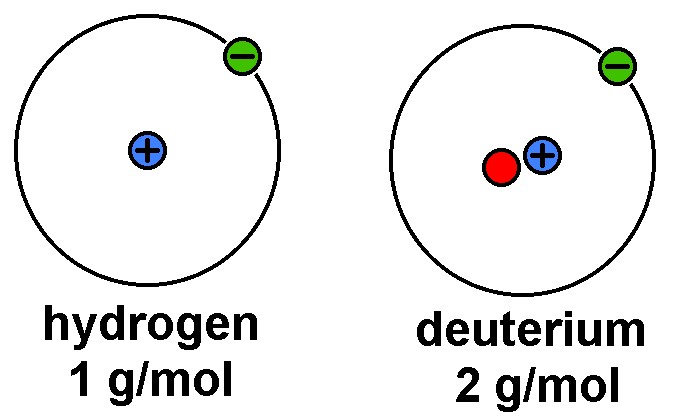

Gewöhnliches Wasser besteht ja aus zwei Wasserstoffatomen und einem Sauerstoffatom. Wasserstoff besitzt jedoch 2 Isotope mit gleicher Kernladungszahl (Anzahl der Protonen) aber unterschiedlicher Massenzahl (Anzahl der Protonen + Neutronen) und zwar Deuterium (1 Proton + 1 Neutron) bzw. Tritium (1 Proton + 2 Neutronen). Schweres Wasser hat die Summenformel D2O, besteht also aus 2 Deuteriumatomen und 1 Sauerstoffatom. Normaler Wasserstoff wiegt pro Mol 1 g, Deuterium aber durch das zusätzliche Neutron 2 g. Gewöhnliches Wasser hat eine Molmasse von 18 g (Sauerstoff 16 g, zwei Mal Wasserstoff mit je 1 g), schweres Wasser hingegen 20 g (Sauerstoff 16 g plus 4 g für die beiden Deuteriumatome). Wenn nun gewöhnliches Wasser eine Dichte von 1 g/cm³ besitzt, müsste schweres Wasser eine Dichte von 1 · 20 / 18 = 1.111 g/cm³ aufweisen, wenn die Anzahl der Moleküle pro cm³ bei Wasser und schwerem Wasser gleich bleibt. Die experimentell ermittelte Dichte von 1.1049 g/cm³ liegt nicht weit vom Sollwert entfernt.
Schweres Wasser besitzt also eine um rund 10% höhere Dichte als gewöhnliches Wasser. Zum Einsatz kommt es etwa bei Schwerwasserkernreaktoren, denn schweres Wasser absorbiert deutlich weniger Neutronen als normales Wasser. Dadurch muss der Kernbrennstoff bei Schwerwasserreaktoren weniger/gar nicht angereichert sein.

Das für dieses Experiment verwendete Deuteriumoxid habe ich dankenswerterweise geschenkt bekommen. Die Preise für D2O sind sehr hoch und man zahlt schnell über 2000 Euro pro Liter!

