Für diesen netten Versuch benötigt man ein einfaches Holzhaus mit/ohne Dämmung, eine Halogenlampe (in meinem Fall ein 12V/50W Modell) und ein Thermometer.
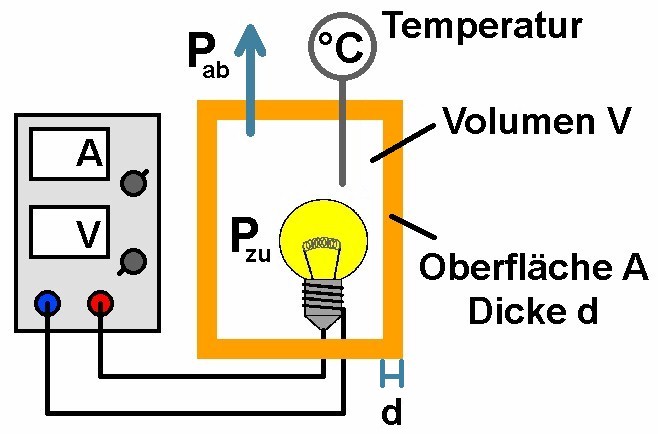
Die benötigte Formel für die Bestimmung der Wärmeleitfähigkeit λ der Holzwände lautet:
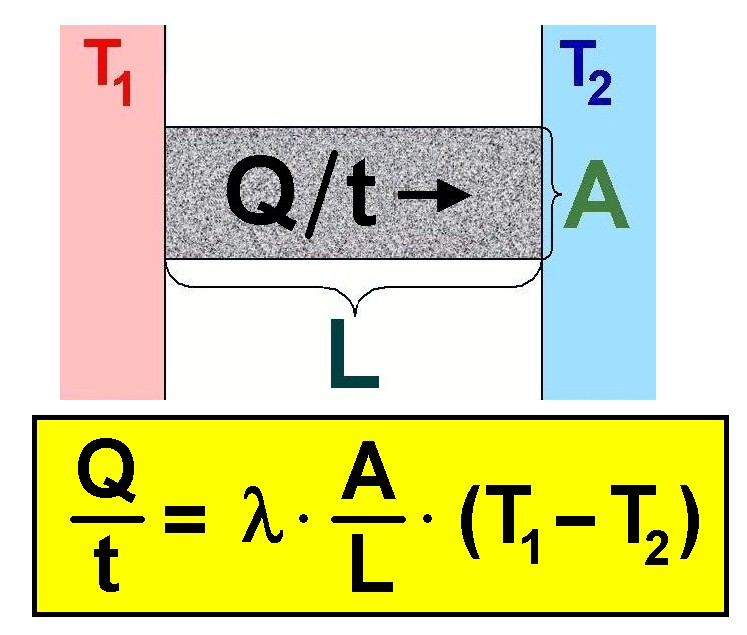
Der Wärmestrom Q/t ist bei gegebener Länge L, Fläche A und Temperaturunterschied T1 – T2 proportional zur Wärmeleitfähigkeit λ. Je größer λ, desto besser leitet der Stoff die Wärme. Metalle besitzen etwa eine hohe Wärmeleitfähigkeit, Isolatoren eine niedrige.
Basis meines Holzhauses war eine 7 mm starke Holzplatte aus dem Baumarkt:

Gesägt wird obligatorisch am Küchentisch 😉


Hier die verwendete Halogenlampe:





Die Plattendicke beträgt wie schon erwähnt 7 mm…

und die Fläche einer einzelnen Wand rund 100 cm²:

Schaltet man die Halogenlampe (Spannung U, Stromstärke I, Leistung P = U·I = Q/t) ein, so steigt zunächst die Innentemperatur schnell an um sich dann einem Endwert Tinnen zu nähern. Daraus lässt sich dann die Wärmeleitfähigkeit λ berechnen:
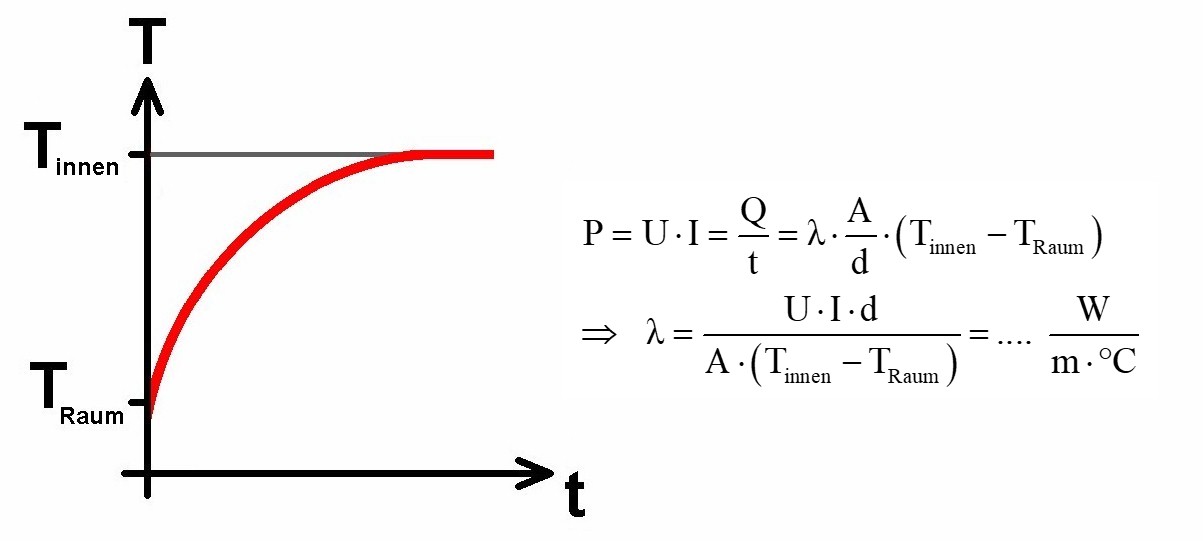
In meinem Fall betrug diese Endtemperatur ca. 85°C:

Der erhaltene Kurvenverlauf der Funktion T(t):
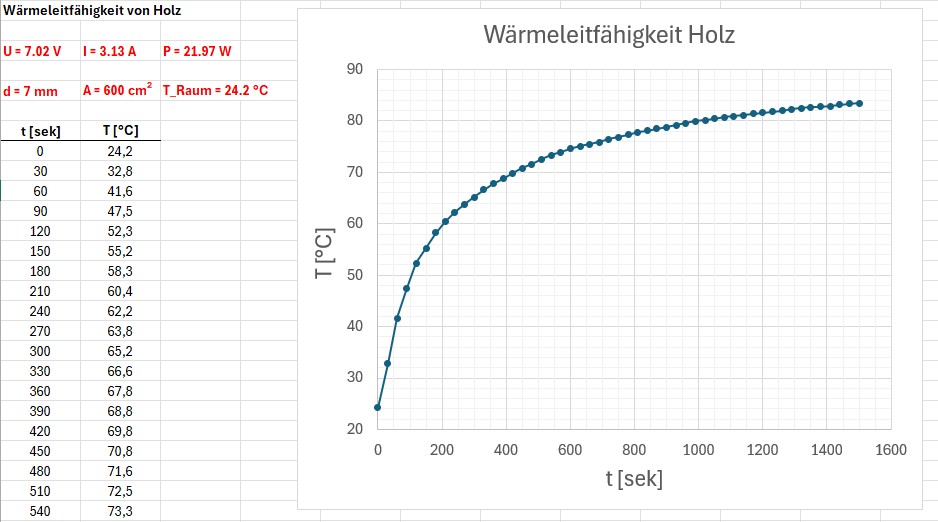
Setzt man die Werte in die obige Formel ein, so erhalte ich

Ein Recherche im Internet ergab, dass dieser Wert für λ durchaus realistisch ist:
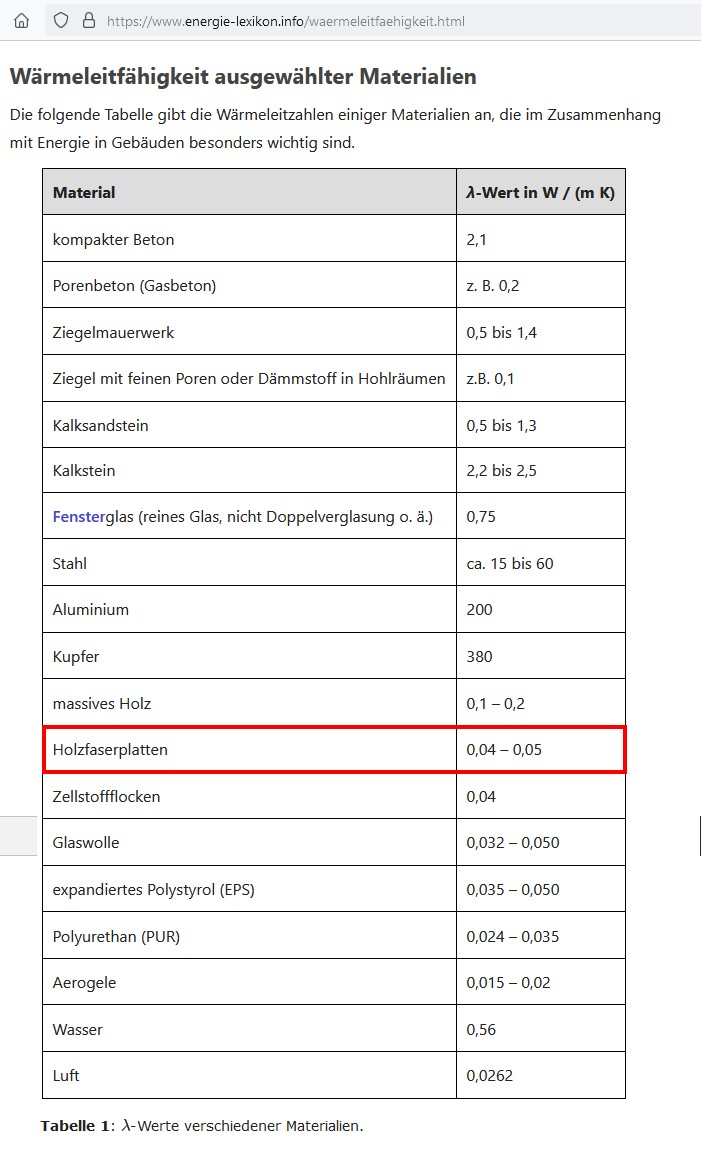
Quelle: https://www.energie-lexikon.info/waermeleitfaehigkeit.html
Kleine Anmerkung: In die Formel für den Wärmestrom Q/t habe ich die Temperaturdifferent Tinnen – TRaum eingesetzt. Dies ist nicht ganz korrekt, denn auf der Aussenseite der Holzwände betrug die Temperatur mit Sicherheit mehr als die Raumtemperatur. Für die dann geringere Temperaturdifferenz Tinnen – TAussenseite erhält man eine größere Wärmeleitfähigkeit λ.
Den Versuch habe ich auch dazu verwendet, die spezifische Wärmekapazität von Luft zu bestimmen. Führt man einem Stoff der Masse m eine Wärmemenge Q zu, so steigt dessen Temperatur um ΔT:
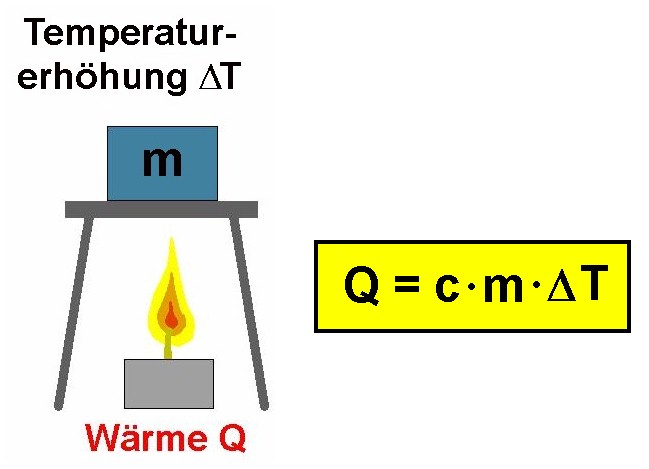
c ist die spezifische Wärmekapazität des Stoffes und diese entspricht der benötigten Wärme, um 1 kg um 1°C zu erwärmen. Ein leicht zu erwärmender Körper besitzt demnach eine geringe spezifische Wärmekapazität und vice versa.
Betrachten wir noch einmal den Temperaturverlauf T(t). Zu Beginn erwärmt die Halogenlampe weitestgehend nur die im Inneren befindliche Luft. Aus dem Temperaturanstieg ΔT/Δt bzw. dT/dt kann man dann die spezifische Wärmekapazität ermitteln:
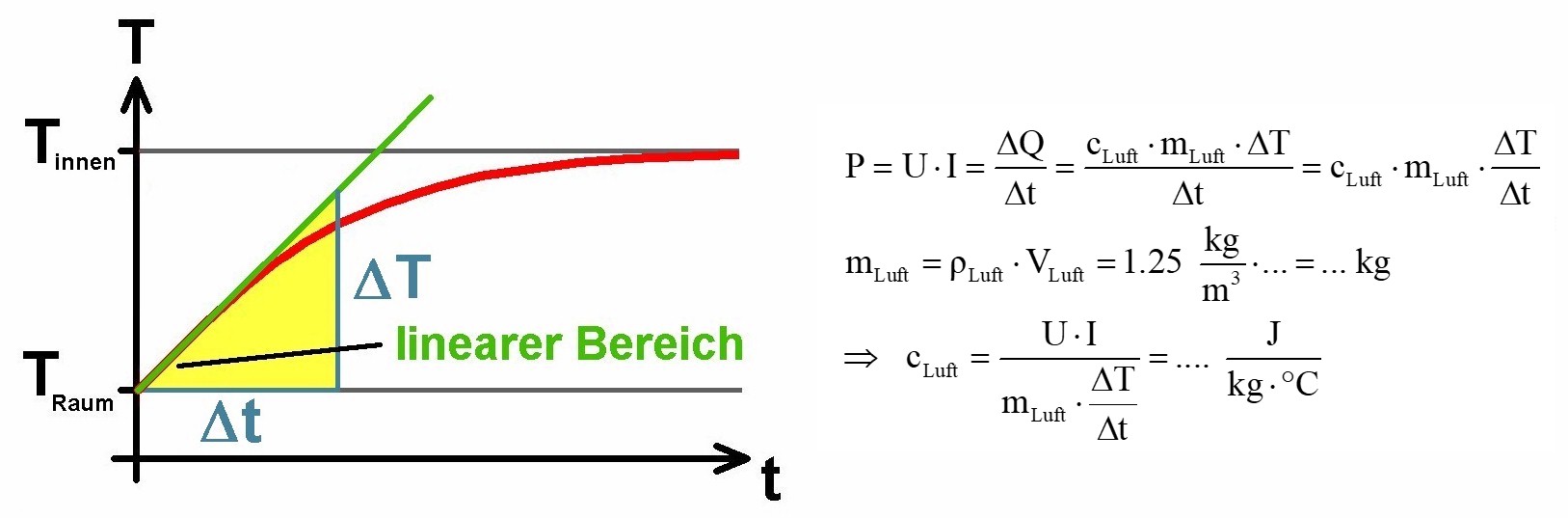
Hier der in einem zweiten Versuch erhaltene Graph T(t) für die ersten Sekunden:
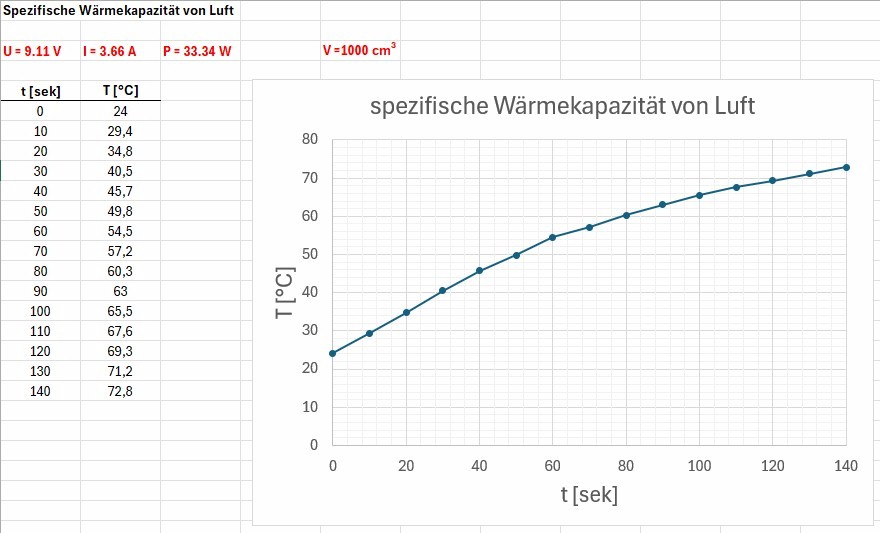
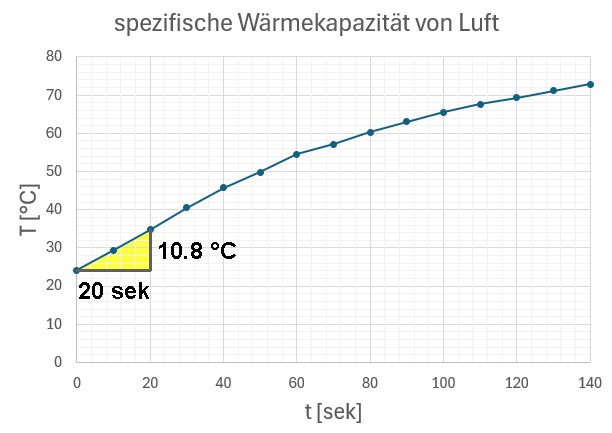 Die Rechnung zur Bestimmung von cLuft:
Die Rechnung zur Bestimmung von cLuft:
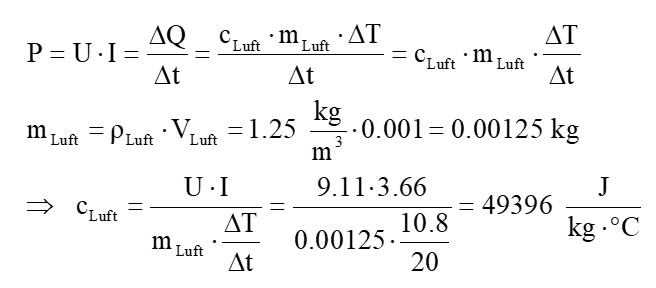
Leider liege ich mit meinem Wert von fast 50 kJ/kg·°C um den Faktor 50 (!) vom Sollwert (rund 1 kJ/kg·°C) entfernt. Die durch die Lampe abgegebene Leistung wird also bei weitem nicht nur für die Erwärmung der Luft investiert sondern in einem viel stärkeren Maße für die Erwärmung des Holzes usw. Überrascht hat mich das Ergebnis aber dennoch…

