Führt man Wasser eine bestimmte Energie/Wärme zu, so steigt seine Temperatur. Pro Grad Celsius und pro Kilogramm Wasser benötigt man eine Energie von rund 4.19 kJ. Dieser Wert entspricht der spezifischen Wärmekapazität von Wasser.

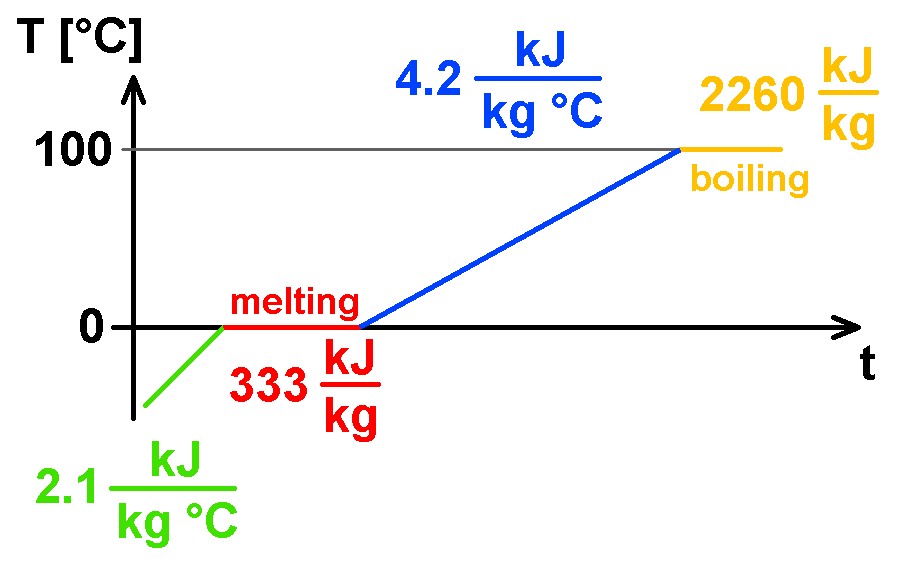
Für Eis benötigt man etwas weniger Wärme zum Erhitzen, nämlich 2.1 kJ/kg·°C. Schmilzt das Eis dann bei 0°C, so steigt trotz Wärmezufuhr die Temperatur nicht an. Die Energie/Wärme wird dann also nicht für eine Temperaturerhöhung benötigt, sondern für den Phasenübergang fest-flüssig. Zum Schmelzen von 1 kg Eis benötigt man die beachtliche Wärmeenergie von 333 kJ. Für die Masse m_ice bedarf es dann logischerweise der Energie Q = 333 kJ · m_ice = c_melt · m_ice. Die Schmelzwärme c_melt von Eis möchte ich im nachfolgenden Experiment wiefolgt ermitteln.

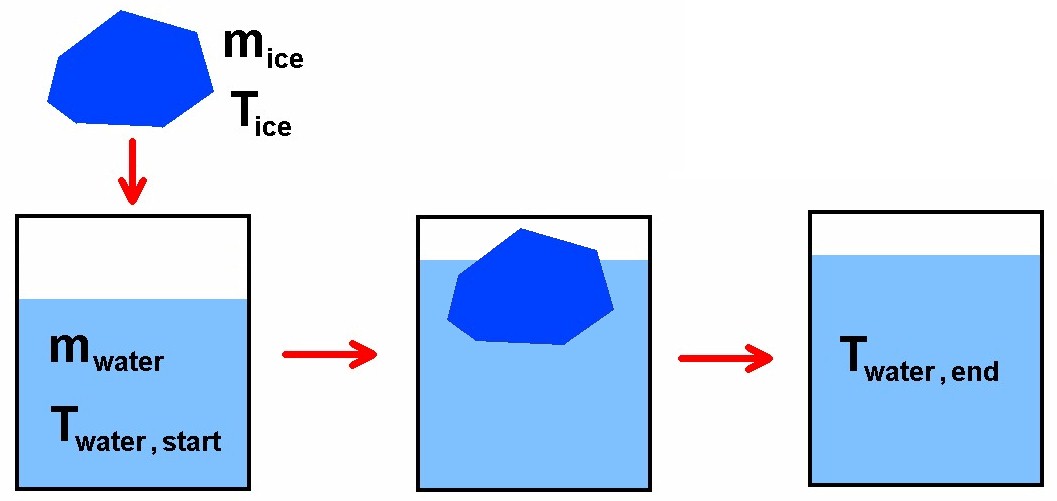
Ein Eiswürfel der Masse m_ice  und der Temperatur T_ice  wird in heißes Wasser der Masse m_water und der Tempertur T_{water, start} gegeben. Der Eiswürfel löst sich auf und kühlt das Wasser auf eine Endtemperatur T_{water, end} ab. Aus diesen Werten lässt sich dann die Schmelzwärme c_melt von Eis/Wasser berechnen.

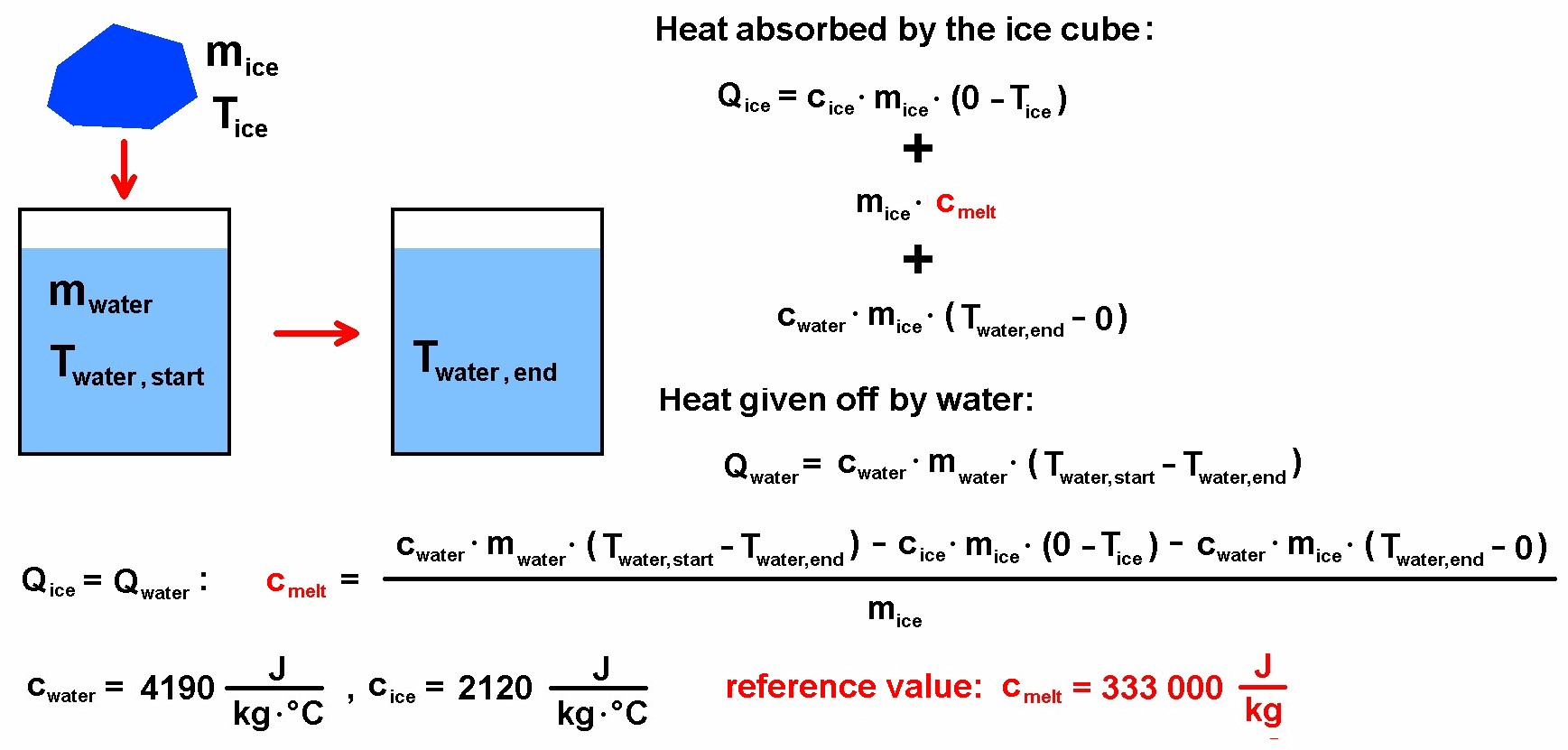
Der gesamte Versuchsaufbau:

Das Thermometer zur Bestimmung der Temperatur des Eiswürfels:

Das Thermometer für die Bestimmung der Wassertemperatur:

Die Waage zur Ermittlung der Masse des Eiswürfels bzw. des heißen Wassers:

Der Eiswürfel noch im Glas:

Der Messbecher für das heiße Wasser:

Der Wasserkocher zum Erhitzen des Wassers:

Die Temperatur des Eiswürfels betrug – 6.5°C:

Die Masse des Eiswürfels wurde zu m_ice = 145 g bestimmt:

Das heiße Wasser wog m_water = 467 g…

…und besaß vor dem Hinzugeben des Eiswürfels eine Temperatur von T_{water, start} = 87.1 °C:

Hier die Temperatur während der Abkühlung des Wassers durch den Eiswürfel:

Als sich der Eiswürfel komplett aufgelöst hat, besaß das Wasser eine Temperatur von nur noch T_{water, end} = 46.1 °C:

Hier das Versuchsprotokoll auf einem Schmierzettel 😉

Setzt man diese Werte in die obige Formel ein, so erhält man folgendes Resultat für die Schmelzwärme c_melt von Eis/Wasser:

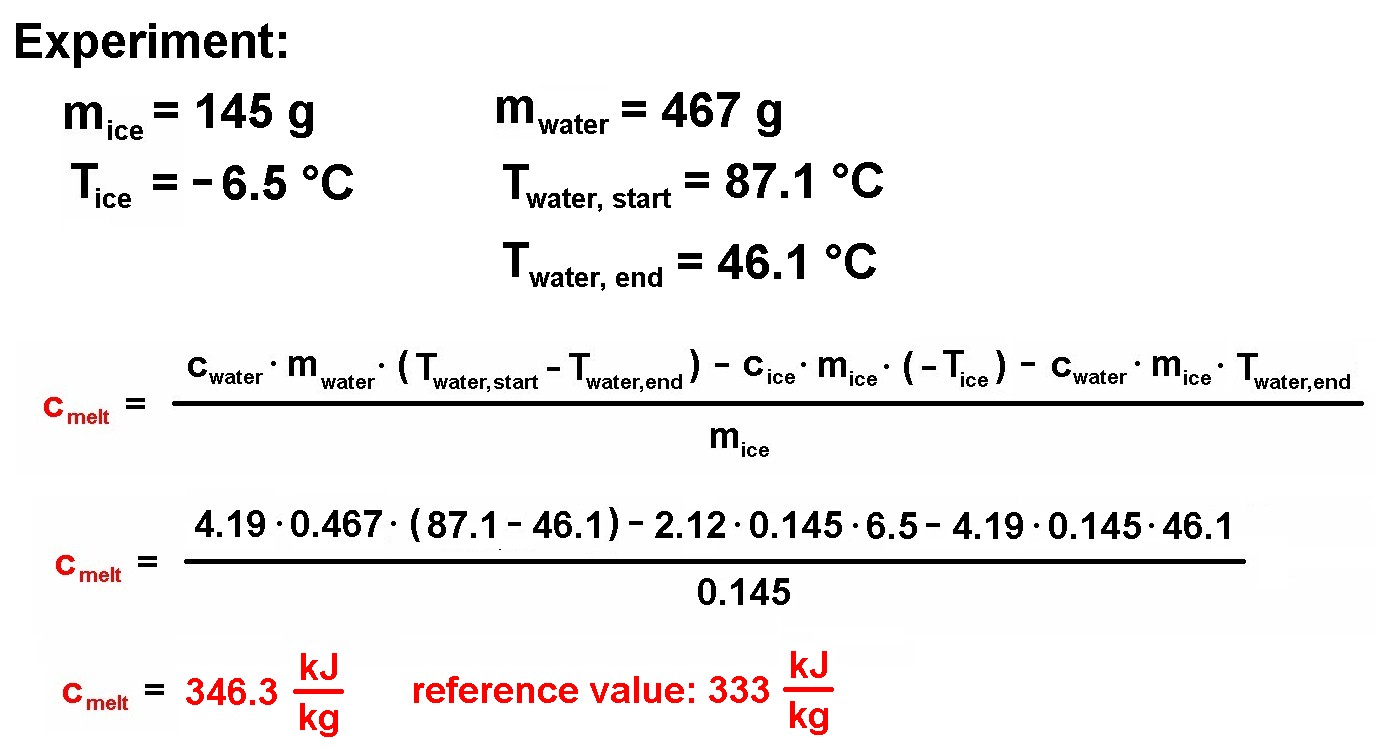
Mit meinen experimentell bestimmten 346.3 kJ zum Schmelzen von 1 Kilogramm Eis liege ich recht nahe am Sollwert 333 kJ/kg, Heureka 😉

 

---

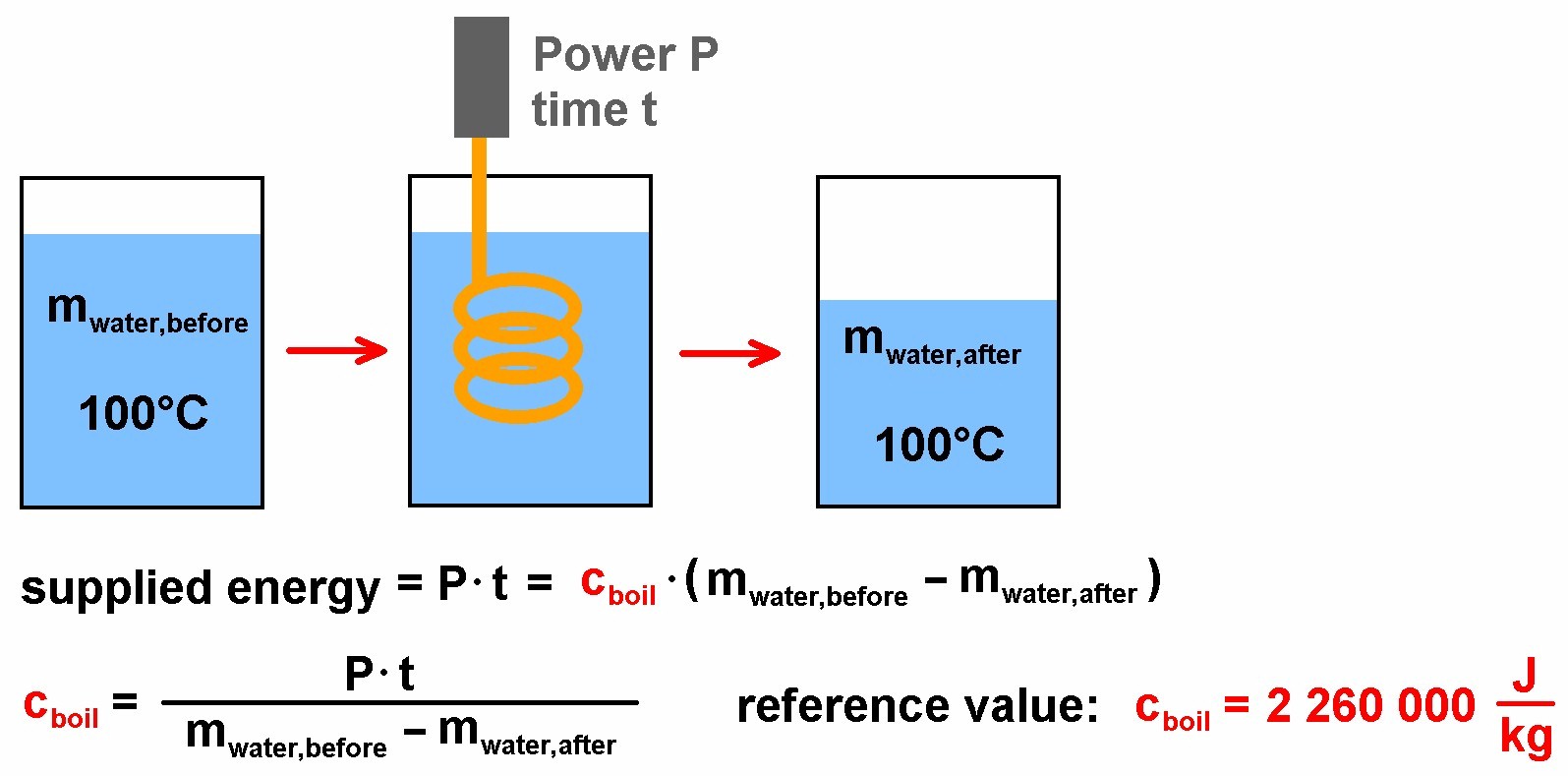
Im zweiten Teil des Versuchs geht es nun um die Verdampfungswärme von Wasser, also jener Energie, die zur Umwandlung von 1 kg siedenden Wassers in Dampf vonnöten ist.

Sie sollte bei 2260 kJ/kg liegen, also noch einmal ca. um den Faktor 7 größer als die Schmelzwärme. Der Versuch sieht schematisch wiefolgt aus:

Zum Erhitzen des Wassers habe ich mir auf willhaben.at einen günstigen Wasserkocher mit einer Leistung P = 300 W besorgt:

Dieser ist bereits angekommen und so konnte ich den Versuch durchführen. Als Waage musste ich allerdings meine Arduino-Waage verwenden, weil erstens die 5 kg Küchenwaage zu wenig sensibel auf geringe Gewichtsänderungen reagiert und zweitens sich die Waage nach einiger Zeit von selbst ausschaltet.

Die tatsächliche Leistung überprüfte ich mittels Strommessung. Es ergab sich eine Stromstärke von 1.287 A bzw. eine elektrische Leistung von P = 296 W.

Der gesamte Aufbau:

Hier kochte das Wasser bereits und die Waage zeigte sukzessive weniger an:

Nach etwas mehr als 10 Minuten war auf dem Display meiner Arduino-Waage dann folgender Masseverlust abzulesen:

Die Messwerte für den Masseverlust Δm in Abhängigkeit von der Zeit t:

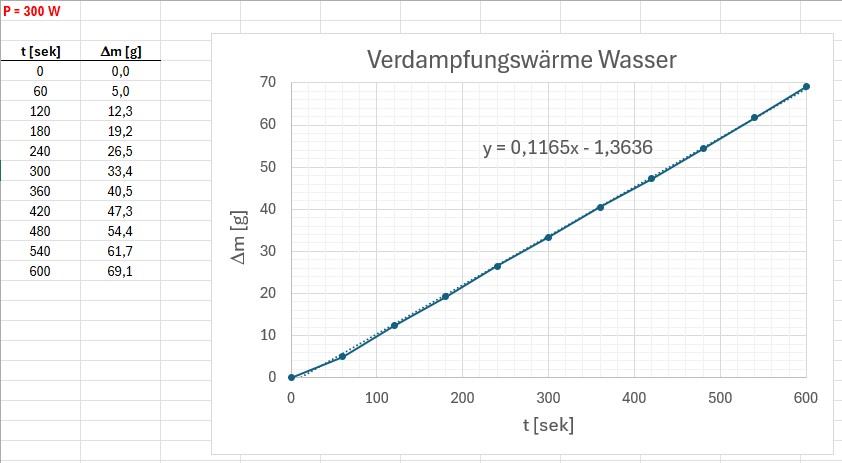
Dieser betrug also rund 0.1165 g/sek. Daraus konnte dann unter Berücksichtigung der 296 W Leistung die Verdampfungswärme von Wasser berechnet werden:

Die prozentuelle Abweichung vom Sollwert beträgt etwa 12 %, was nicht unbedingt berauschend ist. Aber vielleicht bekommt ja jemand von den Nachahmern einen besseren Wert heraus, viel Spaß beim Experimentieren 😉

Das Youtube-Video reiche ich wie immer nach…