In diesem experimentellen Beitrag soll es um die Bestimmung der Höhe eines Hochhauses auf unterschiedliche Arten gehen. Ich habe mich für das 6-stöckige Haus, in dem mein Bruder wohnt, entschieden.

Bestimmung mittels Luftdruck
In der ersten Variante bestimmen wir die Haushöhe mittels Luftdruckmessung. Der Luftdruck nimmt ja mit zunehmender Höhe exponentiell ab. Auf Meereshöhe beträgt er etwa 1 bar = 1000 mbar = 100000 Pa. Hier die kurze Herleitung der barometrischen Höhenformel:
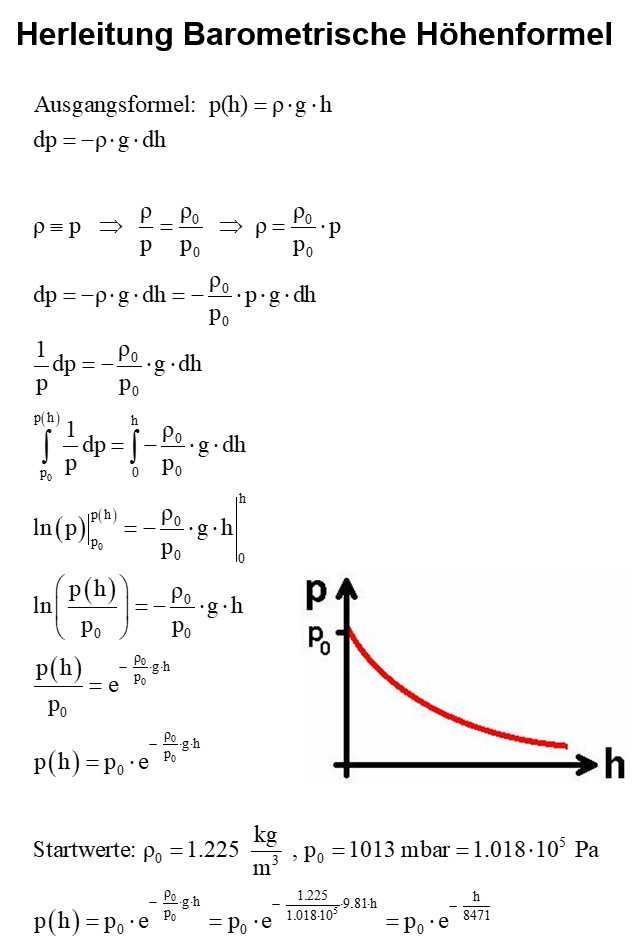
Im nächsten Schritt geht es um die Frage der Druckabnahme pro Meter Höhengewinn und zwar in einer Seehöhe von rund 360 m (= mein Standort). Dazu benötigen wir die Ableitung der barometrischen Höhenformel p(h) nach der Höhe h, also dp/dh:
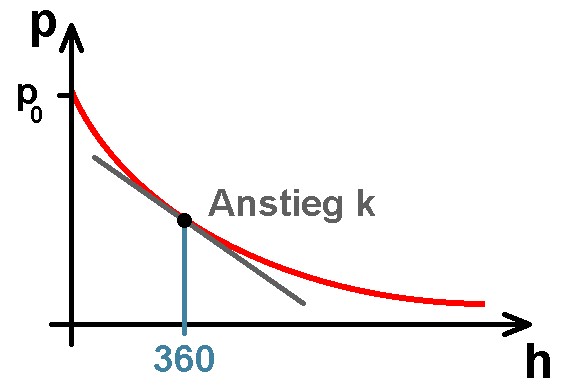

Bei mir in Graz beträgt also die Druckabnahme ca. 11.5 Pa pro Meter. Um jetzt auf die Höhe des Hauses zu kommen, muss ich nur die Druckänderung p(Boden) minus p(Hochhaus) in Pascal durch 11.5 dividieren, voila…
Den Luftdruck messe ich mit dem Sensor MPRLS von Adafruit. Diesen habe ich einmal für ein anderes Experiment auf Amazon gekauft. Die Verarbeitung und Ausgabe erfolgt mit einem Arduino:
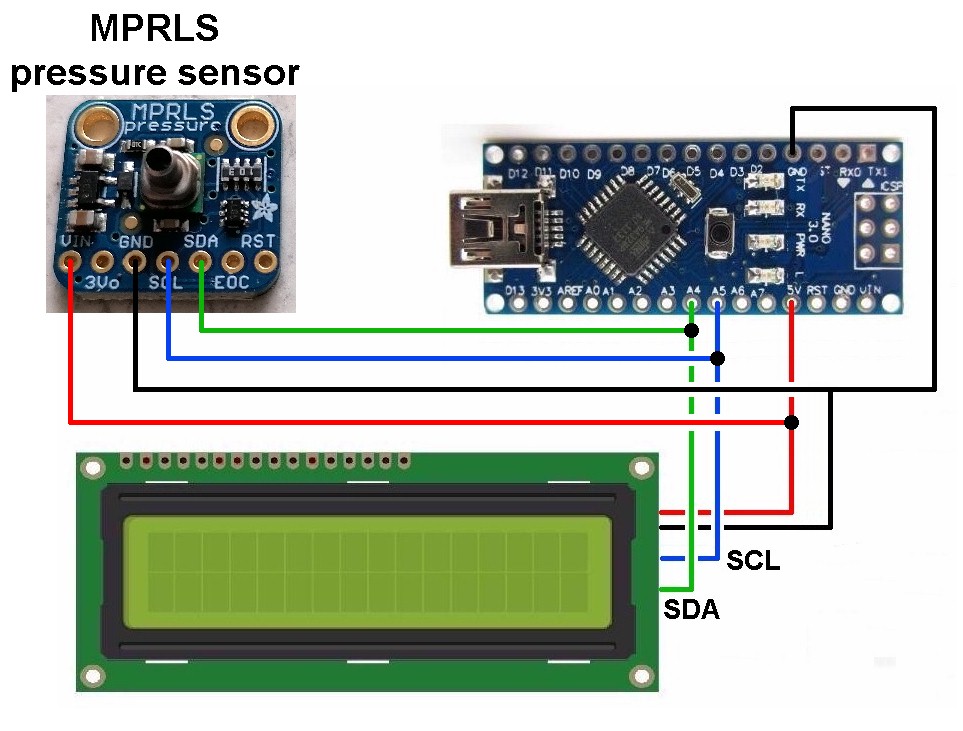



Damit ich eine einigermaßen ruhige und wenig schwankende Druckausgabe erhalte, berechne ich den Mittelwert aus 40 Druckmessungen und gebe diesen dann am Display aus. So schwankt der Druck bei konstanter Höhe nur um 0.01 – 0.03 mbar, also 1 – 3 Pascal.

Der Arduino-Code:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 |
/*! * @file mprls_simpletest.ino * * A basic test of the sensor with default settings * * Designed specifically to work with the MPRLS sensor from Adafruit * ----> https://www.adafruit.com/products/3965 * * These sensors use I2C to communicate, 2 pins (SCL+SDA) are required * to interface with the breakout. * * Adafruit invests time and resources providing this open source code, * please support Adafruit and open-source hardware by purchasing * products from Adafruit! * * Written by Limor Fried/Ladyada for Adafruit Industries. * * MIT license, all text here must be included in any redistribution. * */ #include <Wire.h> #include "Adafruit_MPRLS.h" #include <LiquidCrystal_I2C.h> LiquidCrystal_I2C lcd(0x27,16,2); // set the LCD address to 0x27 for a 16 chars and 2 line display. ACHTUNG: Adresse kann auch 0x3F sein !!! // Anschlüsse: // GND - GND // VCC - 5V // SDA - ANALOG Pin 4 // SCL - ANALOG pin 5 // You dont *need* a reset and EOC pin for most uses, so we set to -1 and don't connect #define RESET_PIN -1 // set to any GPIO pin # to hard-reset on begin() #define EOC_PIN -1 // set to any GPIO pin to read end-of-conversion by pin Adafruit_MPRLS mpr = Adafruit_MPRLS(RESET_PIN, EOC_PIN); float pressure_hPa; // ============ // == SETUP == // ============ void setup() { Serial.begin(115200); Serial.println("MPRLS Simple Test"); if (! mpr.begin()) { Serial.println("Failed to communicate with MPRLS sensor, check wiring?"); while (1) { delay(10); } } Serial.println("Found MPRLS sensor"); lcd.begin(); // initialize the lcd lcd.backlight(); lcd.setCursor(0,0); lcd.print("Drucksensor"); lcd.setCursor(0,1); lcd.print("MPRLS"); delay(3000); lcd.setCursor(0,0); lcd.print(" "); lcd.setCursor(0,1); lcd.print(" "); } // =========== // == LOOP == // =========== void loop() { pressure_hPa = 0.0; for(int i = 1; i <= 40;i++) { pressure_hPa = pressure_hPa + mpr.readPressure(); delay(20); } pressure_hPa = pressure_hPa / 40.0; Serial.print("Pressure (mbar): "); Serial.println(pressure_hPa); //Serial.print("Pressure (PSI): "); //Serial.println(pressure_hPa / 68.947572932); lcd.setCursor(0,0); lcd.print(pressure_hPa); lcd.print(" mbar "); delay(500); } |
Zum Messvorgang: Ich werde mit dem Barometer den Luftdruck am Boden und dann im 5-ten Stockwerk messen. Die Differenz in Pascal geteilt durch 11.5 ergibt dann wie gesagt die Höhe h.
Druck am Boden:

Druck im 5-ten Stockwerk:

Einfache Berechnung der Hochhaushöhe:

Bestimmung mittels Trigonometrie

Schüler behaupten ja (teilweise zu Recht), dass man das in der Schule Gelernte überhaupt nie brauchen kann. Ich trete hier den Gegenbeweis an und bestimme die Haushöhe mittels Trigonometrie.
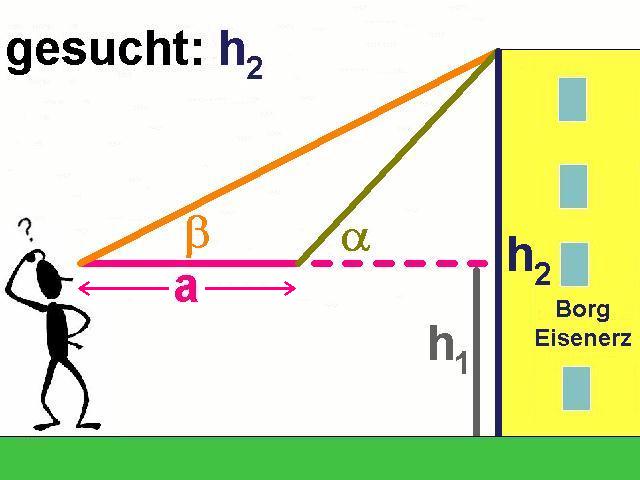
Zur Messung: Ich werde die beiden Winkel α und β mittels meines selbstgebauten Pendelquadranten bestimmen.
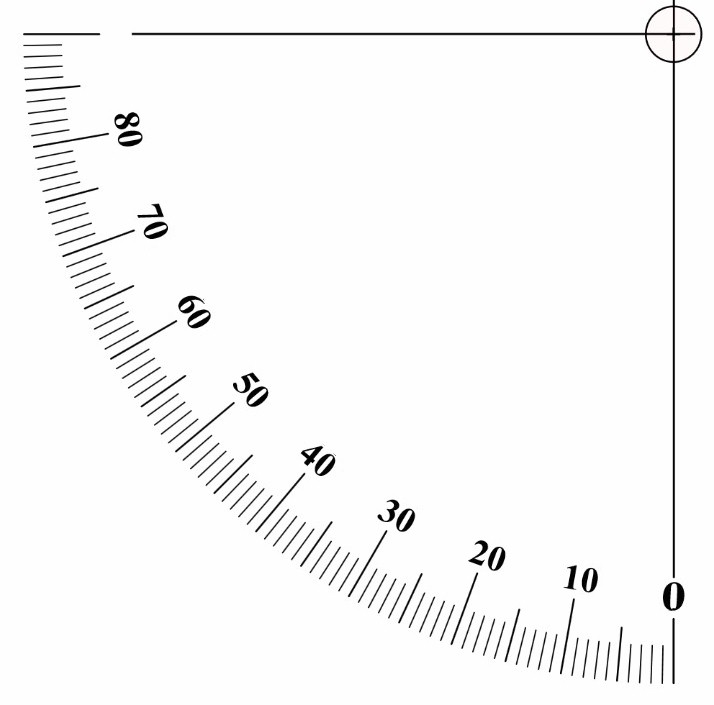



Zusätzlich kenne ich die Strecke a dank Google maps.
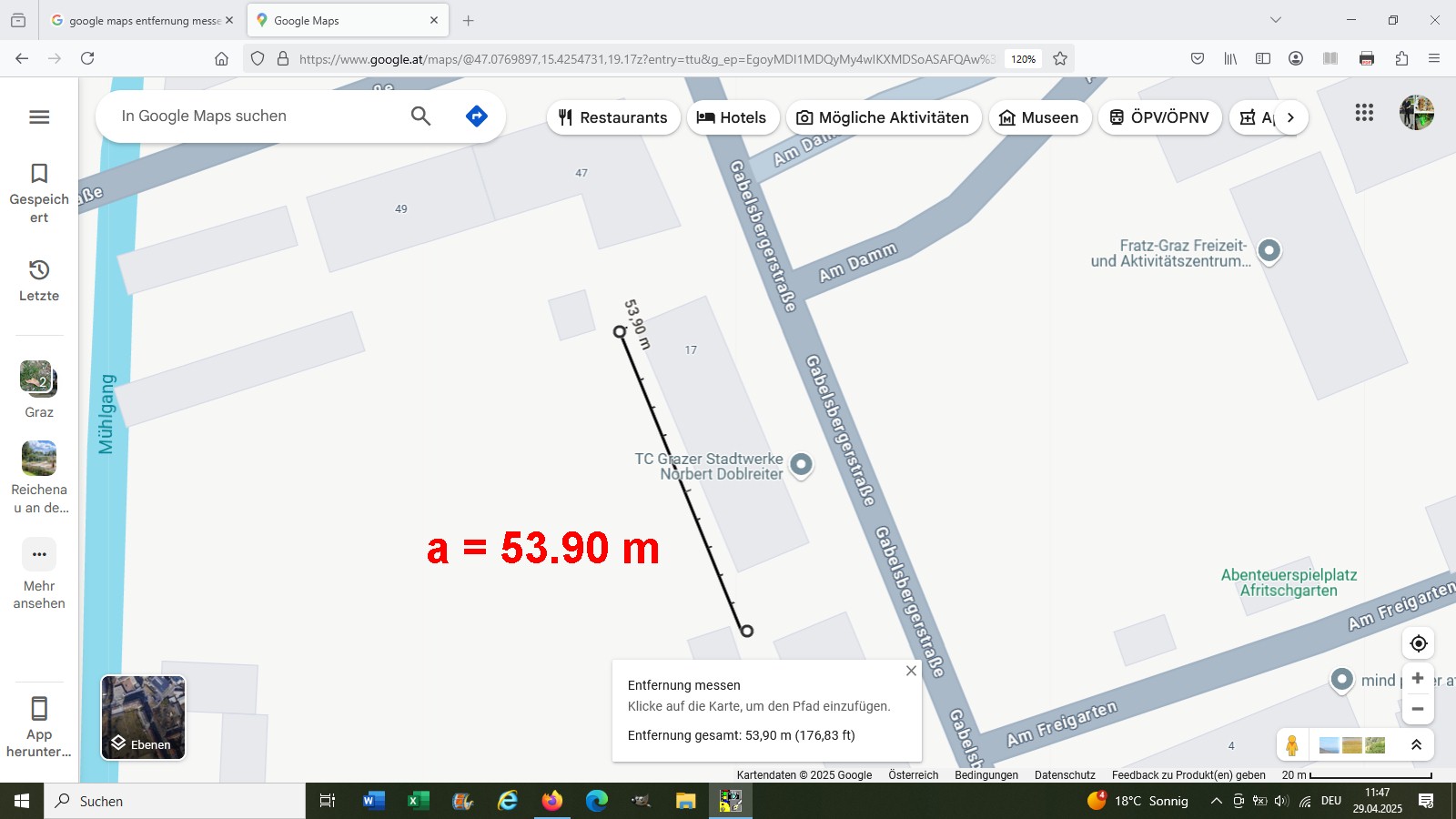
Der Ort zur Messung des Winkels β:



Ergebnis: β = 11.5°


Der Ort zur Messung des Winkels α:


Ergebnis: α = 33.5°

Nun der kurze mathematische Lösungsweg zur Bestimmung der Höhe y bzw. der Haushöhe h2:
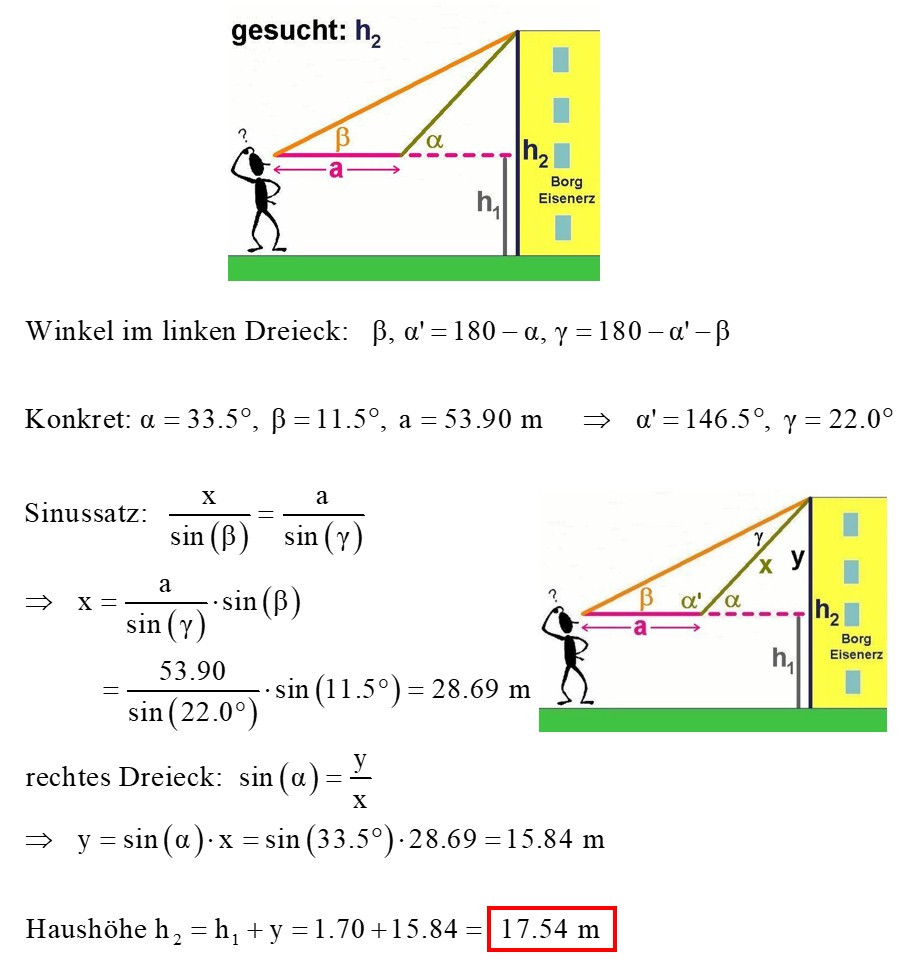
Bestimmung mittels freien Falls
Ohne Luftwiderstand beschleunigen frei fallende Körper gleichmäßig mit der Beschleunigung a = g = 9.81 m/s². Für diesen Bewegungstyp gelten die Beziehungen: a = g = konstant, v = g · t und s = 1/2 · g · t². Wir benötigen hier zur Bestimmung der Haushöhe die letzte Formel.
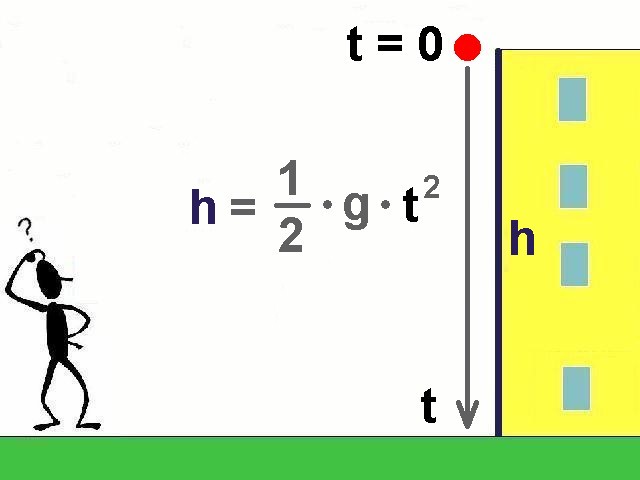
Mein Bruder wird von seinem Balkon im 5-ten Stock aus auf Kommando einen Ball (Golfball bzw. Tennisball) fallen lassen und ich stoppe die Zeit t für den freien Fall. Deshalb zwei unterschiedliche Bälle weil ich auch überprüfen möchte, ob der Luftwiderstand bereits eine größere Rolle spielt. Der Golfball müsste ja etwas schneller am Boden ankommen als der Tennisball, mal schauen.

Vielen Dank nochmals an meinen Bruder, welcher mich bei diesem Experiment unterstützte 😉

Mit der Software Tracker bestimmte ich den frame, bei dem mein Bruder den Golfball fallen ließ und den frame, bei dem der Ball am Boden aufkam:
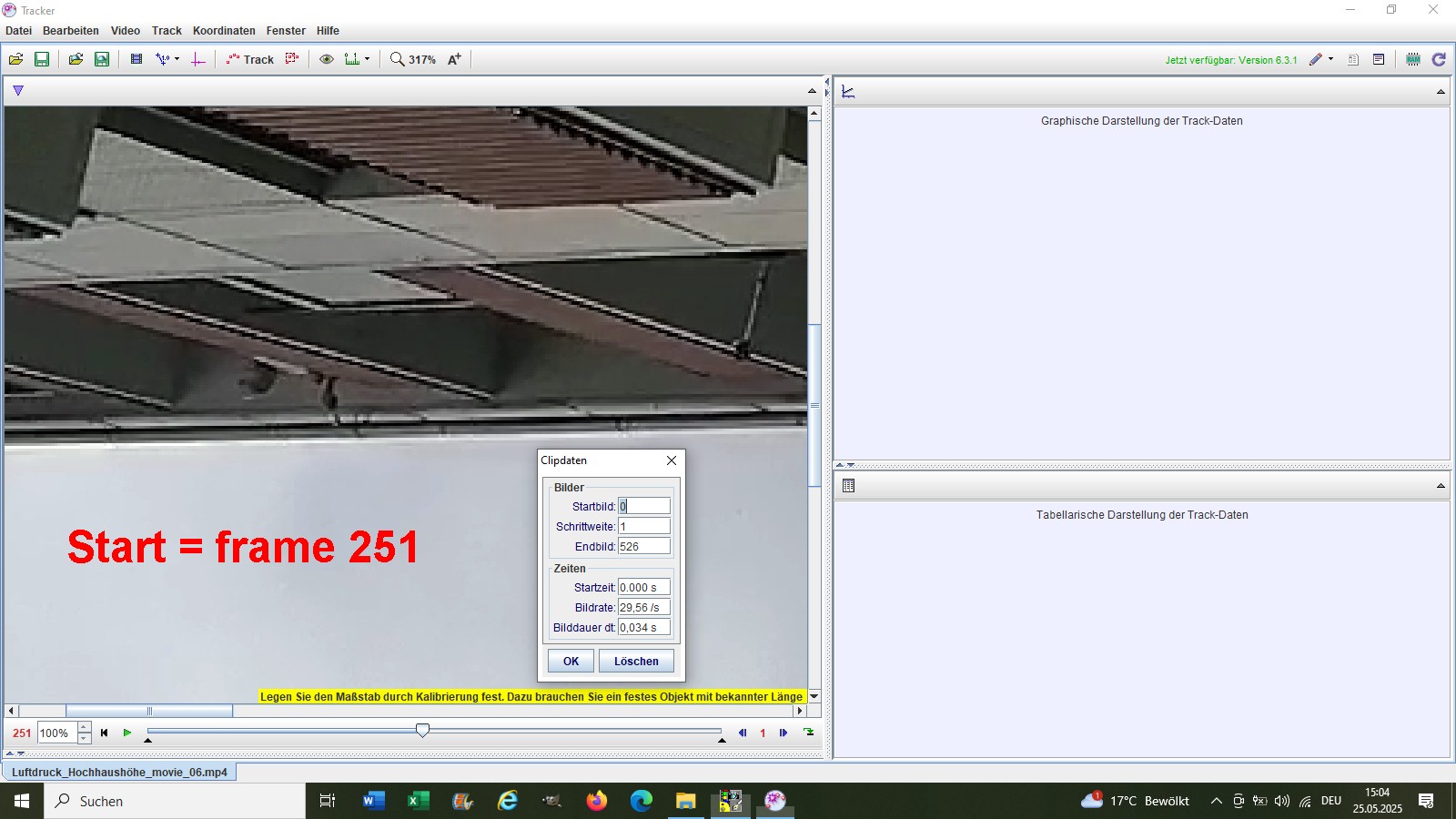
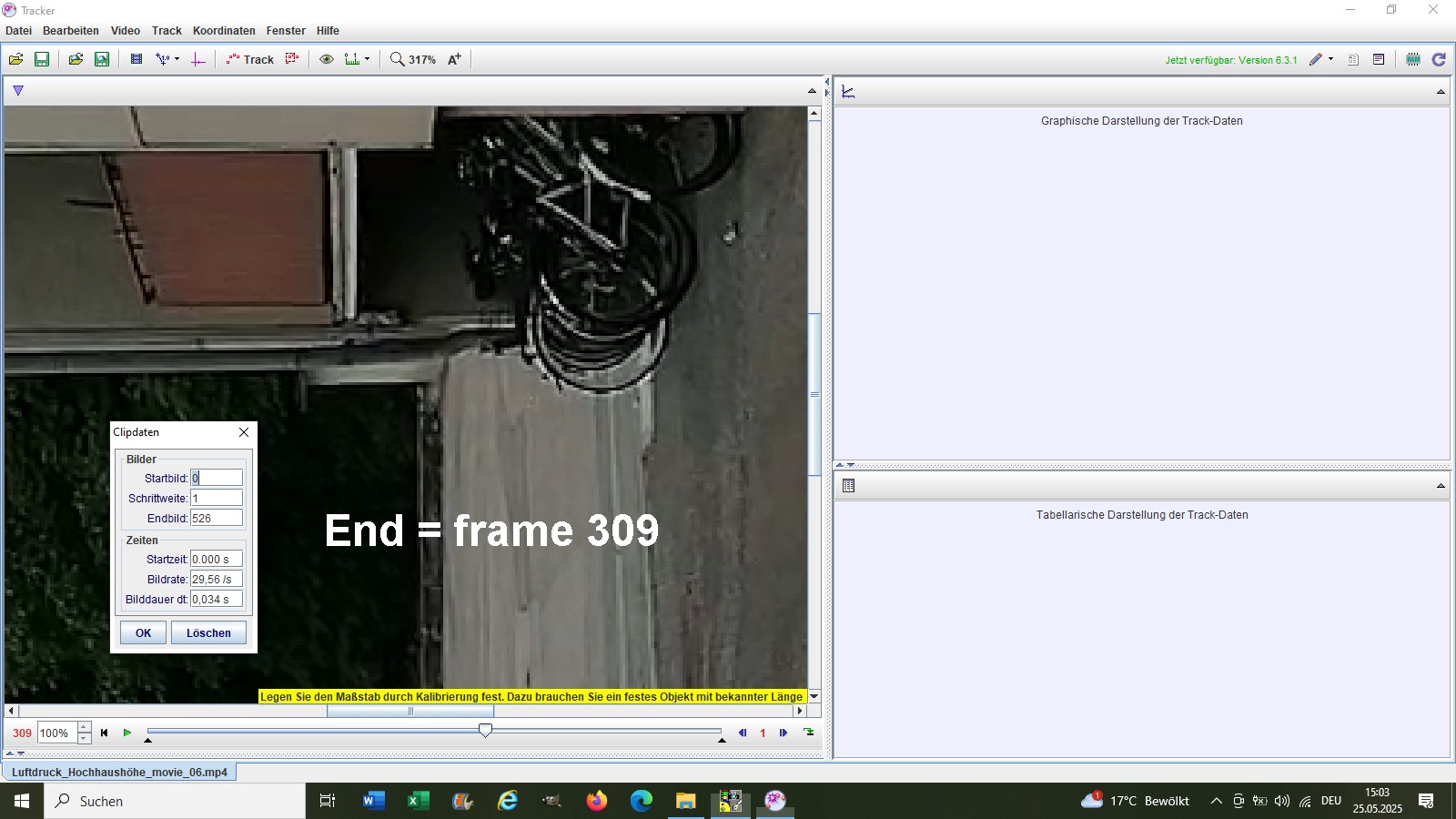
Diese 58 frames entsprachen bei einer Bildrate von 30 fps einer Zeitspanne von 1.933 sek:

Die drei experimentellen Ergebnisse liegen alle um die 18 m, was ein sehr plausibler Wert für den 5-ten Stock ist. Heureka…

