Angenommen es befindet sich in einer abgeschlossenen Kammer nur bis zur Hälfte Wasser. Dann können die energiereichsten Wassermoleküle die Flüssigkeit verlassen und in den gasförmigen Zustand übergehen. Andererseits werden gasförmige Wassermoleküle wieder kondensieren. Bei einer bestimmten Temperatur T bildet sich oberhalb der Flüssigkeit Dampf mit einem bestimmten Druck pDampf, dem Dampfdruck.

Dieser Druck hängt natürlich von der Flüssigkeit, aber auch entscheidend von der Temperatur T ab. Je höher die Temperatur, desto mehr Wassermoleküle können in die gasförmige Phase übergehen und desto größer ist der Dampfdruck pDampf. Die sog. Clausius–Clapeyron–Gleichung beschreibt den Dampfdruck in Abhängigkeit von T. Sie wurde 1834 von Émile Clapeyron entwickelt und später von Rudolf Clausius aus den Theorien der Thermodynamik abgeleitet. Es ergibt sich ein exponentieller Zusammenhang:

Jetzt sieht man im Graph, dass bei 100°C der Dampfdruck rund 1000 mbar beträgt. 100°C sind aber auch gleichzeitig die Siedetemperatur von Wasser auf Meereshöhe. Und tatsächlich besteht ein direkter Zusammenhang zwischen Dampfdruck und Siedetemperatur. Ist nämlich der Dampfdruck bei einer bestimmten Temperatur gleich dem äußeren Druck, so siedet die Flüssigkeit bei dieser Temperatur. Was passiert aber am Mount Everest? Dort beträgt ja der äußere Druck deutlich weniger als 1000 mbar. Demnach siedet dort Wasser bereits bei geringerer Temperatur, konkret bei rund 70°C. Beobachte ich also eine Flüssigkeit, die siedet, so ist der Dampfdruck gleich dem äußeren Druck. Genau diesen Umstand nutze ich bei der experimentellen Bestimmung des Dampfdrucks von Wasser (siehe unten).

Wo kommt diese Dampfdruckkurve vor? Im Phasendiagramm p(T) bildet sie die Grenze zwischen flüssiger und gasförmiger Phase:

Der Tripelpunkt TP ist jener Punkt, bei dem alle drei Phasen (fest-flüssig-gasförmig) zur gleichen Zeit vorkommen. Der kritische Punkt KP bzw. die zugehörige kritische Temperatur ist jene Grenze, oberhalb derer man Gas nicht mehr verflüssigen kann, egal wie man den Druck auch erhöht. Anhand des Phasendiagramms kann man auch schön den Zusammenhang Siedetemperatur-äußerer Druck erkennen. Dazu erhitzen wir einmal bei 1 bar Umgebungsdruck und einmal bei 0.3 bar Umgebungsdruck Wasser, bis es siedet. Am Mount Everest siedet es wie gesagt schon früher bei 70°C, da die Dampfdruckkurve früher erreicht wird:

Zum Thema Dampfdruck noch ein Gedankenexperiment: Angenommen wir haben einen Druckbehälter und darin befindet sich nun bei einer bestimmten Temperatur T ein Gas. Komprimiert man nun das Gas, so steigt der Druck p an und zwar solange, bis der Dampfdruck pDampf erreicht ist. Dann beginnt das Gas zu kondensieren und es bildet sich zunehmend die flüssige Phase. Solange die flüssige Phase und die gasförmige Phase koexistieren, solange bleibt der Druck auch bei voranschreitender Kompression gleich dem Dampfdruck. Erst wenn das letzte Gas in die flüssige Phase übergetreten ist und nur noch Flüssigkeit vorliegt, steigt der Druck immens an. Dies deshalb, weil ja Flüssigkeiten nahezu inkompressibel sind!

Diesen Versuch kann man bei verschiedenen Temperaturen T durchführen. Je höher die Temperatur, desto später (also bei höherem Druck) wird das Gas zu kondensieren beginnen.

Beträgt die Temperatur T > Tkritisch, so erfolgt auch bei noch so starker Kompression bzw. bei noch so hohem Druck keine Verflüssigung mehr. Die kritische Temperatur von Wasser beträgt zum Beispiel 374°C.
Nun aber zu den beiden Experimenten…
Variante 1:

Bei der Variante 1 zur Bestimmung der Dampfdruckkurve machen wir uns den Umstand zu Nutzen, dass eine Flüssigkeit dann siedet, wenn ihr Dampfdruck gleich dem äußeren Druck ist. Wir befüllen ein Gefäß halb mit Wasser bestimmter Temperatur T. Danach verschließen wir den Deckel luftdicht und saugen die Luft aus dem Gefäß. Der Innendruck sinkt und irgendwann wird Innendruck gleich dem Dampfdruck sein. Genau dann bilden sich in der Flüssigkeit Blasen und sie beginnt zu sieden. Den Innendruck (= Dampfdruck) messe ich mit dem Sensor MPRLS und einem Arduino:



Den Druck reduziere ich mit einer Handvakuumpumpe, welche ich ebenfalls bei Amazon sehr günstig gekauft habe. Glücklicherweise befand sich im Koffer gleich der passende Vakuumbehälter mit zwei Schlauchanschlüssen (1x für die Pumpe und 1x für das Barometer).




Hier der gesamte Versuchsaufbau inkl. Wasserkocher:


Hier ist der Innendruck noch größer als der Dampfdruck, das Wasser siedet noch nicht:

Wenn der Innendruck bis zum Dampfdruck reduziert wurde, beginnt das Wasser zu kochen:

Die Messergebnisse:

Wie man anhand des Graphen erkennt, liegt die experimentell ermittelte Dampfdruckkurve sehr nahe an der Sollkurve. Unterhalb von rund 40°C konnte ich keinen Dampfdruck mehr ermitteln, da ich mit der Handvakuumpumpe keinen geringeren Druck als ca. 80 mbar erzielen konnte.
Variante 2:
Das Prinzip der zweiten Variante ist simpel: Man postiert ein umgedrehtes und fast mit Wasser voll gefülltes Reagenzglas in einem Topf mit Wasser. Nur am oberen Ende des Reagenzglases soll sich zu Beginn bei Raumtemperatur eine kleine Luftblase befinden. Nun erhitzt man das Wasser und misst die Höhe der Luftblase. Diese sollte mit zunehmender Temperatur bzw. zunehmendem Dampfdruck wachsen. Der Innendruck in der Luftblase setzt sich aus dem Partialdruck der eingeschlossenen Luft und dem Dampfdruck des Wassers zusammen. Vergrößert sich das Volumen der Luftblase mit zunehmender Wassertemperatur, so nimmt der Partialdruck der Luft ab und dafür steigt der Dampfdruck des Wassers. Der Gesamtdruck in der Luftblase kann mittels der Höhe der Wassersäule h im Reagenzglas bestimmt werden. Er ist gleich dem äußeren Luftdruck (z.B. 970 mbar) minus dem hydrostatischen Druck der Wassersäule, also pro Zentimeter Höhe h minus ca. 1 mbar.

Die für dieses Experiment benötigten Teile habe ich auf Amazon entdeckt:



Das bestellte Laborstativ ist inzwischen angekommen und so konnte ich den Versuch durchführen. Beim Auspacken hatte ich tatkräftige Unterstützung von shady, dem Hund meiner Tochter 😉



Hier der Aufbau auf meinem Küchenherd:



Am Reagenzglas habe ich Zentimetermarkierungen angebracht:

Zu Beginn betrug die Höhe der Luftblase genau 1 cm und die Wassersäule h = 13.5 cm.

Mit zunehmender Temperatur vergrößerte sich die Luftblase am oberen Ende des Reagenzglases:






Das Problem bei dem Experiment war, dass ich einen starken Temperaturgradienten hatte und die Wassertemperatur oben im Inneren des Reagenzglases schon deutlich geringer war. Während das Wasser im Topf bereits kochte, hatte ich im oberen Teil des Reagenzglases noch deutlich niedrigere Temperaturen. Dadurch verschwanden die sich bildenden Blasen bei ihrem Aufstieg im Reagenzglas (siehe letztes Bild).


Dies war auch der Grund, warum ich nur Dampfdrücke mit maximal 616 mbar messen konnte. Dies würde einer Wassertemperatur von 85°C entsprechen, was ich mir sehr gut vorstellen kann.
Hier nun die konkreten Auswertungen und Berechnungen des Dampfdrucks:



Verglichen mit der ersten Variante zur Bestimmung der Dampfdruckkurve ist dieser Versuch problematischer eben durch die zu geringe Temperatur im Reagenzglas. Demnach würde ich die Variante mit der Handvakuumpumpe bevorzugen…
Dampfdruckerniedrigung durch Salz
Warum streut man eigentlich im Winter Salz? Der Grund dafür liegt in der Dampfdruckerniedrigung durch Salz. Reines Wasser besitzt folgendes Phasendiagramm:

Der Schmelzpunkt liegt unter Atmosphärendruck bei 0°C und der Siedepunkt bei 100°C.
Fügt man nun dem Wasser aber Salz zu, so wird der Dampfdruck erniedrigt, sprich die Dampfdruckkurve von Salzwasser liegt tiefer:
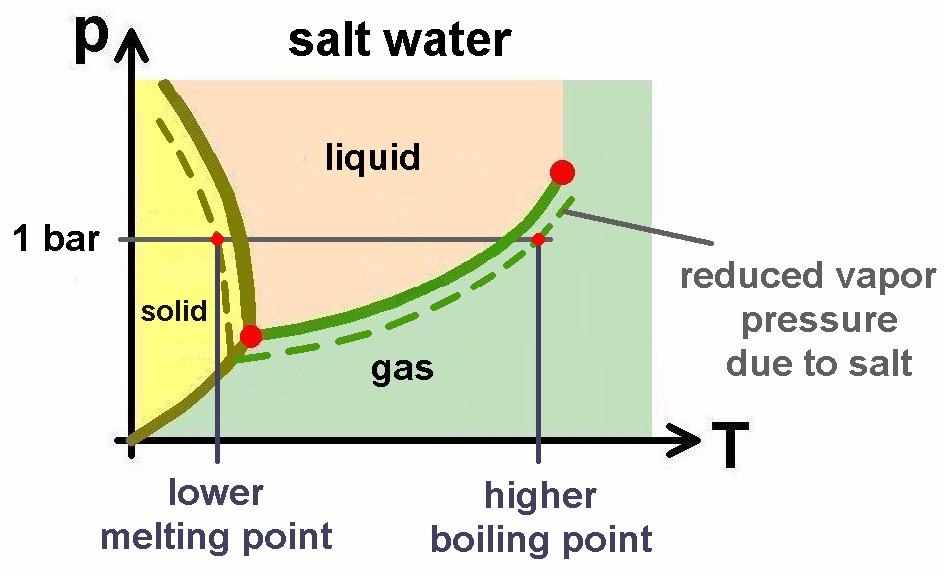
Dies hat zur Folge, dass Salzwasser erst bei einer höheren Temperatur als 100°C zu kochen beginnt bzw. erst unterhalb von 0°C gefriert, zum Beispiel erst bei –3°C. Genau dies ist der Grund, warum man im Winter Salz streut, denn dann gefriert das Salzwasser nicht mehr so leicht.
Die Siedepunkterhöhung durch Salz untersuche ich im folgenden Experiment. Dazu gebe ich 1 Liter Wasser in den Wasserkocher und bestimme zunächst noch ohne Salz die Siedetemperatur.




Sie liegt bei 99.7°C:

Danach füge ich immer mehr Salz dem Wasser zu und bestimme jeweils die gestiegene Siedetemperatur. Das verdampfte Wasser fülle ich inzwischen wieder auf…


Bei einer Salzkonzentration von 59.5 g/l betrug die Siedetemperatur zum Beispiel bereits 101.1 °C:

Zum Schluss die Siedetemperatur in Abhängigkeit von der Salzkonzentration:
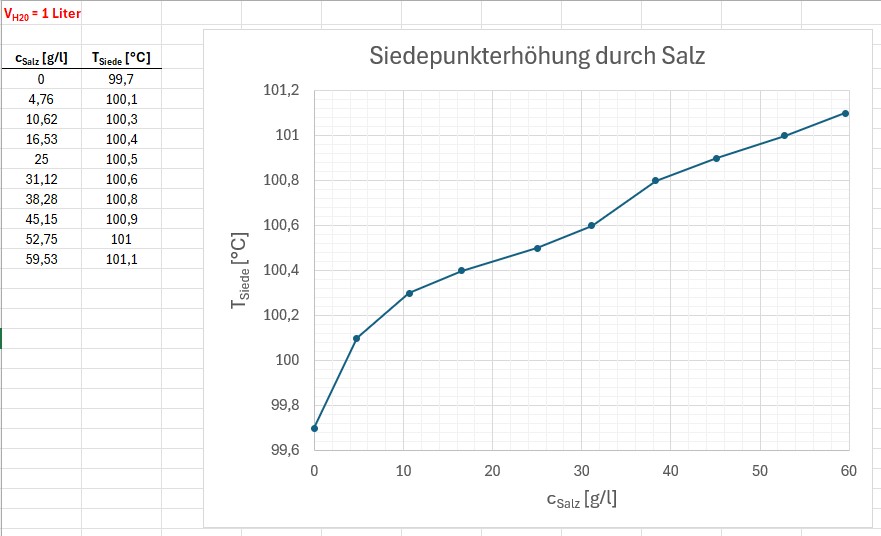
Für die Siedepunkterhöhung in Abhängigkeit von der Konzentration gibt es auch eine Formel, jene von Raoult. Hier gibt man die Konzentration c des gelösten Stoffs in mol/l an. Aber aufgepasst, hier geht es um die aufgelöste, getrennte Teilchenanzahl. Wenn sich also 1 mol NaCl löst, so haben wir es mit 2 · mol gelösten Teilchen zu tun! Die Raoult’sche Formel lautet allgemein:

Konkret für Salz in Wasser ergibt sich daraus folgende Gleichung:

Mit dieser Beziehung kann ich nun meine experimentellen Ergebnisse mit den theoretischen Sollwerten vergleichen:

Die Steigung meines Graphen scheint gut zu stimmen, nur habe ich zu Beginn bei geringen Konzentrationen einen zu starken Anstieg…

