Man kann es kaum glauben, aber die Größe eines Atoms lässt sich mit Hausmitteln bestimmen. Man benötigt hierfür nur
- Benzin
- Sonnenblumenöl
- eine Pipette
- ein sehr kleine Spritze (1 mL = 1 cm³)
- ein Backblech mit erhöhtem Rand
- Wasser
- Bärlappsporen (Lycopodium)
- Plastikdose mit schraubbaren Deckel
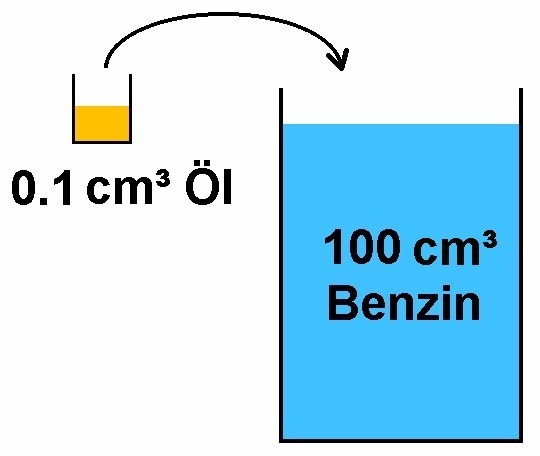
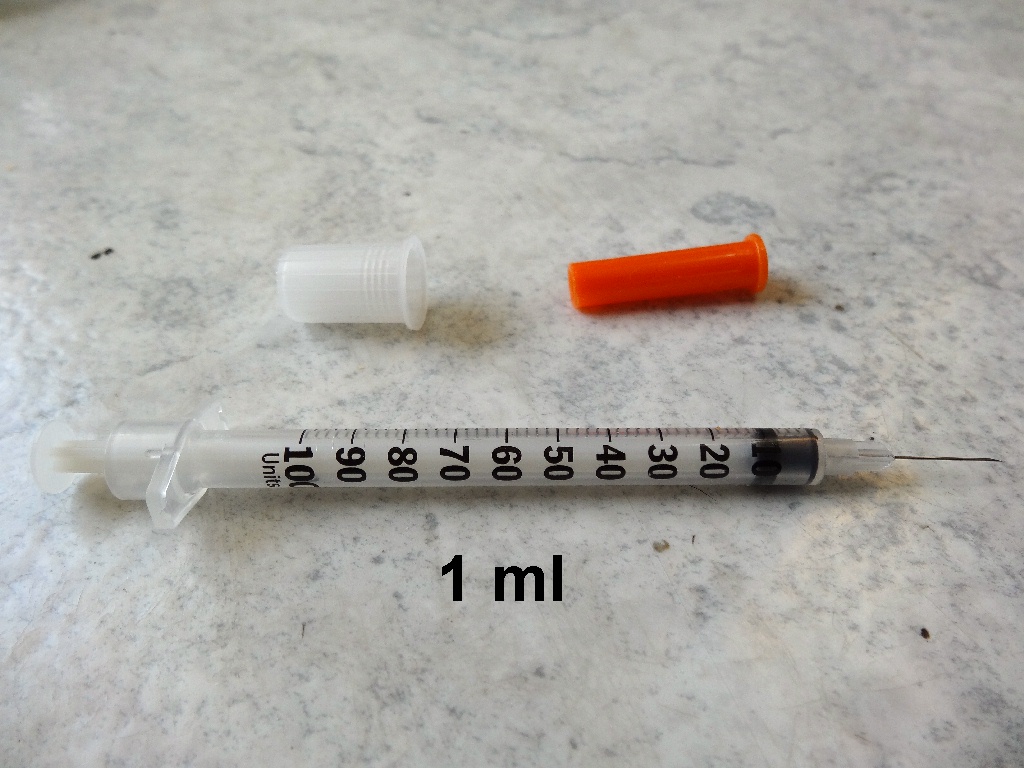
Zur Durchführung des Versuchs: Zu Beginn benötigt man 100 cm³ Benzin. Danach gibt man nur 0.1 cm³ Öl dem Bezin hinzu. Als nächstes muss man das Volumen eines Tropfens aus der Pipette bestimmen. Hierzu befüllt man die Pipette mit Bezin und tropft dann solange in eine geöffnete 1 mL-Spritze, bis diese voll ist. Konkret waren bei mir 67 Tropfen aus der Pipette vonnöten, bis die 1 mL-Spritze voll war. Demnach besitzt 1 Tropfen aus der Pipette ein Volumen von 1/67 cm³.
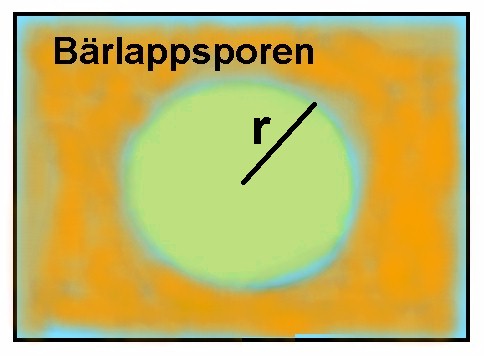
Nun befüllt man das Backblech ca. 1 cm hoch mit Wasser. Die Bärlappsporen füllt man in eine Plastikdose mit schraubbaren Deckel. In diesen Deckel stößt man ca. 5-10 mal mit einer dünnen Nadel. Danach bestreut man das Wasser mit Bärlappsporen, sodass dieses einigermaßen gleichmäßig aber dünn mit Sporen bedeckt ist.
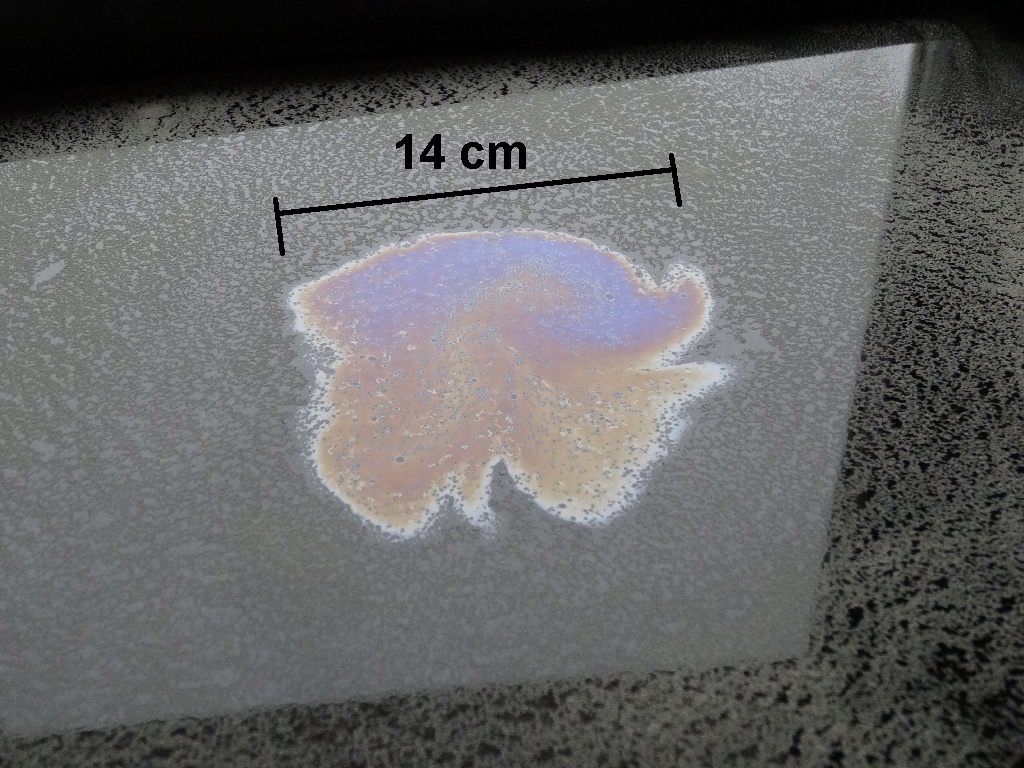
Jetzt befüllt man die Pipette mit dem Benzin/Öl-Gemisch und lässt danach einen einzigen Tropfen auf das Wasser/die Bärlappsporen fallen. Wenn alles richtig gemacht wurde, müsste sich eine ölige Kreisfläche ohne Sporen bilden. Deren Radius r bestimmt man mit einem Lineal. Konkret konnte ich r zu 7 cm ermitteln.
Wie kann man nun daraus die Atomgröße bestimmen? Nun, wir wissen das Volumen eines Pipettentropfens und zwar 1/67 cm³. Daran befinden sich durch das Mischungsverhältnis von 1:1000 nur 1/67000 cm³ Öl.
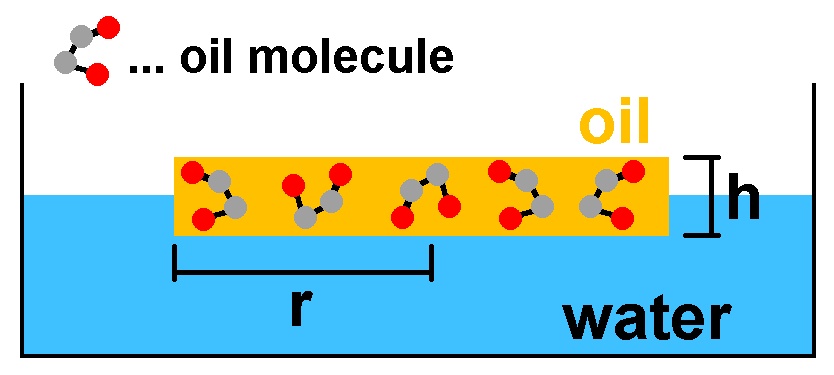
Das Ölvolumen entspricht aber auch der Kreisfläche * Ölschichtdicke h, also 7² · π · h = 1/67000. Daraus folgt für die Ölschichtdicke h = 9.7 · 10^ –8 cm = 9.7 · 10^ –10 m.
Sonnenblumenöl besteht großteils aus der Ölsäure (Triolein, C57–H104–O6). Nun geht man davon aus, dass die Ölschichtdicke h genau der Kantenlänge des Ölsäuremoleküls mit seinen 167 Atomen entspricht.
Diese 167 Atome benötigen also ein Volumen von h · h · h. Demnach benötigt 1 Atom (wir gehen jetzt einmal von 167 gleich großen Atomen aus) genau das Volumen h · h · h / 167. Die Kantenlänge d eines Atoms (dieses wird ebenfalls als Würfel angenommen) beträgt somit h / 3-te Wurzel von 167, konkret also
d = 1.76 · 10^ –10 m = 1.76 Angström.
Dieser Atomdurchmesser deckt sich erstaunlich gut mit den Literaturwerten.


Quelle: Wikipedia











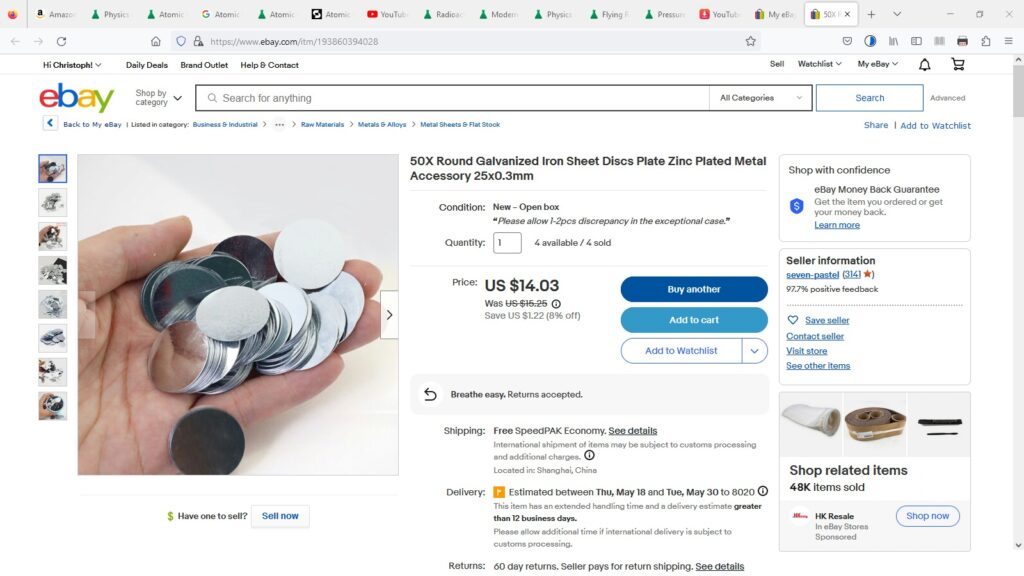
Einen netten ähnlichen Versuch habe ich noch auf Lager und zwar die einfache Dickenbestimmung einer Zinkschicht. Hierfür benötigt man Stahlplättchen, welche mit Zink überzogen sind. Meine habe ich günstig auf ebay.com gekauft.

Zum Entfernen der Zinkschicht wird Salzsäure benötigt. Zum Glück hatte ich noch eine vom Versuch „Protactiniumgenerator“ zuhause:

Das Experiment ist denkbar einfach: Man misst zuerst den Durchmesser der Stahlplättchen, um deren Fläche A zu bestimmen. In meinem Fall betrug der Durchmesser 24.6 mm und demzufolge der Radius 1.23 cm. Dies ergibt eine Fläche von A = 4.753 cm².

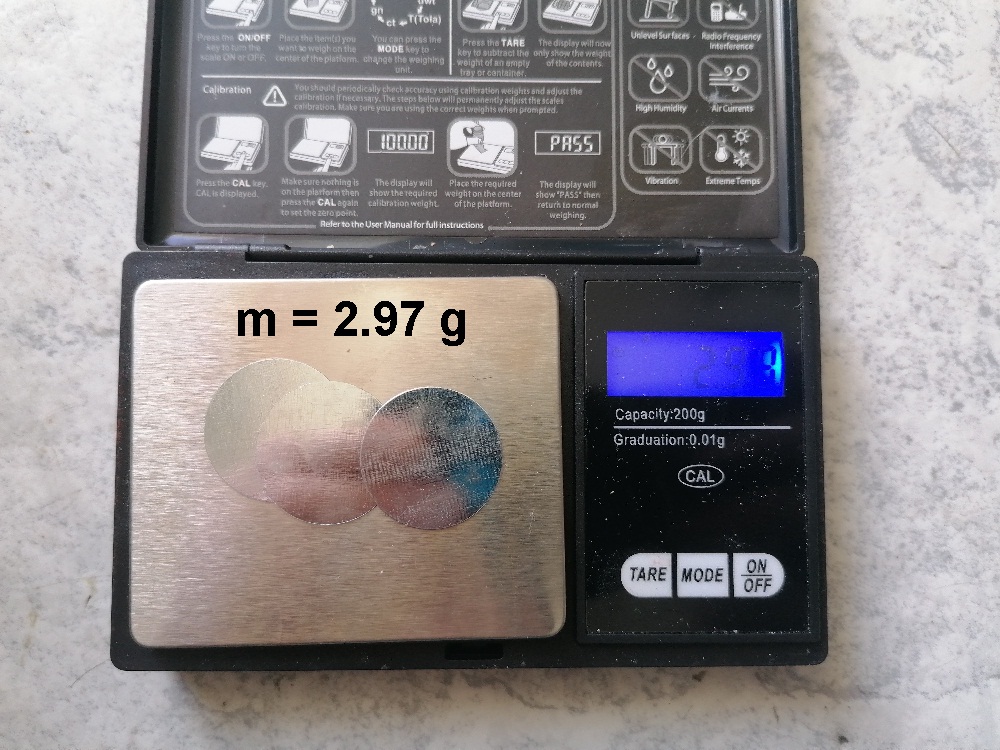
Danach wiegt man ein oder mehrere Metallplättchen auf einer Feinwaage ab. Drei Plättchen wogen bei mir 2.97 g.
Jetzt gibt man die Plättchen in die Salzsäure und wartet einige Zeit, bis die Zinkschicht durch die Säure entfernt wurde.


Zum Schluss wiegt man die Plättchen noch einmal. Bei mir waren es nach der Säurebehandlung nur noch 2.75 g.

Mittels der gesamten Massenänderung Δm kommt man auf die Massenänderung pro Seitenfläche, indem ich einfach Δm durch 6 (Seiten) dividiere. Dies sind bei mir 0.0367 g. Kennt man die Dichte von Zink (ρ = 7.14 g/cm³), so kann man diese Massenänderung pro Seite in ein Volumen umrechnen. Dies ergibt 0.00514 cm³. Dieser Wert entspricht genau dem entfernten Zinkvolumen V auf jeder Seitenfläche. Da wir aber auch die Fläche A des Metallplättchens kennen, kann man mittels Volumen V die Dicke d = V / A der Zinkschicht bestimmen. Das Ergebnis lautet: d = 10.8 µm.


