Unter einem idealen Gas versteht man ein Gas bei dem erstens die darin enthaltenen Teilchen kein Eigenvolumen besitzen und zweitens zwischen den Teilchen keine Kraft herrscht. Dies ist natürlich nur eine idealisierte Vorstellung. Echte, reale Gase kommen dieser nur bedingt nahe.
Welche Zustandsgrößen sind bei einem Gas wichtig? Nun, da wäre einmal das Volumen V, die Teilchenanzahl n, die Temperatur T und der Druck p. Für ein ideales Gas besteht ein sehr einfacher Zusammenhang zwischen diesen Größen und zwar die thermische Zustandsgleichung idealer Gase:
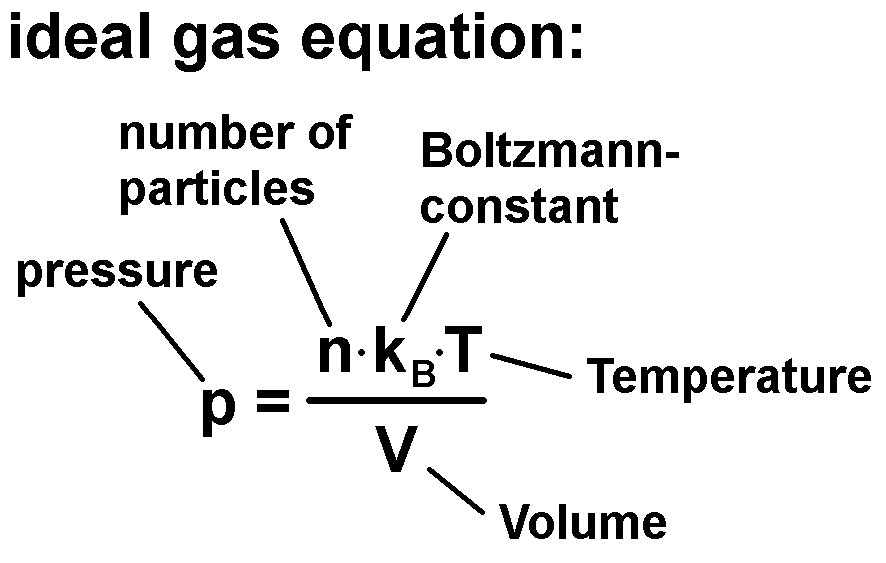
Diese Zustansgleichung beinhaltet noch die berühmte Boltzmannkonstante kB, welche zu Ehren des österreichischen Physikers Ludwig Boltzmann (1844 – 1906) benannt wurde. Er wirkte unter anderem in meiner Heimatstadt Graz.
In der Physik muss man oft vereinfachen bzw. idealisieren. In diesem Fall untersucht man das Verhalten eines idealen Gases, wobei bis auf zwei alle anderen Zustandsgrößen konstant bleiben. Dies führt uns zu den bekannten Gasgesetzen.
1.) Isotherm (T = konstant und stillschweigend auch die Teilchenanzahl n):
 Dieser Spezialfall führt uns zum Boyle-Mariotte-Gesetz p·V = konstant. Eine Halbierung des Volumens bedingt also bei konstanter Temperatur T und Teilchenanzahl n eine Verdopplung des Drucks.
Dieser Spezialfall führt uns zum Boyle-Mariotte-Gesetz p·V = konstant. Eine Halbierung des Volumens bedingt also bei konstanter Temperatur T und Teilchenanzahl n eine Verdopplung des Drucks.
Für den experimentellen Nachweis dieser Beziehung benötigt man lediglich eine Spritze (150 ml), einen Schlauch, einen 1/8″ auf 4 mm Adapter und ein Manometer (0-2 bar). All dies kann man zum Beispiel günstig auf aliexpress beziehen.






Herrscht etwa bei einem Volumen V = 150 ml ein Druck von 1 bar, so steigt dieser bei einer Reduzierung von V auf nur noch 75 ml auf 2 bar an.


2.) Isobar (p und n sind konstant):
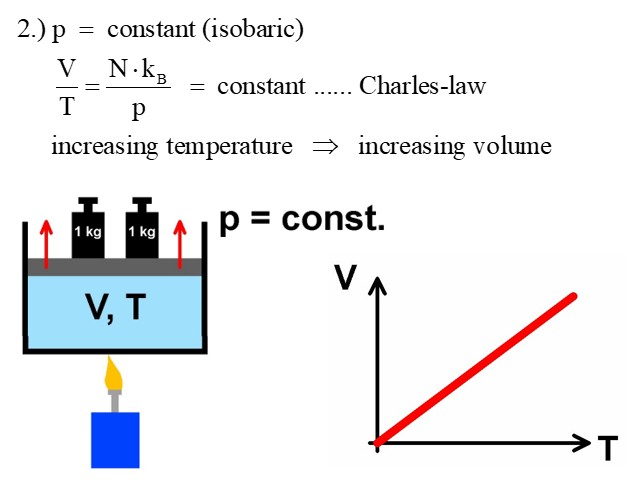
Bleibt der Druck p konstant, so vereinfacht sich die Zustandsgleichung zum Gasgesetz von Charles, welches V/T = konstant lautet. Bei einer Verdopplung der Temperatur wächst bei konstantem Druck das Volumen auf das Doppelte.
Zum experimentellen Nachweis eignet folgender sehr einfache Versuch: Eine Plastikflasche wird zunächst mit sehr heißem Wasser ausgespült. Danach schüttet man dieses wieder aus und verschließt schnell den Verschluss. Nun beginnt sich die Luft in der Flasche abzukühlen. In weiterer Folge drückt sich die Flasche von ganz alleine zusammen. Dadurch wird ihr Volumen reduziert. Der Druck bleibt aber innen einigermaßen konstant.
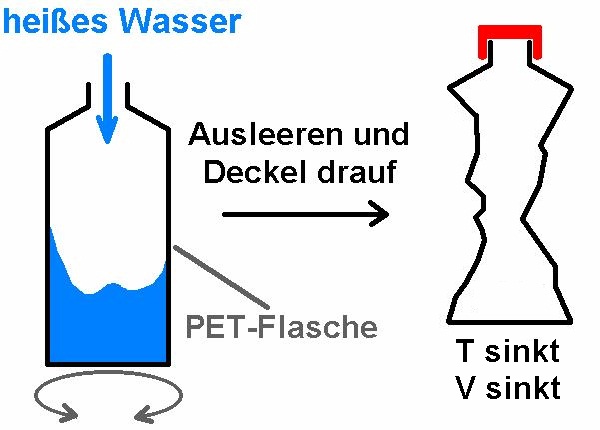
Die mit dem heißen Wasser erwärmte Flasche unmittelbar vor dem Verschließen:

Die Flasche nach dem Abkühlen:

Das Video zum Versuch liefere ich natürlich noch nach…
3.) Isochor (V und n sind konstant):
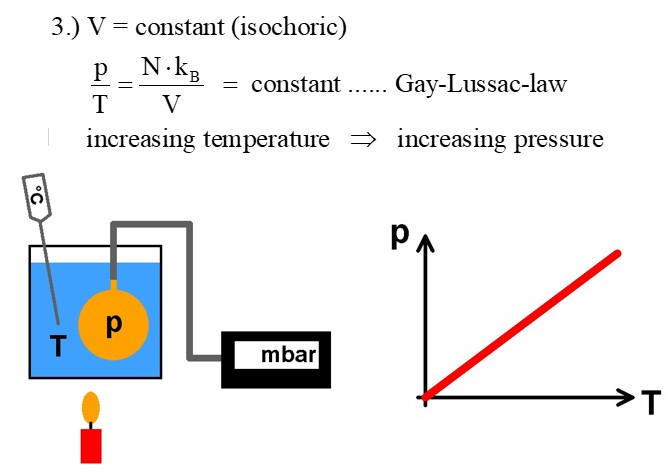
Lässt man das Volumen konstant, so gelangt man zum Gasgesetz von Gay-Lussac, welches p/T = konstant lautet. Erhöht man die Temperatur T eines konstanten Gasvolumens, so steigt der Druck p.
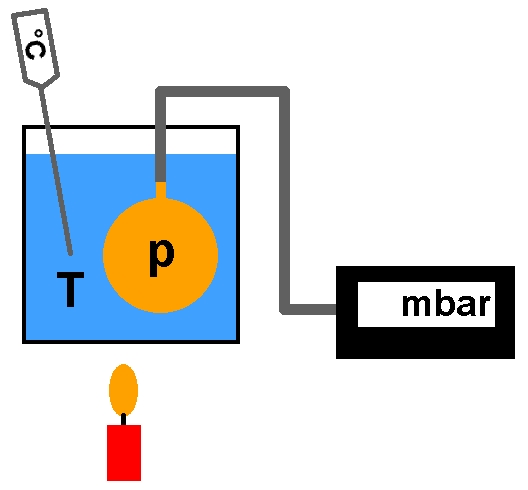
Für das entsprechende Experiment benötigt man eine Hohlkugel mit angelöteten Schlauchstutzen und ein Barometer zum Beispiel in Form des Sensors BMP085. Ausgelesen wird dieser von einem Arduino.









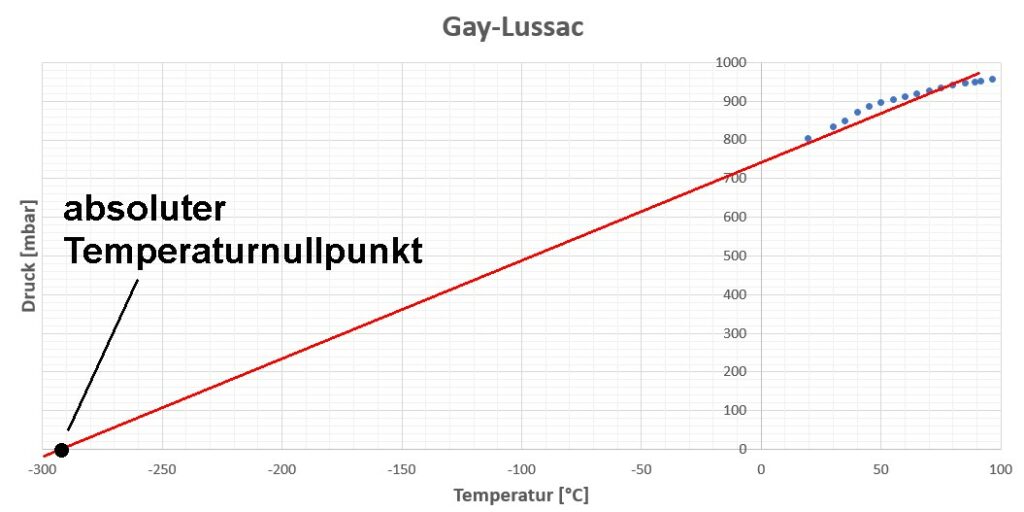
Trägt man die Drücke in Abhängigkeit von der Temperatur auf, so erhält man eine Gerade. Verlängert man diese in Richtung niedrigerer Temperatur, so kann man jene Temperatur ermitteln, bei der der Druck verschwindet. Dies ist genau beim absoluten Temperaturnullpunkt bei T = -273 °C = 0 Kelvin der Fall.

Einige Spielereien zu den Gasgesetzen:




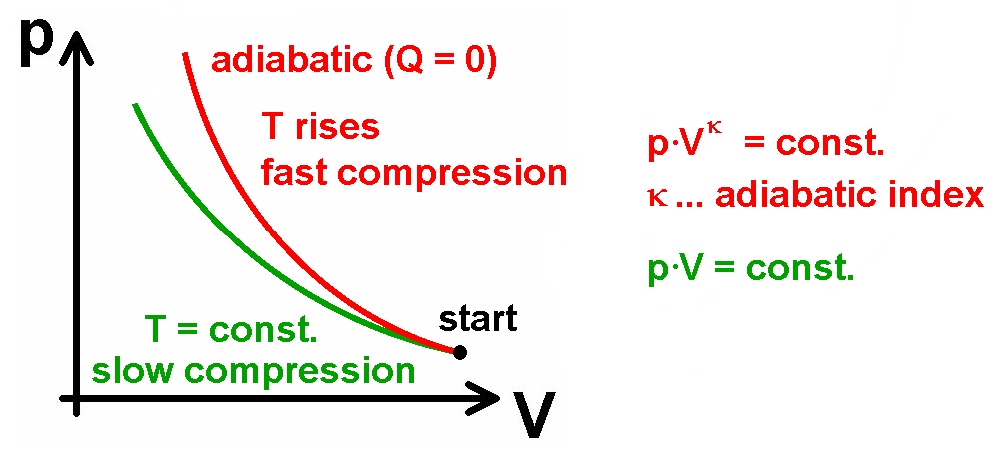
Bei der sog. adiabatischen Zustandsänderung fließt keine Wärme zu oder ab. Dies ist zum Beispiel dann der Fall, wenn sich der Zustand sehr schnell ändert. Nehmen wir den Fall einer zusammengedrückten Spritze. Drücke ich den Kolben nach unten, so werden die am Kolben reflektierten Gasteilchen nach dem Stoß eine höhere Geschwindigkeit und damit Temperatur besitzen. Geschieht die Kompression langsam, so fließt Wärme vom erwärmten Gas an die Umgebung und die Temperatur T bleibt konstant. Dies wäre der isotherme Spezialfall mit dem dazugehörigen Boyle-Mariotte-Gesetz p·V = konstant.
Drückt man allerdings den Kolben schnell nach unten, so hat das erwärmte Gas keine Möglichkeit, die Wärme an die Umgebung abzugeben. Es steigt dann also nicht nur der Druck aufgrund der Volumenreduzierung, sondern auch aufgrund der Temperaturerhöhung. Diese quasi doppelte Druckerhöhung wird durch den sog. Adiabatenexponent κ = cp / cV (mit den spezifischen Wärmekapazitäten cp und cV bei konstantem Druck bzw. Volumen) im Gasgesetz berücksichtigt, welches bei adiabatischer Zustandsänderung nun p·V ^κ = konstant lautet.
Der Wert des Adiabatenexponenten κ hängt vom Freiheitsgrad der Gasteilchen ab und der Freiheitsgrad eines Gasmoleküls hängt von der Geometrie und der Bindungsstärke der Atome ab. Unter einem Freiheitsgrad versteht man jede Form von Bewegung, in welcher Energie steckt. Gasmoleküle mit mehr Atomen besitzen einen höheren Freiheitsgrad, da sie auch kompliziertere Bewegungen vollführen können. Ein ideales, punktförmiges Gas besitzt nur die 3 Freiheitsgrade aufgrund der Translation, also der normalen Bewegung in x-, y- und z-Richtung. Bei mehratomigen Gasen kommen noch Freiheitsgrade aufgrund von Rotationen und Schwingungen hinzu. Zwischen dem Adiabatenexponent κ und der Anzahl der Freiheitsgrade f gilt folgender Zusammenhang: κ = (f + 2) / f.
Ein einatomiges Gas mit f = 3 besitzt demnach einen Adiabatenexponent κ = 5/3. Einen solchen beobachtet man etwa bei den Edelgasen Helium und Argon. Bei einem 2-atomigen Gas wie N2 oder O2 mit f = 5 ergibt sich κ = 7/5 = 1.4. Für Luft beträgt der Adiabatenexponent in der Tat rund κ = 1.4.
Ein schöner Versuch zum Thema adiabatische Kompression besteht aus einem Glaszylinder mit Kolben. Drückt man diesen sehr schnell nach unten, steigt wie oben geschildert neben dem Druck auch die Temperatur stark an. Auf diese Art können Temperaturen von über 500 °C erzielt werden. Dies reicht aus, um gewisse Stoffe zu entzünden. Dieser Effekt wird etwa beim Dieselmotor, welcher ja keine Zündkerzen besitzt, tagtäglich umgesetzt.
Auf Amazon bin ich auf folgendes günstige , wenngleich auch mit schlechter Bewertung versehene Angebot gestoßen:
Ich hoffe, es hält zumindest für einen Versuch 😉 Den umgekehrten Fall, also die Abkühlung durch adiabatische Expansion nützt man zum Beispiel bei der Wilson-Nebelkammer zur Sichtbarmachung radioaktiver Strahlung (siehe https://stoppi-homemade-physics.de/radioaktivitaet/nebelkammer/).
So, das Päckchen aus China ist eingetroffen und da mein Forscherdrang kaum zu bändigen ist, habe ich den Versuch zur adiabatischen Kompression gleich durchgeführt. Und allen Befürchtungen zum Trotz hat es gleich auf Anhieb funktioniert und der Kolben ist sogar heil geblieben 😉




Zum Schluss wie immer das Youtube-Video:

