Das Faradaysche Induktionsgesetz besagt, dass eine zeitliche Änderung des magnetischen Flusses dΦ/dt eine Induktionsspannung Uind ergibt. Bewegt man etwa einen Magneten vor einer Spule, so wird eine elektrische Spannung induziert. Dies ist das Prinzip eines Generators.

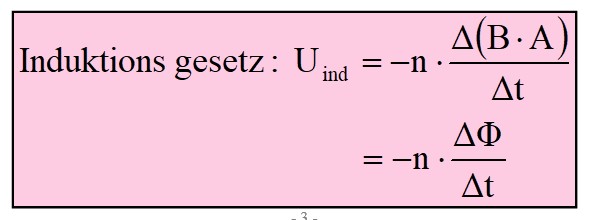
Dabei ist n die Anzahl der Windungen, B die magnetische Flussdichte und A der Querschnitt der Spule. Je größer die Änderung des magnetischen Flusses, desto höher die Induktionsspannung. Bewege ich also den Magneten langsam zur Spule, so ist Uind klein. Nähere ich den Magneten der Spule aber schnell, so kommt es zu einer hohen Induktionsspannung.
Jetzt wissen wir aber auch, dass eine stromdurchflossene Spule ein Elektromagnet ist, welcher also ein magnetisches Feld erzeugt. Der Induktionsspannung ist es aber nun egal, ob das sich ändernde Magnetfeld von einem Magneten stammt oder der stromdurchflossenen Spule selbst.
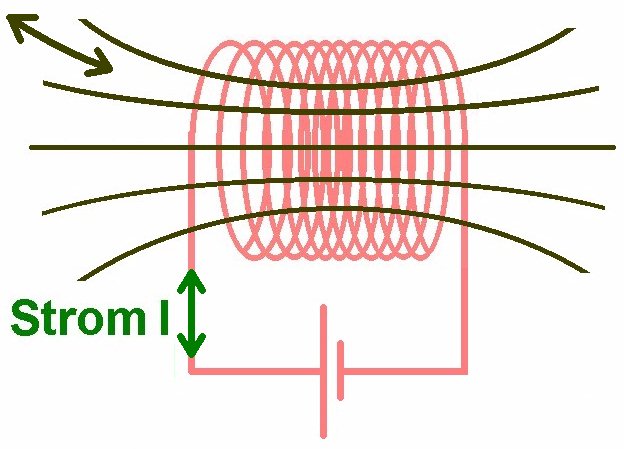
Es gilt aber ebenso wie bei einem Magneten, dass sich für eine Induktionsspannung Uind das Magnetfeld ändern muss. Erzeugt die Spule selbst das Magnetfeld, so muss sich also für ein Uind ≠ 0 die Stromstärke I durch die Spule ändern. Bei Gleichstrom (I = konstant) wird demnach keine Spannung induziert!
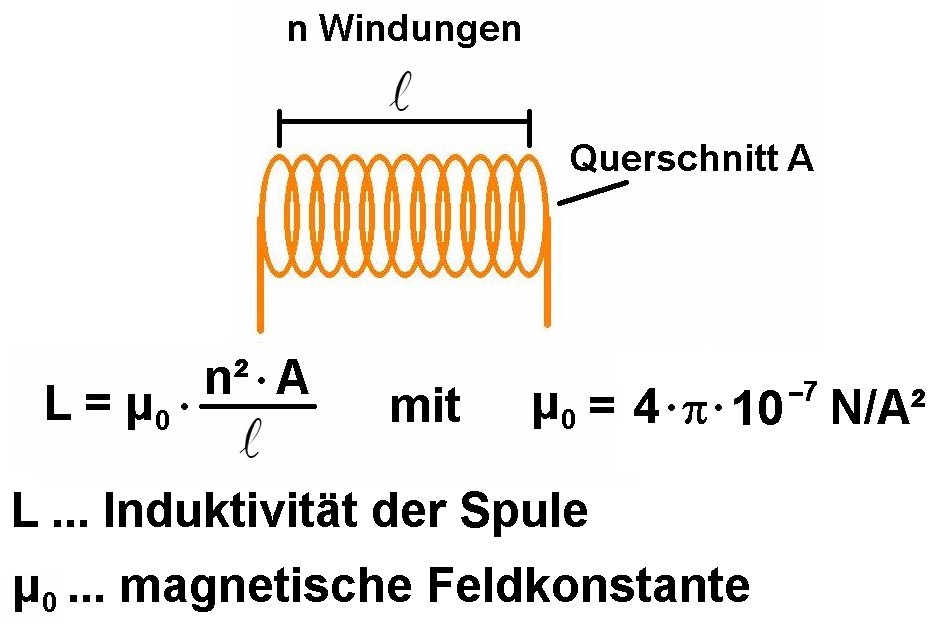
Für die magnetische Feldstärke H einer langen Zylinderspule gilt die Formel: H = n · I / l. Genau diese Beziehung benötigen wir für folgende Schritte:

Hier tritt also eine neue Kenngröße für Spulen in Erscheinung, die sog. Induktivität L mit der Einheit Henry. Für eine Zylinderspule an Luft (Permeabilität µr = 1) lautet also die Formel für die Induktivität:
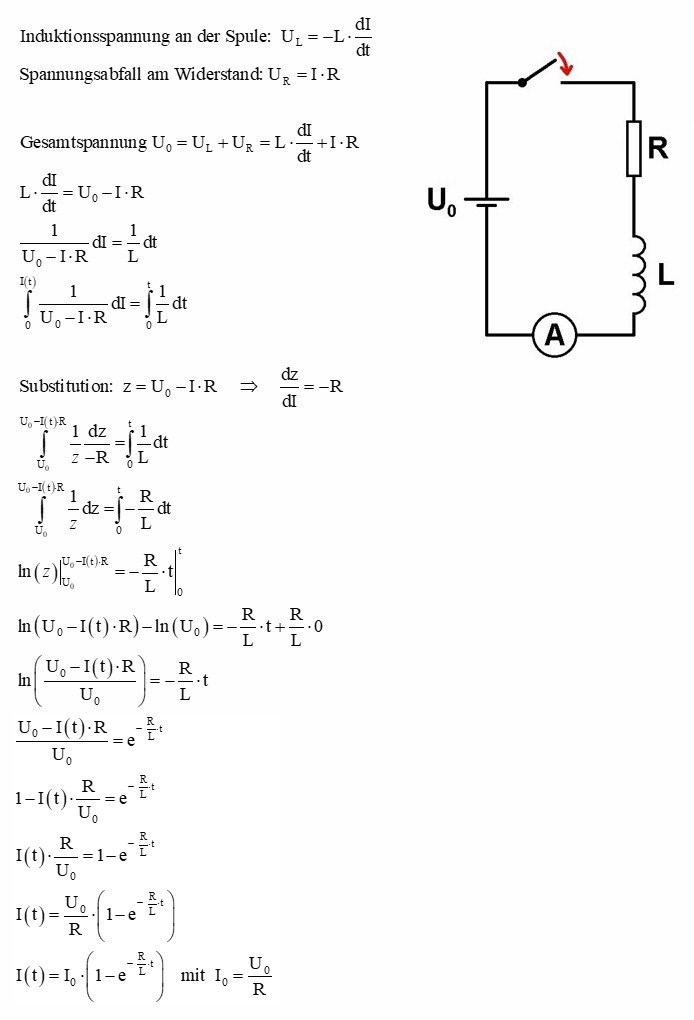
Was passiert nun, wenn wir eine Spule mit der Induktivität L an eine Gleichspannungsquelle klemmen und den Schalter schließen? Nun, die Stromstärke wird zu Beginn (stark) ansteigen. Eine sich schnell ändernde Stromstärke bedeutet aber ein großes dI/dt bzw. ΔI/Δt. Laut obiger Formel für die Selbstinduktion bedingt dies aber eine hohe Selbstinduktionsspannung. An der reinen Induktivität der Spule fällt also zu Beginn eine große (Anm.: Wie wir später noch sehen werden eigentlich die gesamte Batteriespannung) ab. Diese wirkt aber der Lenzschen Regel nach entgegen der Ursache und verhindert dadurch einen allzu schnellen Stromanstieg durch die Schaltung. Die Spule bremst also den Stromanstieg und zwar umso mehr, je größer ihre Induktivität L ist.
Mit den oben hergeleiteten Formeln können wir uns für folgende einfache Schaltung an die Berechnung der Stromstärke I(t) in Abhängigkeit von der Zeit t wagen:

Hier ein Beispiel für den Graphen I(t):
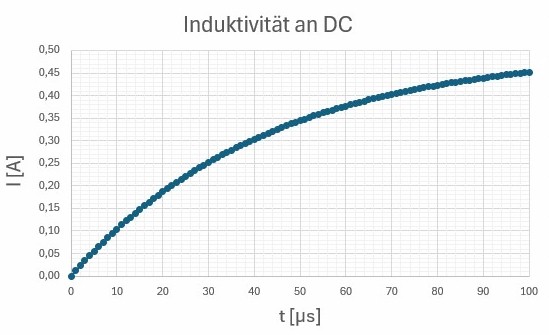
Die Stromstärke wächst also zu Beginn stark und dann flacht die Kurve immer mehr ab. Sie nähert sich dabei einem Grenzwert und zwar genau jener Stromstärke I = U0 / R, als würde die Schaltung nur aus dem ohmschen Widerstand R bestehen. Je größer R, desto schneller erreicht I seinen Grenzwert und je größer L, desto länger braucht sie.

Man kann den Stromverlauf auch sehr schön mit EXCEL simulieren:
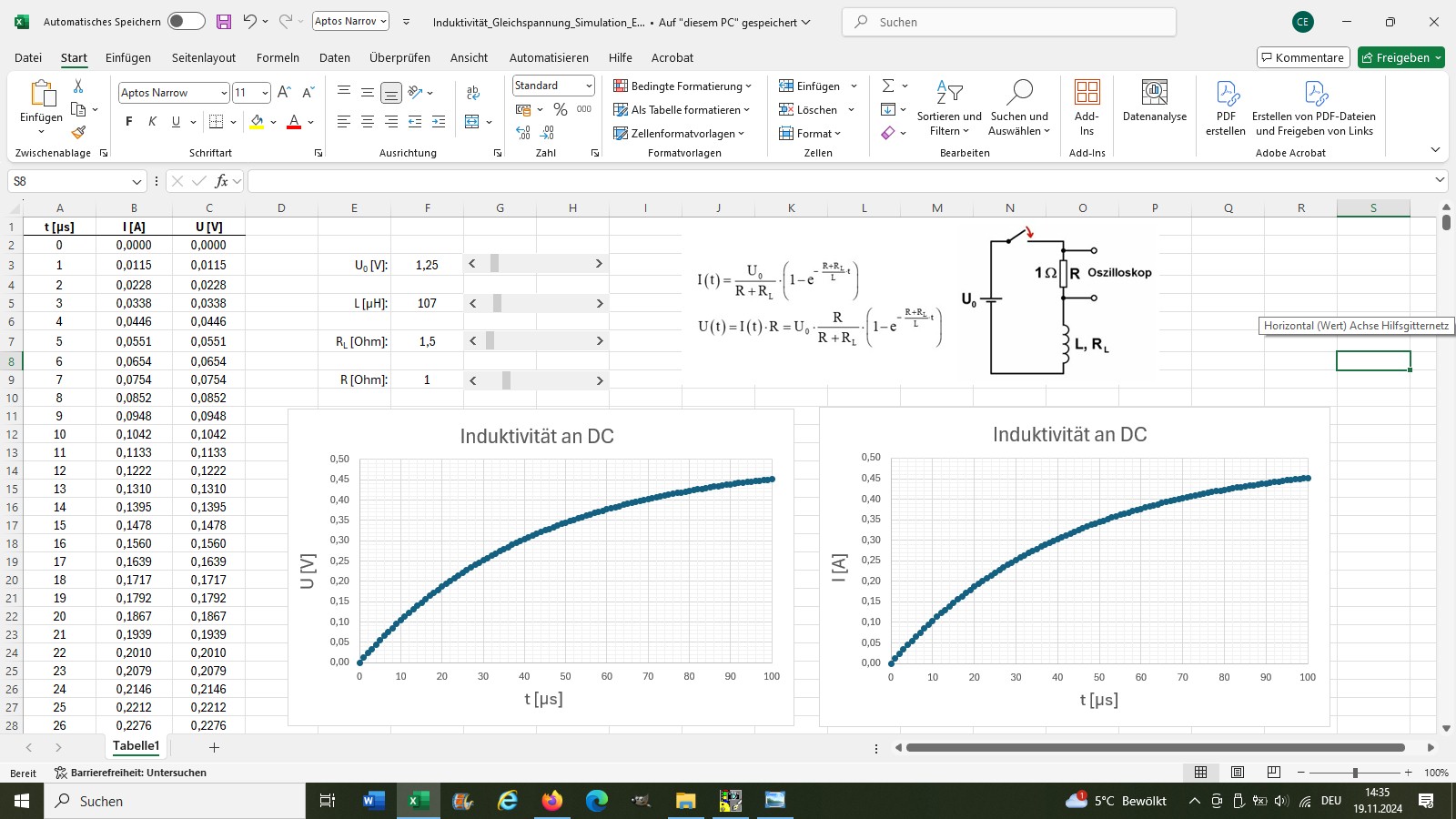
Genau diese obige einfache Schaltung werden wir experimentell umsetzen und aus den Kurvenverläufen I(t) die Induktivität L der Spule auf zwei Arten bestimmen.
Mit einem sog. Oszilloskop kann man zeitliche Spannungsverläufe U(t) aufzeichnen. Wir wollen aber den Stromverlauf I(t) verfolgen. Dies ist aber überhaupt kein Problem. Denn schließen wir das Oszilloskop an einen Widerstand R (Anm.: Diesen zur Stromstärkemessung eingebauten Widerstand nennt man dann shunt) an, so kann man mittels Ohmschen Gesetz I = U/R sehr einfach vom Spannungsverlauf auf den Stromverlauf schließen. Im konkreten Fall verwende ich einen Widerstand R = 1 Ω, was die Sache noch einfacher macht, denn dann ist von den Werten her I gleich U. Zeigt mir das Oszilloskop also eine Spannung von z.B. 130 mV an, so fließt gerade ein Strom von 130 mA.
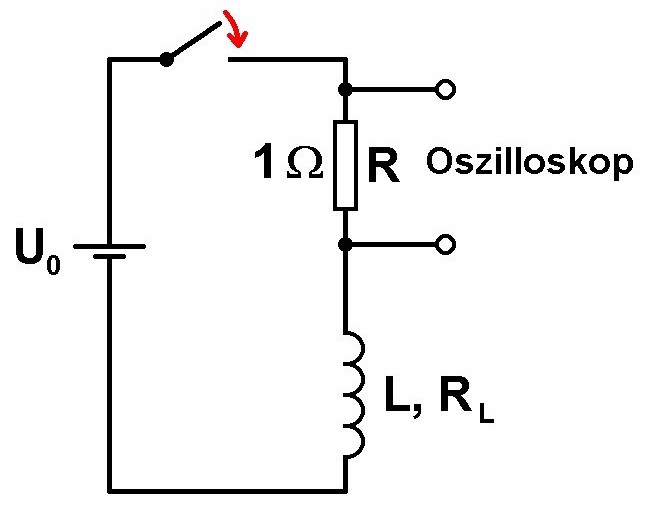
Für den Spannungsverlauf U(t) am Widerstand R gilt dann die Formel:

Die für diese Versuche verwendete Ringkerndrossel:

In der unteren Abbildung erkennt man gut, dass die Spannung U(t) sich dem Grenzwert 500 mV nähert. Dieser Grenzwert ist aber genau der Ausdruck vor der Klammer, also 0.5 = U0 · R / (R + RL). Setzt man nun konkret die Batteriespannung U0 = 1.25 V und R = 1 Ω ein, so erhält man für den restlichen ohmschen Widerstand der Schaltung RL = 1.5 Ω.
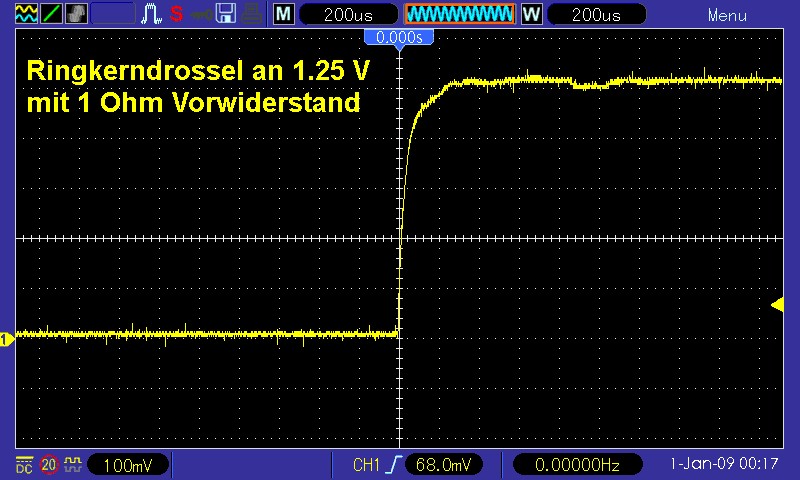
Wählt man eine kürzere Zeitbasis (20 µs) am Oszilloskop, so kann man den anfänglichen Strom- bzw. Spannungsanstieg besser erkennen:
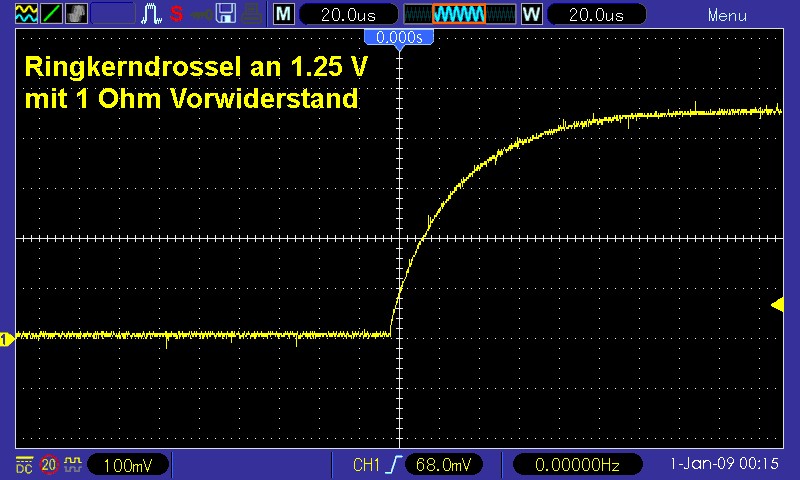
Wählen wir nun einen konkreten Punkt auf der Kurve aus und zwar U(t = 20 µs) = 0.24 V:
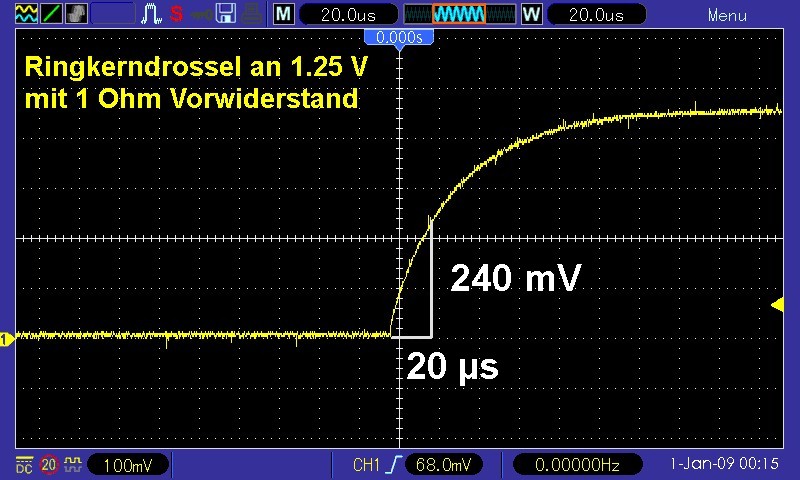
Jetzt holen wir unsere Excel-Simulation hervor und verstellen für U0 = 1.25 V, R = 1 Ω und RL = 1.5 Ω die Induktivität L solange, bis die Simulation ebenfalls U(t = 20 µs) = 0.24 V ergibt.
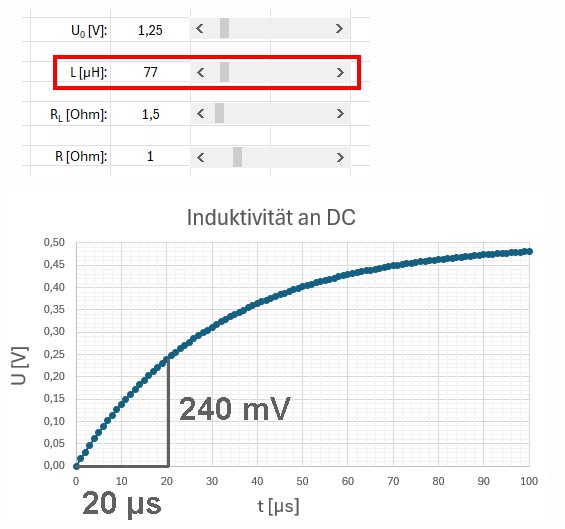
Konkret ist dies bei einer Induktiviät L = 77 µH der Fall.
Ich habe oben aber eine zweite Variante zur Bestimmung der Induktivität versprochen. Betrachten wir hierfür noch einmal die Gleichung für den zeitlichen Stromverlauf I(t):

Es gilt also U0 = L · dI/dt(t = 0), sprich Induktivität L mal dem Stromanstieg dI/dt ganz zu Beginn. Wenn wir uns jetzt die Formel U = – L · dI/dt ansehen, bemerken wir die große Ähnlichkeit. Für den Zeitpunkt unmittelbar nach Schließen des Schalters t = 0 fällt also scheinbar die gesamte Batteriespannung U0 an der Induktivität L als Selbstinduktion ab.
Möchten wir also L bestimmen, so müssen wir neben U0 noch den Stromanstieg dI/dt zum Zeitpunkt t = 0 kennen. Dieser lässt sich aber am Oszilloskopbildschirm leicht ablesen:

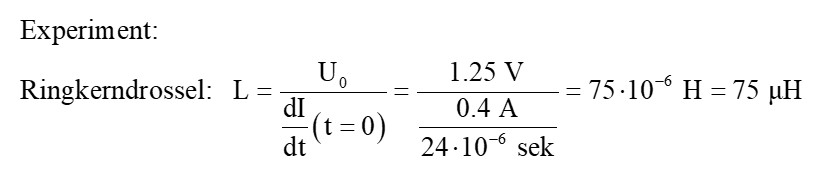
Mit dieser zweiten Methode komme ich also auf eine Induktivität L = 75 µH.
Anstelle einer Ringkerndrossel verwenden wir jetzt eine gewöhnliche Glühbirne und messen neuerlich den Stromanstieg, wenn die Glühbirne über einen Schalter und einem Vorwiderstand an eine Spannungsquelle (wieder mit U = 1.25 V) angeschlossen wird:

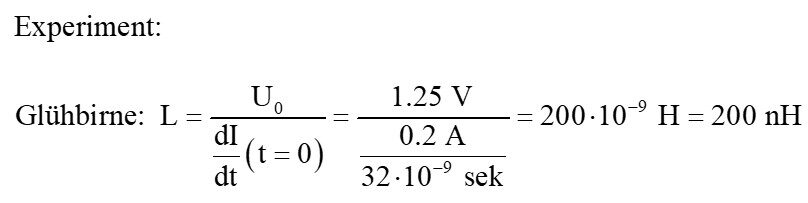
Jetzt fragt sich bestimmt der eine oder andere, was eine Glühbirne mit einer Induktivität zu tun hat? Nun, eine jede klassische Glühbirne besitzt als Herzstück eine Glühwendel und diese ist als Spule geformt. Deren Induktivität L ist aber wie wir oben berechnet haben sehr gering…


Betrachten wir bei der Glühbirne den Stromverlauf I(t) weiter, so erkennt man nach dem anfänglichen Anstieg wieder eine Abnahme der Kurve:
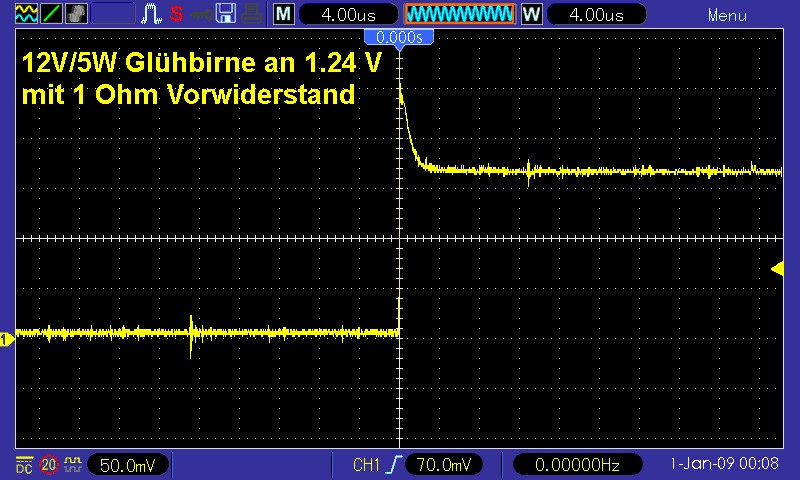
Was könnte der Grund hierfür sein? Die Glühbirne ist unmittelbar nach dem Einschalten noch kalt und daher ihr Widerstand R gering. Daher fließt zu Beginn ein höherer Strom. Binnen kurzer Zeit erwärmt sich aber die Glühwendel durch den fließenden Strom und ihr Widerstand R steigt. Die Stromstärke I nimmt dem ohmschen Gesetz I = U/R zufolge wieder ab und pendelt sich auf einen konstanten Wert ein.
In einer dritten Variante schießen wir die Spule mit der zu bestimmenden Induktivität L an eine Wechselspannung an. Bei einer Spule verläuft die Stromkurve I(t) und Spannungskurve U(t) nicht phasengleich, sondern sie besitzt eine Phasenverschiebung von 90° = π/2:
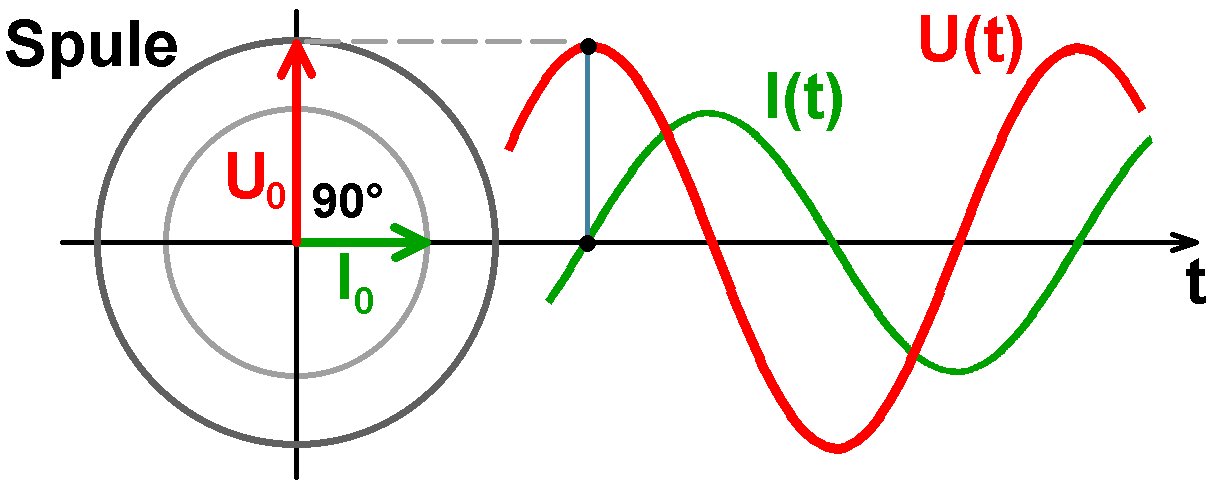
Die Spannung läuft bei einer Spule der Stromstärke voraus. Bei Wechselstrom tritt anstelle des ohmschen Gesetzes R = U/I die sog. Impedanz Z = U0 / I0 mit der Spannungsamplitude U0 und der Stromstärkeamplitude I0.

Für eine reine Spule mit der Induktivität L gilt ZL = ω · L = 2 · π · f · L.
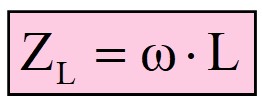
Die Impedanz einer Spule steigt also mit zunehmender Frequenz f. Dies ist auch nachvollziehbar, denn bei einer höheren Frequenz des Wechselstroms ändert sich das Spulenmagnetfeld in ihr selbst schneller und die Selbstinduktionsspannung ist größer. Diese wirkt aber der Ursache entgegen und behindert somit stärker den Stromfluss, sprich ihr Widerstand steigt. Bei Gleichspannung mit f = 0 besitzt die reine Induktivität überhaupt keinen Widerstand mehr.
Betrachten wir folgende einfache Serienschaltung aus R und L:
Für einen ohmschen Widerstand gilt ZR = U0 / I0 = R. Kennt man also die Spannungsamplitude U0 am Widerstand und seinen Wert R, so kann man die Stromamplitude I0 bestimmen. In der obigen Serienschaltung ist der Strom aber überall gleich, sprich die Stromamplitude durch die Induktivität L ist ebenfalls dasselbe I0. Kennt man nun auch noch U0 an der Spule, so kennt man demzufolge deren Wechselstromimpedanz ZL ≈ ω · L = 2 · π · f · L. Ist zudem die Wechselstromfrequenz f bekannt, kann die Induktivität L berechnet werden.
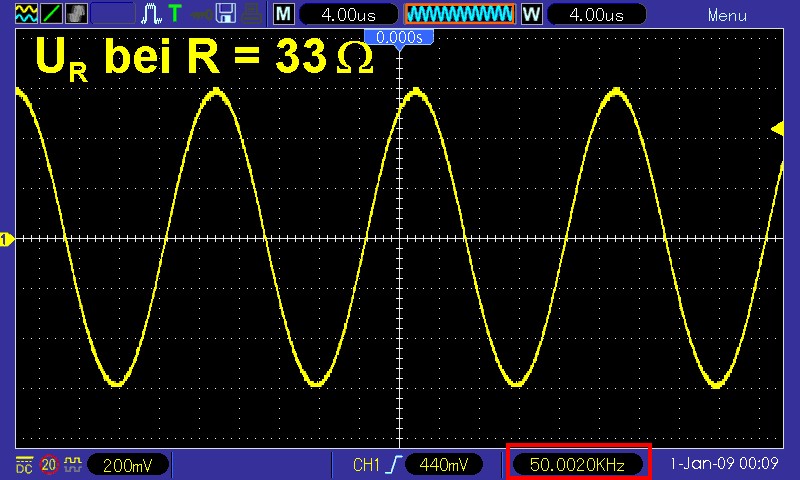
Der Spannungsverlauf U(t) am ohmschen Vorwiderstand mit R = 33 Ohm:
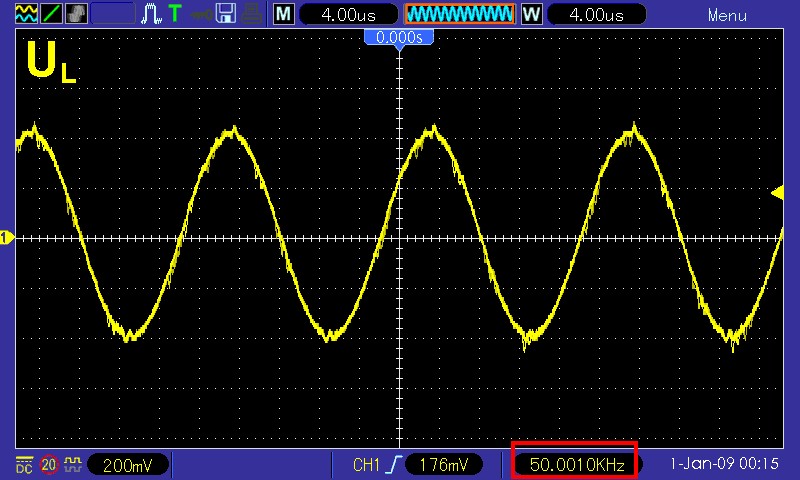
Der Spannungsverlauf an der Spule/Drossel:
Die Rechnung:

Wir erhalten abermals einen Wert um die 70 µH, Heureka 😉
Für die Induktivität L einer Spule gibt es eigene Messgeräte, sog. LCR-Meter, welche Induktivitäten L, Kapazitäten C und ohmsche Widerstände R messen können. Auf Aliexpress gibt es günstige Geräte um nicht einmal 20 Euro, mit denen die Kenngrößen von Spule und Kondensator sehr schnell und bequem ermittelt werden können. Zur Überprüfung meiner obigen Messungen habe ich die Ringkerndrossel an mein Messgerät geklemmt.
Ergebnis: L = 80 µH bzw. im anderen Modus 64 µH.




Weiter oben haben wir sogar eine Formel zur Berechnung der Induktivität einer Zylinderspule kennengelernt, in welche man die Abmessungen der Spule (Länge l, Querschnitt A) und die Anzahl n der Windungen einsetzen muss. Für eine Luftspule könnten wir so L auch sehr einfach berechnen. Im konkreten Fall liegt aber bei der Ringkerndrossel keine Luftspule vor, sondern sie ist um einen Eisenkern gewickelt. Dieser besitzt die unbekannte Permeabilität μr, quasi der Verstärkungsfaktor des Magnetfelds. Genau dieses μr wollen wir zum Schluss dieses Experiments noch ermitteln. Wir kennen n, l, A und eben L der Spule und suchen das μr:



Das Youtube-Video zum Experiment reiche ich wie immer nach…

