Viele Kinder spielen u.a. mit Autos und demzufolge besitzen sie oft auch eine Hot wheels ® Rennbahn. Mit dieser kann man auch Physik betreiben.

Quelle: Mattel – Hot wheels
Beim ersten Versuch geht es um unterschiedliche Bewegungen, konkret um eine möglichst gleichförmige Bewegung (v = konstant) bzw. um eine gleichmäßig beschleunigte (a = konstant).
Für die gleichförmige Bewegung stößt man das Auto am Beginn einer geraden, horizontalen Strecke an. Entweder stoppen Schüler die Zeit an diversen Messpunkten oder aber man verwendet wie ich eine Software zur Videoanalyse. Hier bietet sich die kostenlose Software Tracker (https://physlets.org/tracker/) an.

Zur Videoanalyse benötigt man auch die konkreten Abmessungen zum Kalibrieren des Videos:


Das kurze Video:
Mit Tracker kann man sich dann verschiedene Diagramme (s(t), v(t), a(t) usw.) anzeigen lassen:
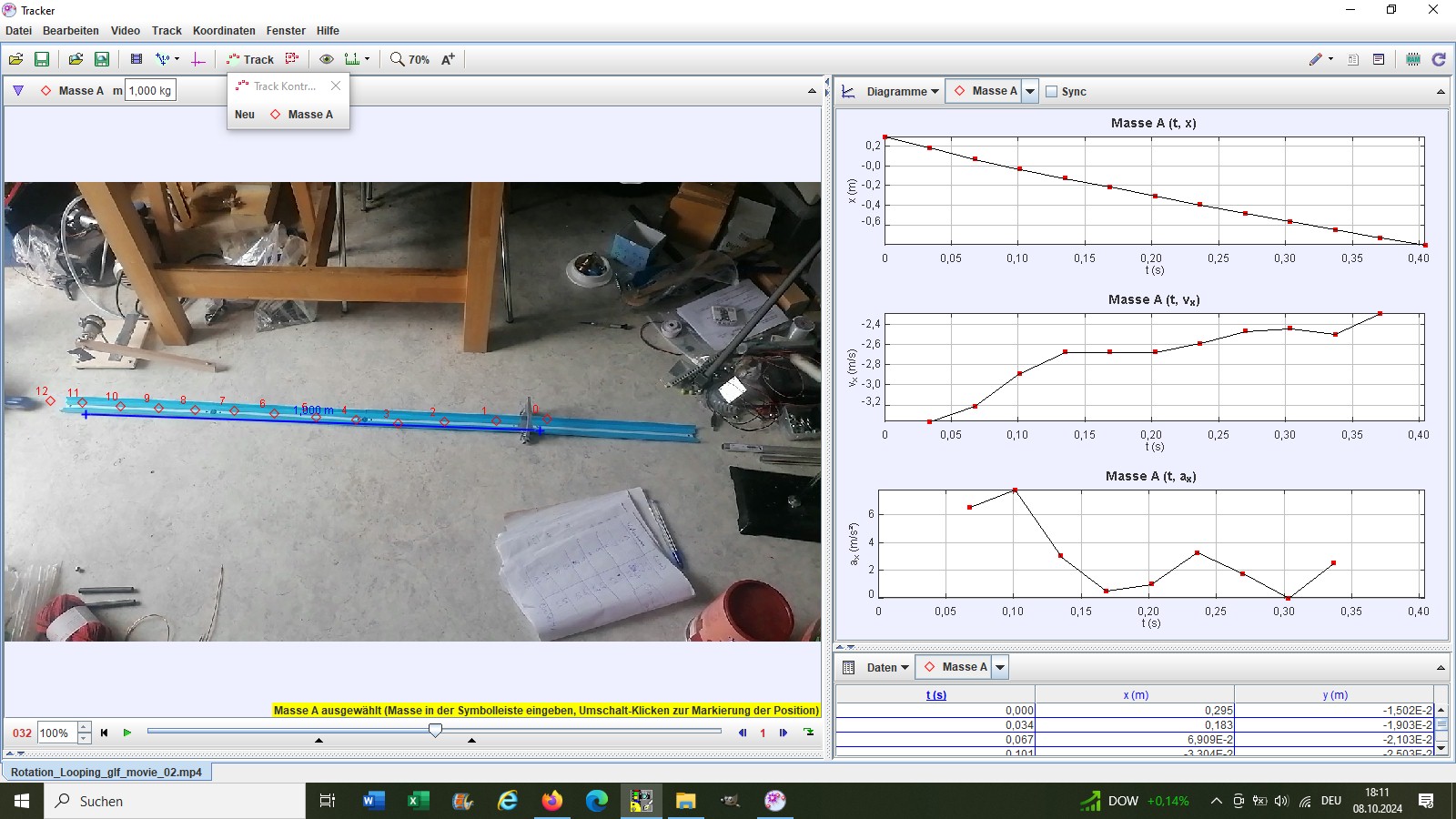
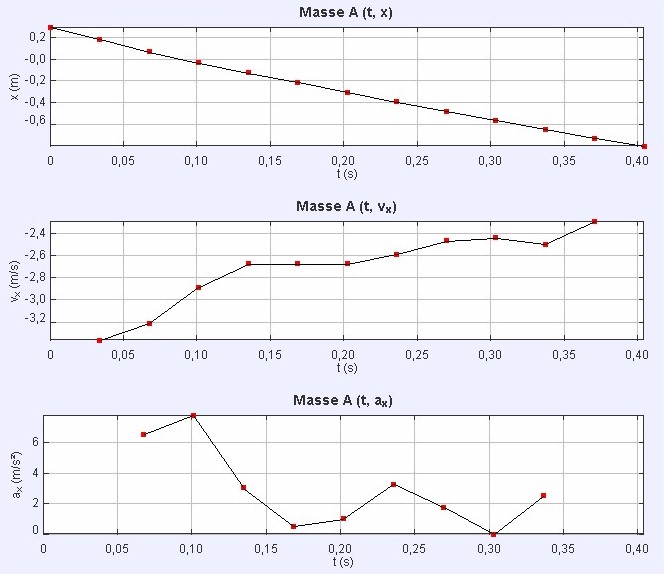
Wie man im zweiten Diagramm oben sieht, ist die Geschwindigkeit des Autos nicht wirklich konstant sondern nimmt während der Fahrt aufgrund der Reibung ab.
Bei einer gleichförmigen Bewegung sollten die Diagramme wiefolgt aussehen:

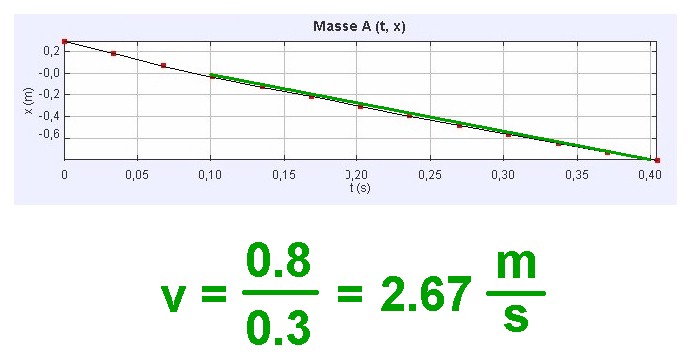
Hier das experimentell erhaltene s(t)-Diagramm, aus dem sich über die Steigung die (konstante) Geschwindigkeit v ermitteln lässt. Konkret waren es v = 2.67 m/s.
Für die gleichmäßig beschleunigte Bewegung muss man mit der Rennbahn eine schiefe Ebene aufbauen:

Deren Abmessungen (z.B. Länge der Fahrbahn, Höhenunterschied) benötigt man dann später wieder für die Kalibrierung der Videoanalyse:

Die Höhe betrug konkret 42 cm…

und die Länge der Rennstrecke (Hypothenuse) 139 cm:

Zum Einsatz kam das Lieblingsauto meines jüngsten Sohns, ein Subaru Impreza wrx sti Ralleyauto:

Das kurze Video:
Die Auswertung mit der Software Tracker:
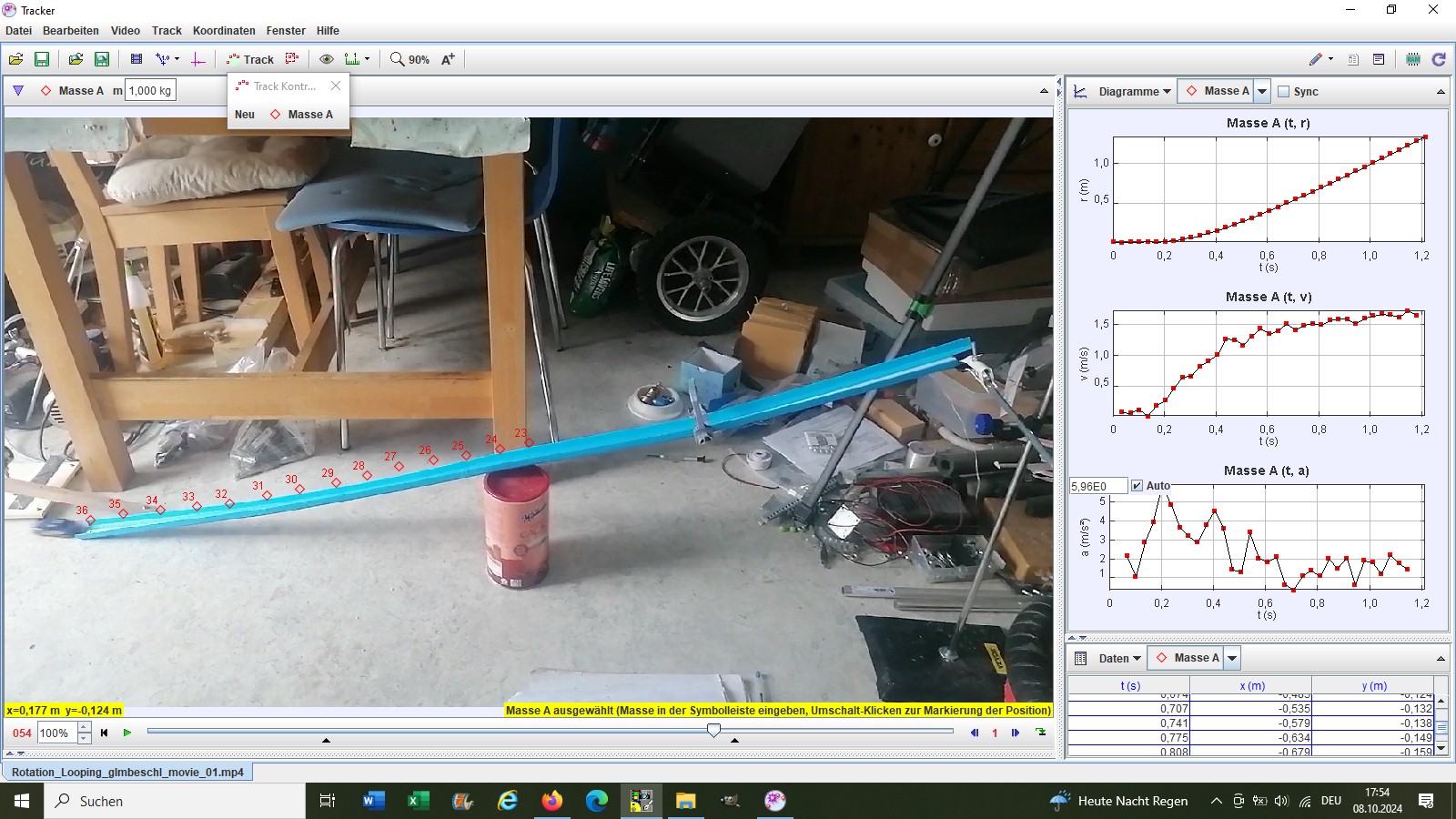
Die s(t), v(t) und a(t)-Diagramme:

Im Idealfall sollten diese bei einer gleichmäßig beschleunigten Bewegung wiefolgt aussehen:
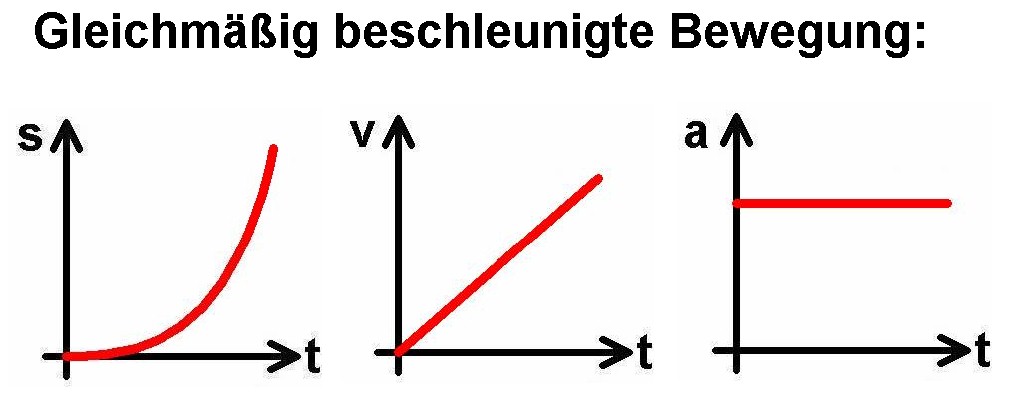
Aus der Steigung des v(t)-Diagramms erhält man die Beschleunigung a:

Theoretisch sollte sich eine Beschleunigung von a = 2.97 m/s² ergeben.

Meine experimentell erhaltene Beschleunigung liegt mit a = 3.125 m/s² sogar darüber. Grund wird die Durchbiegung der Strecke sein, sodass sich zu Beginn ein stärkeres Gefälle und damit einer höhere Beschleunigung ergeben hat.
Besitzt die Rennbahn einen Looping, kann man noch ein weiteres Experiment durchführen. Und zwar geht es darum diejenige Höhe h zu ermitteln, ab der das Auto einen am Boden befindlichen Looping mit dem Radius r vollständig durchfahren kann, ohne den Kontakt zur Bahn zu verlieren.
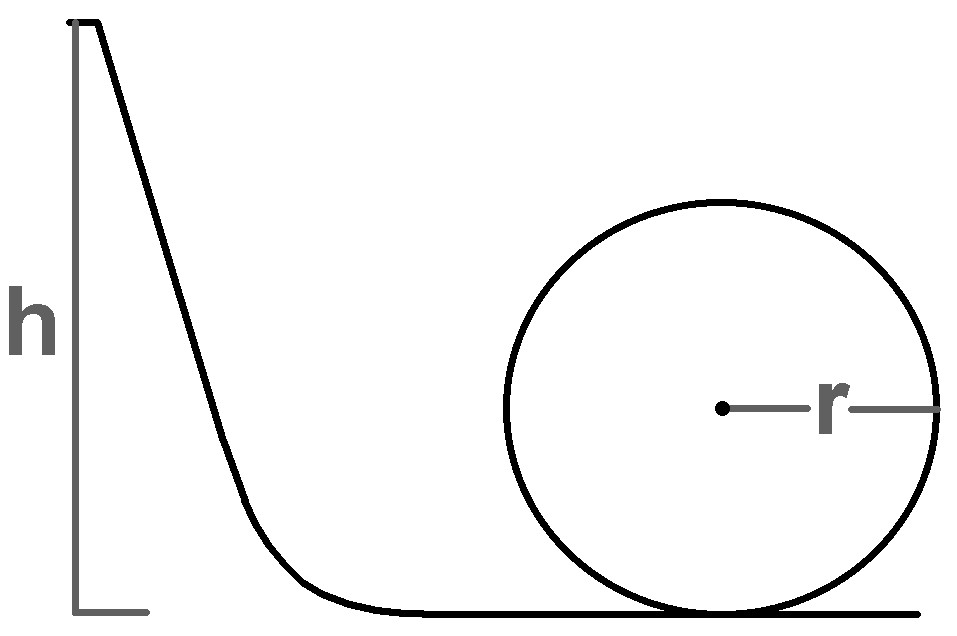


Mittels eines Laborstativs stellte ich unterschiedliche Starthöhen h ein:

Der Radius des Loopings betrug konkret r = 11.5 cm.

Damit Reibungseffekte eine geringere Rolle spielen, verwendete ich für diesen Versuch anstatt des Modellautos eine Metallkugel:


Hier zwei kurze Videos für unterschiedliche Höhen und zwar h = 57 cm …
… bzw. h = 41 cm:
Ohne Reibung lässt sich die minimale Starthöhe h für einen vollständigen Looping auch berechnen:

Den konkreten Wert für r = 11.5 cm eingesetzt ergibt sich daraus:
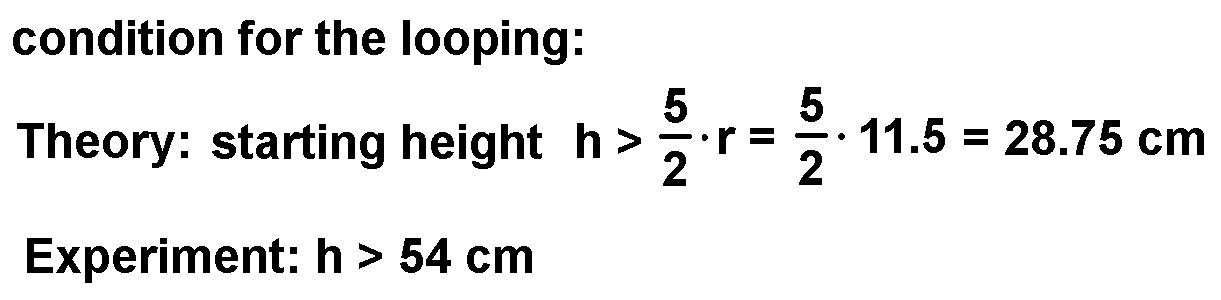
Der Unterschied zwischen Theorie und Experiment ist beachtlich. Demnach verliert auch scheinbar die Metallkugel durch Reibung und Rotation massiv an Energie 😉
Das Youtube-Video reiche ich wie immer nach…

