Aus dem Bereich der Mechanik gibt es einen schönen Versuch und zwar das sog. Maxellrad. Dabei handelt es sich um ein Metallrad mit dünner Achse (kleiner Radius r) mit möglichst großem Trägheitsmoment I. Es wird mit zwei Fäden aufgehängt und diese zunächst um die Achse aufgewickelt. Dann lässt man das Maxwellrad los und es bewegt sich langsam nach unten und wieder hoch.
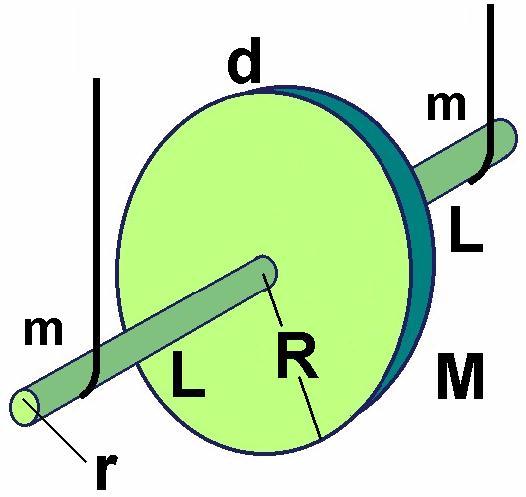
Dabei kann man schön den Energieerhaltungssatz beobachten. Konkret wechselt sich potentielle Energie mit kinetischer und Rotationsenergie ab. Die langsame Bewegung kann man über das wirkende Drehmoment T erklären. Durch den geringen Radius r der Achse wirkt nur ein geringes Drehmoment T. Das Trägheitsmoment I ist aber sehr groß. Gemäß der Formel T = I · α bewirkt nun ein kleines Drehmoment T bei einem großen Trägheitsmoment I eine sehr geringe Winkelbeschleunigung α.

Ich habe die Beschleunigung a nach unten auf zwei verschiedene Arten hergeleitet, einmal über den Energieerhaltungssatz und dann mittels der Gleichung T = I·α.
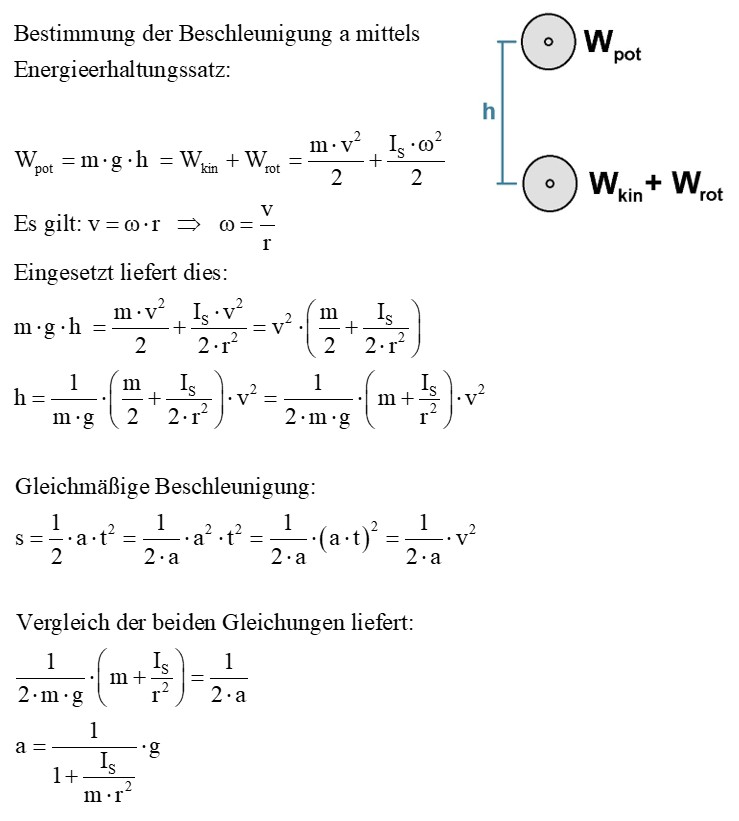
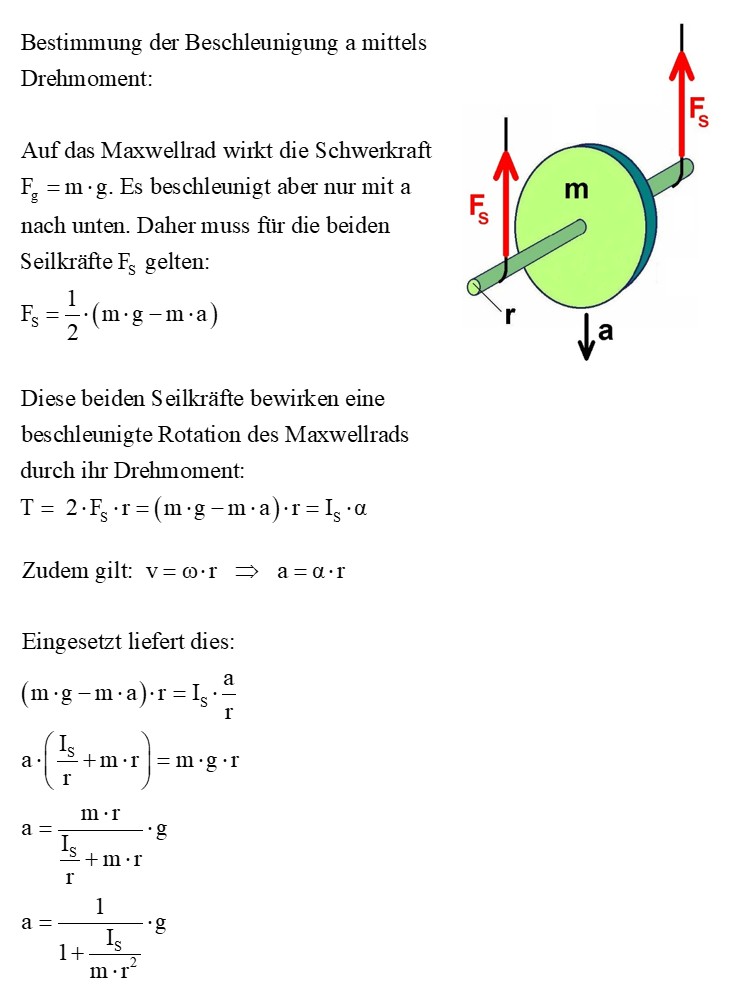
Durch das große IS im Verhältnis zu m·r² kommt es also zu einer deutlich reduzierten Beschleunigung a << g nach unten.
Auf der österreichischen Verkaufsplattform willhaben.at bin ich auf ein solches Maxwellrad gestoßen, welches ich dann auch gekauft habe.
Das gebrauchte Maxwellrad ist wohlbehalten bei mir angekommen und so konnte ich es gleich testen…





Mittels der Gesamtmasse m = 530 g und den Abmessungen konnte ich das Trägheitsmoment IS des Rotationskörpers berechnen:
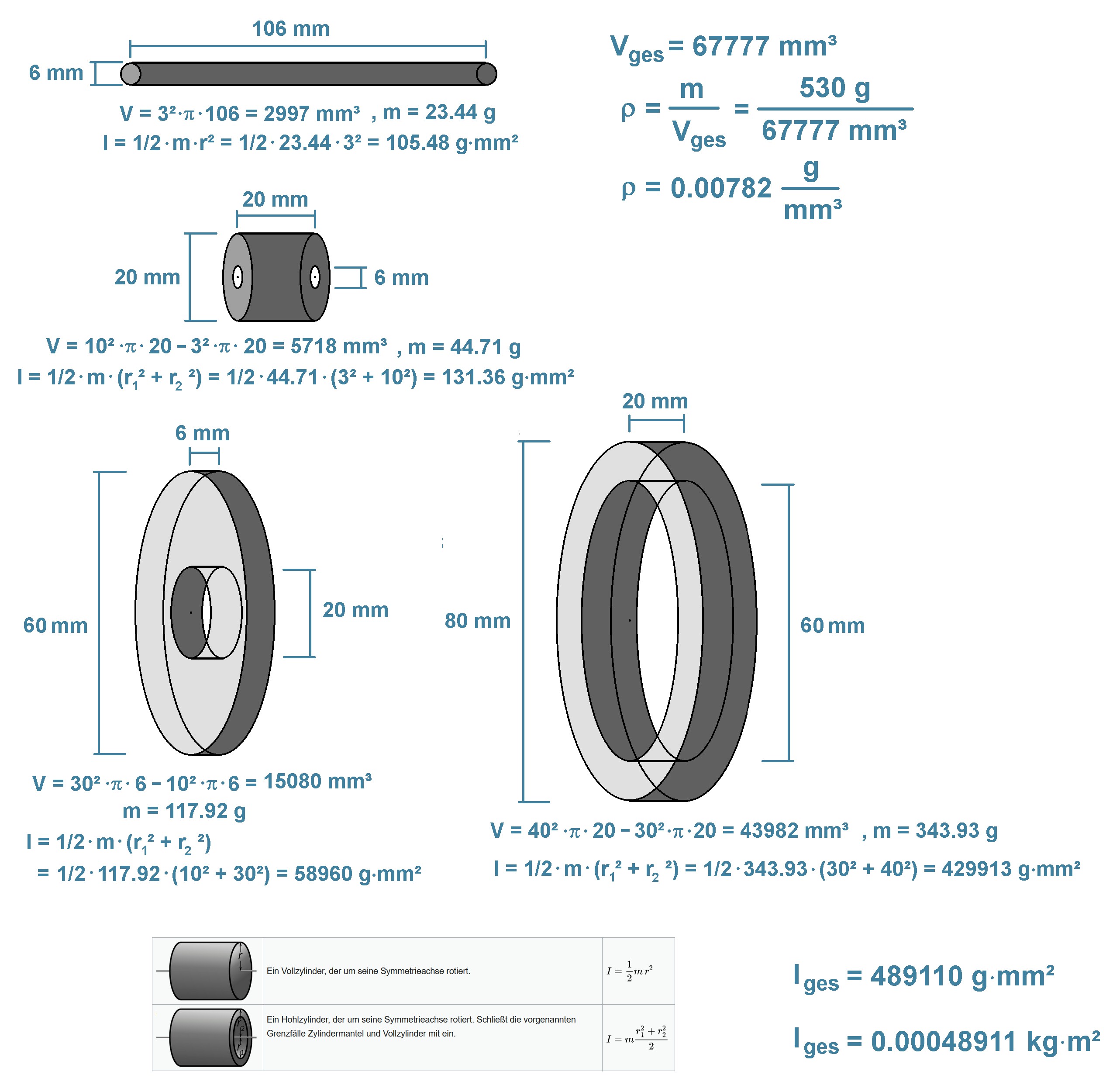
Ich komme auf ein Trägheitsmoment IS = 0.00049 kg·m². Dies gilt es nun experimentell mittels der Beschleunigung a zu bestätigen:

Zur Videoanalyse verwende ich die Software „Tracker“:
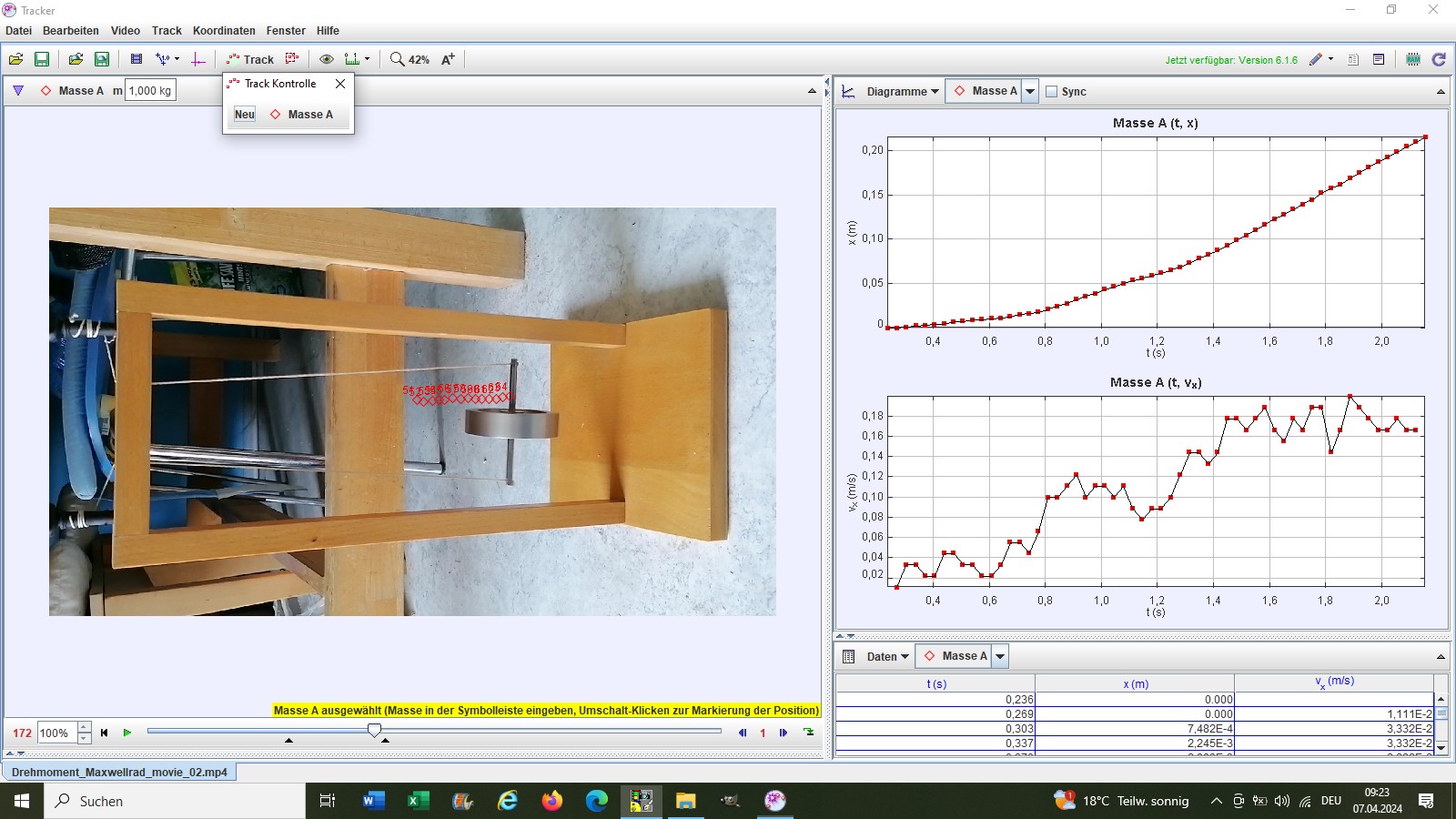

Mit dieser konnte die Beschleunigung zu a = 0.1071 m/s² bestimmt werden. Eingesetzt in die Formel für a liefert dies das gesuchte Trägheitsmoment:

Der Unterschied zwischen Theorie und Experiment hält sich in Grenzen, Heureka… 😉

