Bildquelle: https://de.wikipedia.org/wiki/Datei:Broglie_Big.jpg
Auf den berühmten französischen Physiker Louis de Broglie (1892-1987) geht eine einfache, unscheinbare physikalische Beziehung zurück, welche aber weitreichende Folgen hat. Sie verknüpft den Impuls p mit der Wellenlänge λ wiefolgt:
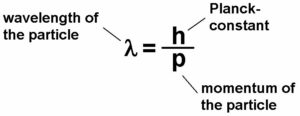
Für seine Arbeiten auf dem Gebiet der Materiewellen erhielt de Broglie 1929 den Nobelpreis in Physik. Welche Aussagen können mittels obiger Gleichung gemacht werden?
Besitzt ein Teilchen etwa einen Impuls p = m·v, so besitzt es scheinbar auch eine Wellenlänge λ und zwar je größer p, desto kleiner wird λ. Ein Teilchen hat also auch Welleneigenschaften.
Umgekehrt besitzt eine Welle wie etwa Licht eine bestimmte Wellenlänge, so hat diese auch einen Impuls p und zwar je kleiner die Wellenlänge, desto größer der Impuls. Klassisch betrachtet konnte dies nicht sein, da etwa ein Lichtteilchen (Photon) die Masse 0 besitzt und demnach dessen Impuls p = m·v auch 0 sein müsste.
Wie kann man nun diesen fundamentalen Zusammenhang einer typischen Welleneigenschaft mit einer typischen Teilcheneigenschaft experimentell beweisen?
Nehmen wir beschleunigte Elektronen. Diese besitzen durch ihren Impuls p = m·v scheinbar auch eine Wellenlänge λ. Durch die geringe Größe des Planckschen Wirkungsquantums h = 6.63·10^ –34 Js wird diese auch in der Regel sehr klein sein (trotz des auch sehr kleinen Impulses). Und in der Tat, schnelle Elektronen verhalten sich wie Licht geringer Wellenlänge. Umgesetzt wird dies eindrucksvoll in Form des Elektronenmikroskops. Es ist dem optischen Mikroskop sogar weit überlegen, da seine Auflösung durch die weitaus geringere Beugung (Anm.: Beugungserscheinungen werden ja mit schrumpfender Wellenlänge kleiner) ungleich höher ist. Dies ist auch der Grund, warum mit einem Elektronenmikroskop überhaupt so dermaßen hohe Vergrößerungen erzielt werden können. Bei einem optischen Mikroskop ist hingegen bereits bei ca. 1000-facher Vergrößerung das obere Limit erreicht.
Eine kleine Rechnung dazu: Nehmen wir an, die Elektronen werden durch eine Spannung von 4 kV beschleunigt. Dann gilt:

Bei 4 kV Beschleunigungsspannung besitzt also das Elektron eine um den Faktor 30000 kleinere Wellenlänge!
Obwohl es sogar Amateure gibt, welche sich ihr eigenen Elektronenmikroskop gebaut haben, ist ein derartiges Vorhaben wohl für die meisten nicht umsetzbar. Es gibt aber eine einfachere und günstigere Variante, die Wellennatur von bewegten Teilchen zu beweisen und zwar mittels einer Elektronenbeugungsröhre.
Eine solche Röhre besteht aus einem evakuierten Glaskolben, indem Elektronen mit Hochspannung (ca. 1 bis 5 kV) beschleunigt werden. Sie treffen auf ein mit Graphitpulver belegtes Trägernetz. Die einzelnen Graphit“kristalle“ besitzen eine regelmäßige Anordung der Kohlenstoffatome (Gitterstruktur), wobei sich Ebenen/Schichten mit einem bestimmten Abstand d bilden. An diesen Ebenen werden nun die Materiewellen nur unter ganz bestimmten Bedingungen (sog. Bragg-Gleichung) reflektiert. Diese Bragg-Gleichung drückt die Bedingung für konstruktive Interferenz aus und lautet:
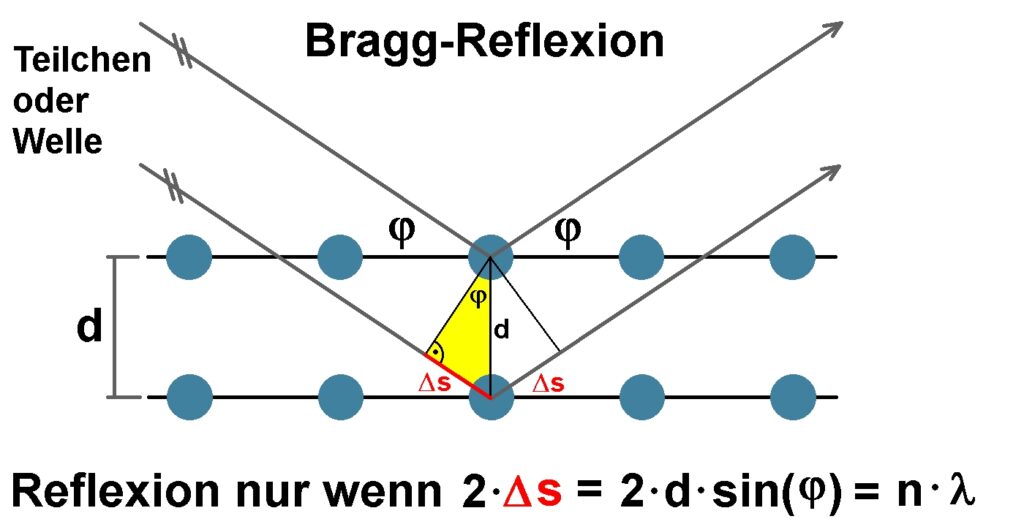
Die gleichartigen Graphitkristalle besitzen alle einen bestimmten Gitterabstand d und die beschleunigten Elektronen alle eine bestimmte Wellenlänge λ. Demnach kommt es nur bei einem ganz bestimmten Einfallswinkel φ zur Reflexion. Hätte man einen Einkristall aus Graphit, so wäre es reiner Zufall, dass die Elektronen auch genau unter diesem Winkel auf die Gitterebene eintreffen. Da es sich aber um Graphitpulver handelt und demnach die einzelnen Kristalle völlig regellos angeordnet sind, gibt es immer einige genau richtig ausgerichtete Gitterebenen/Kristalle. Da dieser Effekt rotationssymmetrisch ist, entsteht kein einzelnes Beugungsmaximum, sondern ein Beugungsring.
Graphit besitzt zwei dominante Gitterabstände und zwar d10 = 0.213 nm bzw. d11 = 0.123 nm. Demnach müssten sich 2 Beugungsringe auf dem Phosphorschirm abzeichnen, was auch der Fall ist. Der äußere Beugungsring (größeres φ) gehört dabei zum kleineren Gitterabstand d11.
Welchen Einfluss hat nun die Beschleunigungsspannung U auf die Beugungsringe? Nun, erhöhen wir die Spannung U, so werden die Elektronen stärker beschleunigt und ihre Geschwindigkeit v bzw. ihr Impuls p wächst. Ein größerer Impuls p hat aber nach der Formel von de Broglie eine kleinere Wellenlänge zufolge. Und eine kleinere Wellenlänge λ bedingt laut Bragg-Gleichung bei gleichem Gitterabstand d einen kleineren Reflexions/Beugungswinkel φ. Mit zunehmender Spannung müssten die Beugungsringe also schrumpfen. Auch das zeigt sich im Experiment.

Möchte man nun die Wellenlänge der beschleunigten Elektronen experimentell bestimmen, so muss man zunächst den Radius r der Beugungsringe abmessen. Im gelb markierten, rechtwinkligen Dreieck gilt dann folgende Beziehung: tan(2·φ) = r/x bzw. nach φ aufgelöst: φ = 1/2 · arctan(r/x).
Diesen Winkel φ und den bekannten Gitterabstand d setzt man nun in die Bragg-Gleichung sin(φ) = 1·λ / (2·d) und berechnet daraus die Wellenlänge λ. Das Ergebnis müsste sich mit jenem auf Basis der de Broglie-Beziehung decken.

Wie man am Ergebnis sieht, decken sich der experimentell bzw. theoretisch ermittelte Wert ausgezeichnet!
Zum experimentellen Aufbau: Beugungsröhren sind nicht gerade billig (ca. 500 Euro). Ich konnte durch Zufall über ebay.kleinanzeigen günstig (136 Euro) an eine solche vom Typ Leybold 555 17 kommen. Neben der Röhre wird noch ein Hochspannungsnetzteil (0-5 kV) benötigt. Dieses habe ich wie so oft bei meinen Experimenten mit einem CCFL-Inverter plus nachgeschalteter 2-stufiger Kaskade umgesetzt.
Zur Anzeige der Hochspannung dient ein 0-2 kV Panelmeter. Damit es durch die höhere Beschleunigungsspannung nicht zerstört wird, erhält es einen 180 MOhm Vorwiderstand. Bei einem Innenwiderstand von 20 MOhm zeigt es also genau 1/10 der tatsächlichen Spannung an.
Die Heizung des Beugungsröhre betreibe ich mit einem 6V/3W Trafo, wobei die Stromstärke mit einem 10 Ohm-Potentiometer reguliert wird. Der maximal zulässige Heizstrom beträgt nämlich 300 mA. Auch darf die Beschleunigungsspannung 5 kV und der Anodenstrom 200 µA nicht überschreiten. Zu diesem Zweck habe ich entsprechende Anzeigen bei meinem Aufbau installiert.