Ein Kugelpendel besteht aus einem sphärischen Hohlspiegel, indem eine Kugel aufgrund der Schwerkraft Schwingungen vollführt. Auf diese Weise lässt sich sogar die Brennweite f des Spiegels mit einer Stoppuhr bestimmen. Hierfür muss man zunächst die Formel für die Periodendauer der Schwingung herleiten:

Die rücktreibende Kraft F(x) ist direkt proportional zur Auslenkung x:


Den Hohlspiegel mit möglichst geringer Brennweite habe ich auf ebay.com entdeckt:


Die Periodendauer konnte ich experimentell zu τ = 1.157 sek bestimmen:

Damit lässt sich der Krümmungsradius R des Hohlspiegels ermitteln:

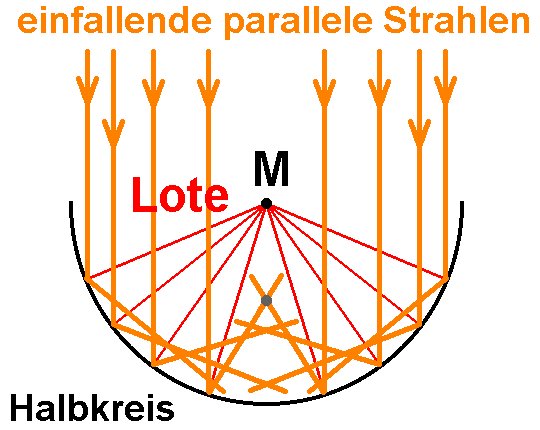
Wie gelangt man nun aber von R zur Brennweite f? Betrachten wir hierzu einen Strahlengang genauer:


Wie man anhand der Herleitung erkennen kann, gilt die Beziehung f = R/2 nur für achsnahe Strahlen. Treffen diese weiter vom Zentrum entfernt auf den Spiegel, so liegt deren Brennpunkt näher beim Spiegel. Ein Kugelspiegel besitzt also keinen gemeinsamen Brennpunkt. Da dies einen optischen Abbildungsfehler verursacht spricht man auch von sphärischer Aberration (https://de.wikipedia.org/wiki/Abbildungsfehler).
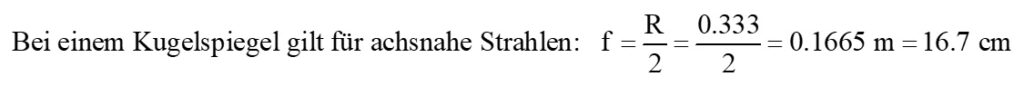
Die Brennweite des Hohlspiegels lässt sich natürlich auch optisch z.B. mittels zweier parallel ausgerichteter Laserpointer bestimmen. Der Abstand des Kreuzungspunkts zur Spiegeloberfläche entspricht dann der Brennweite f.





Papier unterhalb des Brennpunkts:

Papier in der Brennebene:

Papier oberhalb des Brennpunkts:

Auf diese Weise erhielt ich für die Brennweite einen Wert von rund 13 cm. Dieses Ergebnis deckt sich einigermaßen mit jenem ermittelt mittels Schwingungsdauer. Der Grund der Abweichung dürfte u.a. darin liegen, dass erstens die Reibung die Periodendauer τ der Kugel erhöht (dies würde dann eine zu große Brennweite ergeben mittels der Kugelmethode) und zweitens sich die randnahen Laserstrahlen bei einem Abstand < Brennweite f schneiden (dies würde eine zu kleine Brennweite ergeben mittels der Lasermethode).
Zum Schluss wie immer das Youtube-Video:

