Im Zusammenhang mit dem Gasgesetz p·V = n·kB·T = ν·R·T unterscheidet man folgende Zustandsänderungen: Isotherm (T = konstant), Isobar (p = konstant) und isochor (V = konstant). Für den isothermen Fall folgt dann aus dem Gasgesetz p·V = konstant.

Halbiert man das Gasvolumen, so steigt bei gleicher Temperatur der Druck auf das Doppelte an. Beim Zusammendrücken des Kolbens leistet man aber Arbeit W = –p·dV. Dies resultiert eigentlich in einer Erhöhung der inneren Energie U des Gases, also in einer Temperturerhöhung. Die vom komprimierten Kolben reflektierten Gasteilchen besitzen augenscheinlich eine höhere Geschwindigkeit/Temperatur als vor der Reflexion.
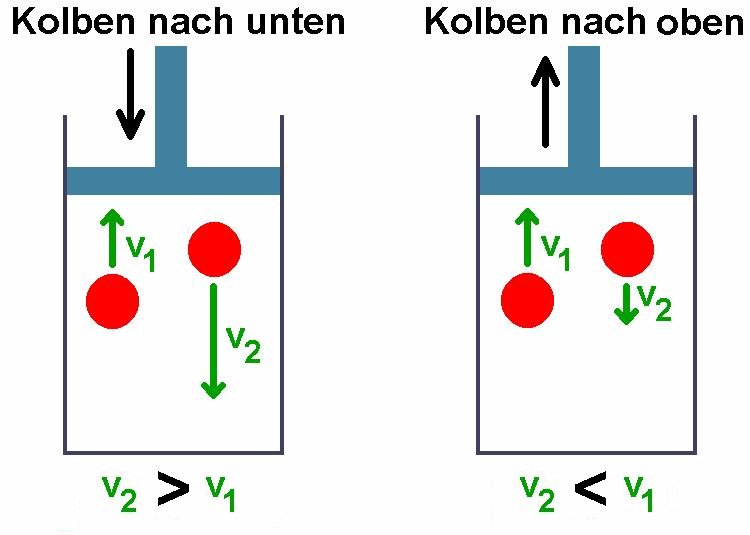
Mit einer Spritze, welche man schnell zusammendrückt, und einem Temperatursensor lässt sich diese Temperaturerhöhung experimentell nachweisen:

Damit also beim Komprimieren des Gasvolumens die Temperatur T konstant bleibt, muss diese langsam erfolgen. Dadurch hat das Gas die Möglichkeit zum Temperaturaustausch mit seiner Umgebung. Komprimiert aber das Gas sehr schnell, so kann innerhalb dieser kurzen Zeit keine Wärme Q zum Ausgleich fließen und die Temperatur steigt an. Diesen Fall Q = 0 nennt man adiabatisch.

Durch diese Temperaturerhöhung beim Komprimieren steigt der Druck also nicht nur wegen der Verkleinerung des Volumens, sondern auch wegen der T-Erhöhung. Die angepasste Gleichung lautet also für den adiabatischen Fall nicht p·V = konstant, sondern p·V^κ = konstant. Die Größe κ nennt man den Adiabatenkoeffizient. Dieser hängt von der Anzahl der Freiheitsgrade f des Gases wie folgt ab: κ = (f + 2)/f. Ein einatomiges Gas wie etwa Helium mit f = 3 sollte demnach einen Adiabatenkoeffizient von κ = 5/3 besitzen, ein zweiatomiges wie etwa N2 mit f = 5 demzufolge κ = 1.4.
Diese Temperaturerhöhung bei der Kompression kann sogar soweit gehen, dass sich im Kolben befindliche Watte von selbst entzündet:



Wie lassen sich aber nun die Adiabatengleichungen (z.B. p·V^κ = konstant) herleiten?

Der Adiabatenkoeffizient κ lässt sich auf folgende zwei Arten relativ einfach bestimmen.
1.) Methode nach Rüchardt
Für diese Methode benötigt man ein großes Glasgefäß mit einem im Stopfen befindlichen Glasrohr. In diesem Rohr befindet sich ein Schwingkörper. Lässt man diesen am oberen Ende des Glasrohrs los, so vollführt er Schwingungen. Aus der Periodendauer τ dieser Schwingung lässt sich der Adiabatenkoeffizient ermitteln…
Das Experiment kann auch im Schulmittelhandel zum Beispiel bei der Firma Leybold erworben werden: https://www.leybold-shop.de/physik/versuche-sek-ii-universitaet/kalorik/kinetische-gastheorie/spezifische-waerme-von-gasen/bestimmung-des-adiabatenexponenten-c-sub-p-sub-c-sub-v-sub-der-luft-nach-ruechardt/vp2-5-3-1.html
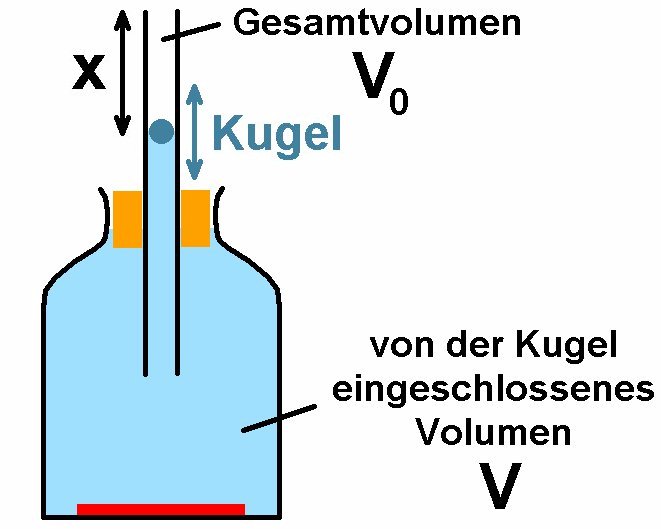
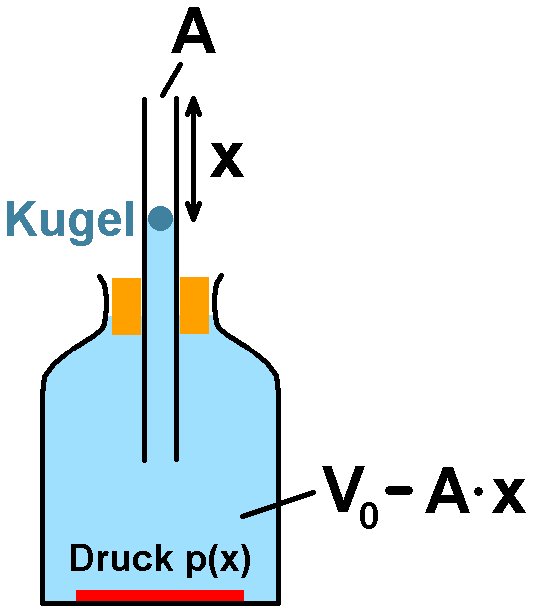
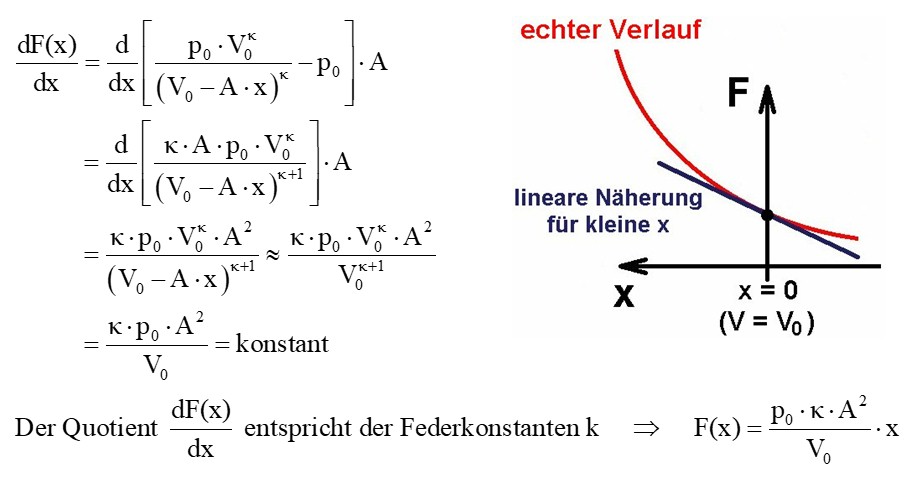
Hier die kurze Herleitung:
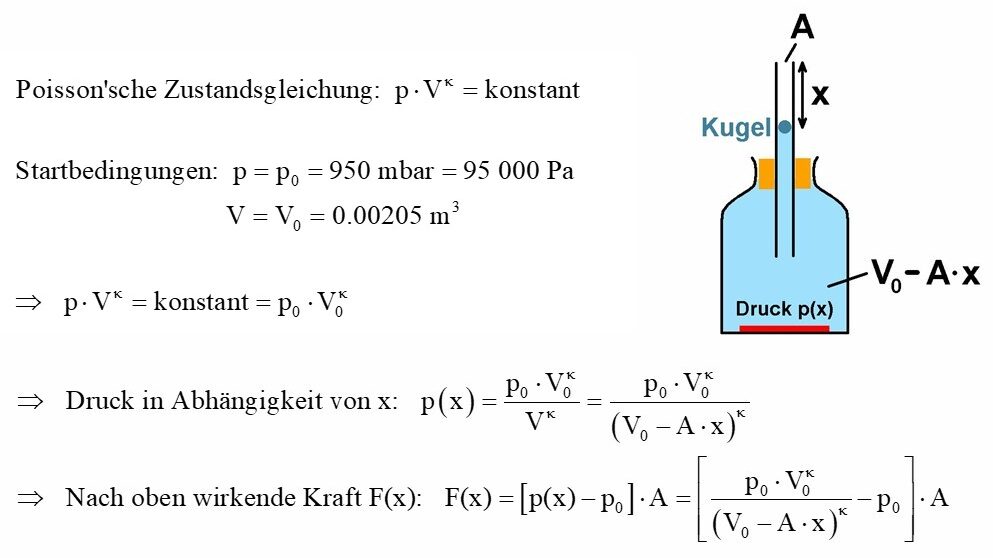

Im Schulmittelhandel kostet dieser Versuch stolze 1000 Euro. Wie immer versuche ich mich an einer möglichst einfachen und günstigen Umsetzung. Die für diesen Versuch benötigte, große Glasflasche habe ich gebraucht über http://www.willhaben.at gekauft:

Die 5 Liter Apothekenflasche:

Jene mit nur 2 l Volumen:

Ein passendes Glasrohr entdeckte ich im Computergeschäft und zwar von Alphacool (40 cm Länge, 11 mm Innendurchmesser):

Der Schwingkörper muss extrem saugend in das Glasrohr passen, da er ja das Luftvolumen in der Glasflasche dicht einschließen muss. Da ich über keine Drehmaschine verfüge, musste ich mir etwas anderes einfallen lassen. Zum Glück gibt es Bohrer in 1/10 mm Abstufung zu kaufen. Daher orderte ich auf aliexpress 3 Bohrer mit 10.9 mm, 11.0 mm und 11.1 mm Durchmesser:




Während der 11.1 mm Bohrer zu dick war, passte der 11.0 mm Bohrer exakt ins Glasrohr:


Dieser musste dann nur noch mit der Säge abgelängt werden…

Gummistöpsel hatte ich noch zuhause liegen:




Der fertige Aufbau, wobei ich in die Glasflasche zu deren Schutz noch eine Schaumstoffauflage gegeben habe:

Die Masse des Schwingungskörpers beträgt 10.753 g:


Die Durchführung des Experiments war dann nicht ganz so einfach, denn das Bohrerstück schwingte nur widerwillig im Glasrohr. Aber ich konnte zumindest eine halbe Schwingung per Kamera aufzeichnen:
Die halbe Periodendauer betrug demnach τ/2 = 0.43 sek. Dies eingesetzt in die Formel für κ ergab dann schließlich folgenden Wert für den Adiabatenexponenten:
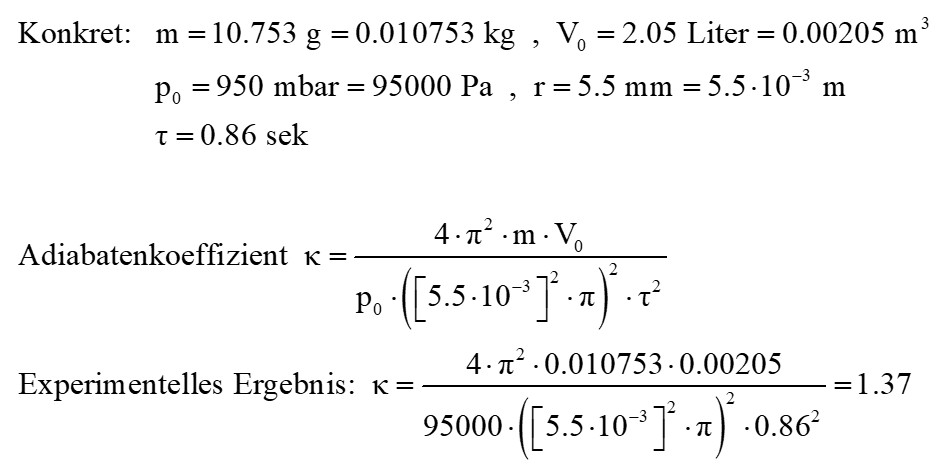
Der theoretische Wert für Luft bei 20°C beträgt 1.40. Mit der geringen Abweichung vom Sollwert bin ich eigentlich sehr zufrieden.
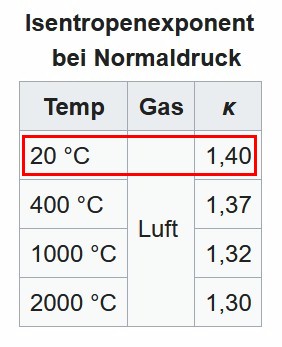
Quelle: Wikipedia
Gekostet hat mich dieses Experiment rund 50 Euro, verglichen mit den Handelspreisen (ca. 1000 Euro) ein richtiges Schnäppchen 😉
2.) Methode nach Clement-Desormes
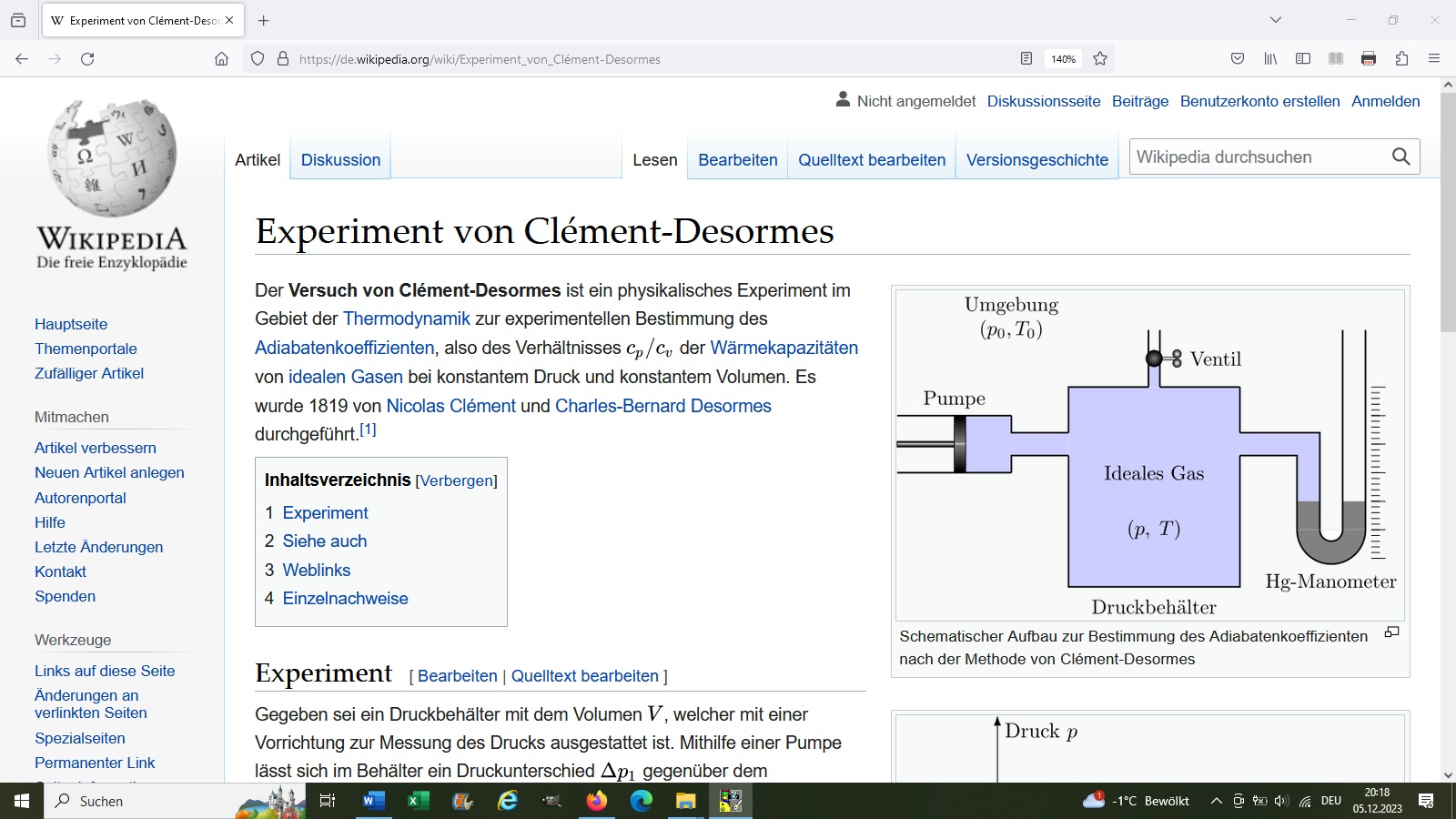
Quelle: Wikipedia
Bei dieser Methode wird zunächst ein Gefäß mit einer Fahrradpumpe auf einen Überdruck Δp1 aufgepumpt. Dabei steigt durch die adiabatische Kompression zunächst auch die Temperatur T an. Deshalb muss man nun eine Zeit lang warten, bis die im Gefäß befindliche Luft wieder Raumtemperatur besitzt. Danach lässt man über ein Fahrradventil den Überdruck adiabatisch entweichen mit der Konsequenz, dass die Luft im Gefäß nun eine geringere Temperatur besitzt. Jetzt verschließt man schnell das Ventil und wartet bei konstantem Volumen (isochor), bis die Luft wieder Raumtemperatur besitzt. Dadurch steigt der Innendruck um Δp2 an.

Ausgangspunkt bildet die Adiabatengleichung mit der Temperatur T und dem Druck p:


Setzt man diese beiden Bedingungen in die Adiabatengleichung ein, erhält man:

Für die im Anschluss isochore Zustandsänderung bedienen wir uns des Gasgesetzes:
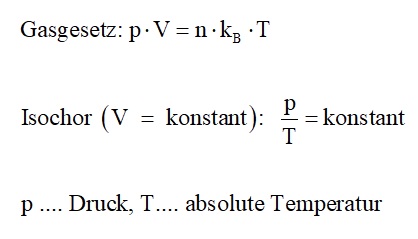

Diese Bedingungen in die isochore Gleichung p/T = konstant eingesetzt liefert:
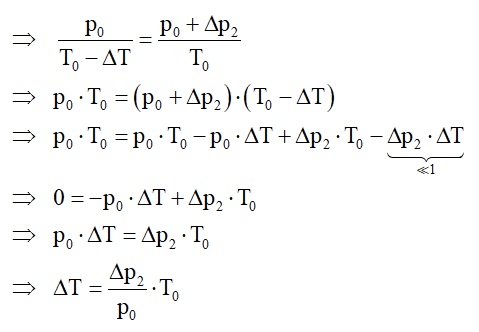
Den Ausdruck für ΔT setzt man in die obere Gleichung mit Δp1 ein:

Der Adiabatenkoeffizient lässt sich also rein nur mit den beiden Überdrücken Δp1 und Δp2 bestimmen.

Die Drücke ermittle ich mit dem Drucksensor MPRLS, welchen ich günstig auf Amazon gekauft habe. Er misst den Absolutdruck zwischen 0 und ca. 1.7 bar, was für meine Bedürfnisse ideal ist. Die Auswertung übernimmt wie so oft ein Arduino Nano:



Die Fahrradpumpe habe ich auch auf Amazon entdeckt und als Glasgefäß probiere ich es mit einem Nutellaglas. Das Ventil stammt von einem Fahrradschlauch:






Da ich das Nutella-Glasgefäß nicht vollständig dicht bekam, wechselte ich auf eine 1.5 Liter Getränkeflasche und klebte das Fahrradventil am Deckel und den Schlauchstutzen an der Seite ein.



Das Experiment verlief aber nur bedingt erfolgreich. Die adiabatische Expansion erfolgte durch das dünne Fahrradventil wohl nicht schnell genug. Daher erhöhte sich der Druck nach dem Wiederverschließen des Ventils geringer als gedacht, z.B. von p0 = 961.22 Pa nach p0 + Δp2 = 967.55 Pa.


Der Überdruck zu Beginn des Experiments:

Danach die adiabatische Expansion auf Umgebungsdruck:

Und die isochore Druckerhöhung im Anschluss an die adiabatische Expansion:

Mit diesen Werten ergab sich dann folgender Adiabatenkoeffizient: 
Er lag mit κ = 1.22 deutlich zu niedrig. Für einen höheren Wert (Sollwert 1.4 für zweiatomige Gase wie Luft) hätte der isochore Druckanstieg um Δp2 deutlich höher ausfallen müssen. Man darf aber auch nicht vergessen, dass der zu Beginn eingestellte Überdruck Δp1 nur wenige mbar ausmacht. Daher ist die durch adiabatische Expansion erfolgte Temperaturabnahme äußerst gering. Die im Internet präsentierten, erfolgreichen Versuchsaufbauten unterscheiden sich aber doch recht deutlich von meinem Setup mit der Getränkeflasche und dem Fahrradventil. Aber es kann eben nicht jedes Experiment so laufen wie man sich das gerne wünscht 😉

