Die Maxwell-Boltzmann-Verteilung ist nach den beiden Physikern James Clerk Maxwell (1831–1879, https://de.wikipedia.org/wiki/James_Clerk_Maxwell) und Ludwig Boltzmann (1844–1906, https://de.wikipedia.org/wiki/Ludwig_Boltzmann) benannt, die diese Verteilung im Jahr 1860 erstmals hergeleitet haben. Die Verteilung gibt die Wahrscheinlichkeitsdichte in Abhängigkeit von der Geschwindigkeit für ein Gas bei einer bestimmten Temperatur T an. Wie man vermuten kann, kommt bei einem Gas nicht nur eine einzelne Geschwindigkeit v vor, sondern ganz unterschiedliche wie in dieser Abbildung angedeutet:
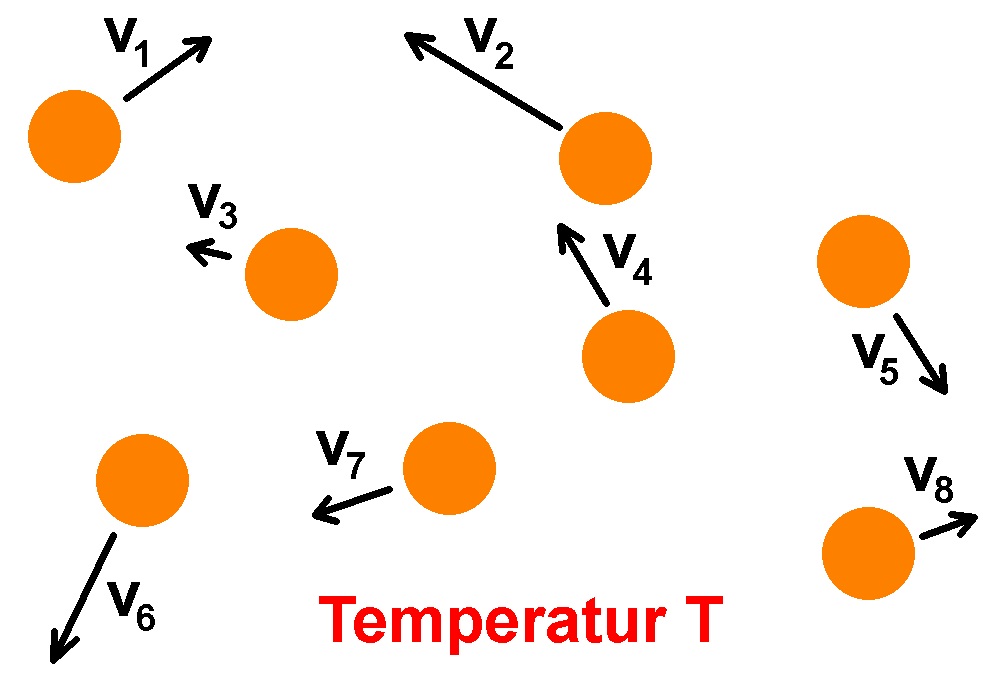
Die dazugehörige Wahrscheinlichkeitsverteilung sieht dann zum Beispiel so aus:
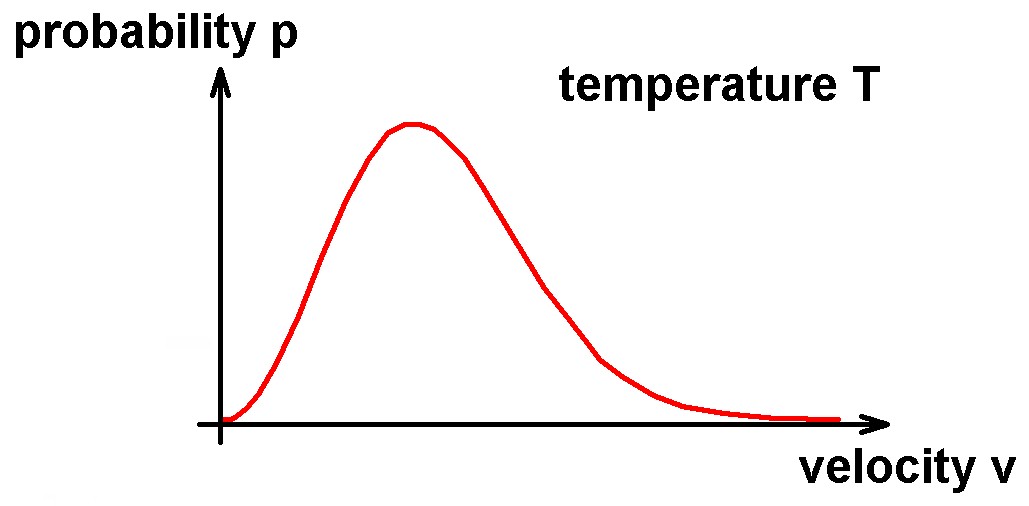
Diese Verteilung hängt wie man vermuten kann stark von der Temperatur T ab. Je höher die Temperatur des Gases, desto schneller bewegen sich die Gasteilchen im Mittel. Die Kurve/Verteilung flacht also mit zunehmendem T ab und breitet sich weiter nach rechts aus in Richtung höherer Geschwindigkeiten:
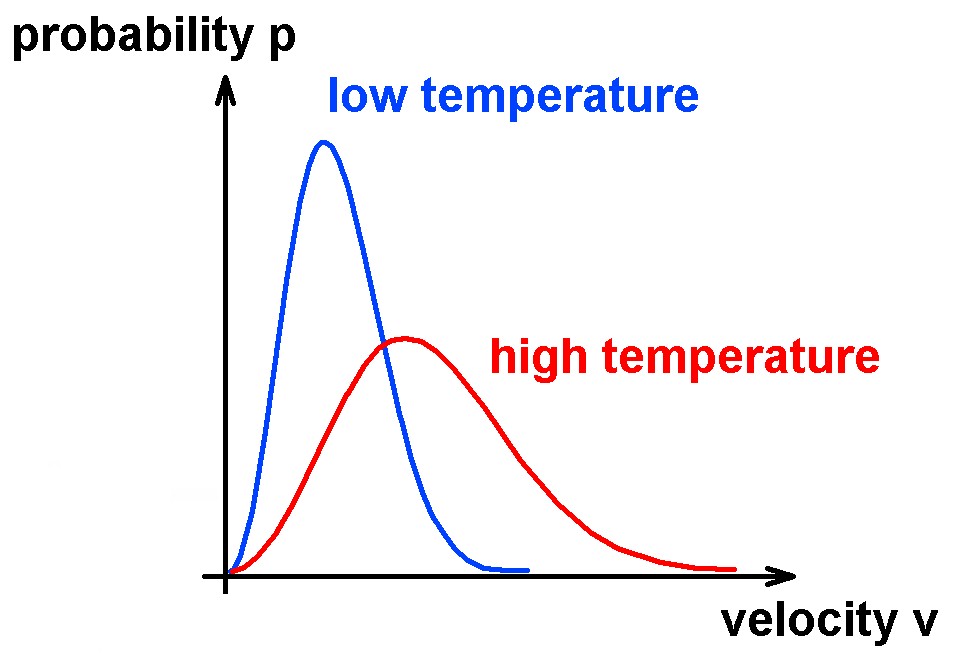
Anhand dieser Verteilung erkennt man, welche Geschwindigkeit bei einer gegebenen Temperatur am häufigsten auftritt (= Maximum der Kurve) bzw. man kann über die Wahrscheinlichkeitsdichte die mittlere Geschwindigkeit bzw. das mittlere Quadrat der Geschwindigkeit ausrechnen.

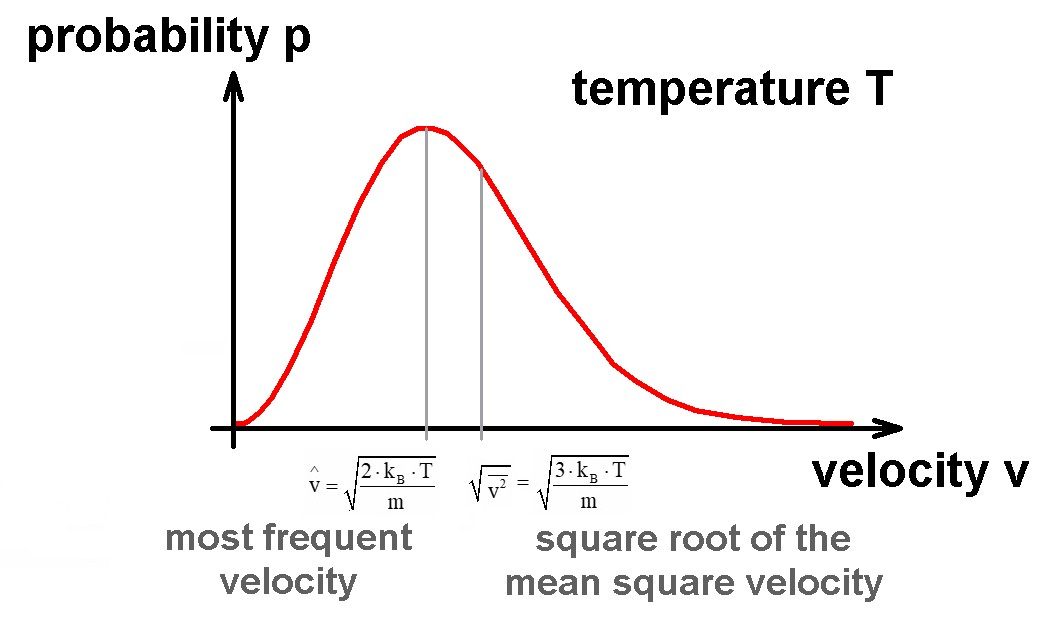
Mittels der mittleren quadratischen Geschwindigkeit lässt sich sehr einfach die mittlere kinetische Energie der Gasteilchen in Abhängigkeit von der Temperatur bestimmen. Es gilt dann die bekannte Beziehung Ekin = 3/2 · kB · T.
Dies ist quasi die Definitionsgleichung für die Temperatur T. Die Temperatur T (in Kelvin natürlich) ist ein Maß für die mittlere kinetische Energie der Teilchen. Eine hohe Temperatur bedeutet vereinfacht ausgedrückt schnelle Teilchen, eine tiefe Temperatur langsamere Teilchen. Bei T = 0 K (absoluter Temperaturnullpunkt) sinkt Ekin auf 0 ab, es gibt dann also überhaupt keine Bewegung mehr.
Bei Raumtemperatur beträgt die mittlere kinetische Energie 38 meV, unabhängig von der Masse der Gasteilchen! Leichte Teilchen besitzen demnach bei einer bestimmten Temperatur eine höhere mittlere Geschwindigkeit als schwere Teilchen. Deren mittlere kinetische Energie ist aber eben gleich! Damit dies nicht zu theoretisch wird gleich einmal eine kurze anschauliche Rechnung. Und zwar geht es um die häufigste Geschwindigkeit der Luftteilchen bei Raumtemperatur:

Diese beträgt immerhin 410 m/s = 1476 km/h, also mehr als die Schallgeschwindigkeit 😉
EXCEL-Simulation der Maxwell-Boltzmann-Verteilung, wobei man die Molmasse und die Temperatur eingeben kann:

Im folgenden Graphen sind die Geschwindigkeitsverteilungen für drei unterschiedliche Temperaturen dargestellt. Die Fläche unter der Kurve muss jeweils die Wahrscheinlichkeit 1 ergeben, da diese ja dann alle Teilchen mit all ihren möglichen Geschwindigkeiten umfasst. Deutlich erkennt man wieder, wie mit zunehmender Temperatur die Graphen nach rechts wandern also in Richtung höherer Geschwindigkeiten. Im konkreten Fall beziehen sich die Graphen auf molekularen Stickstoff N2 bei 0 °C, 100 °C und 1000 °C.

Bildquelle: https://de.wikipedia.org/wiki/Maxwell-Boltzmann-Verteilung#/media/Datei:Mb_N2.png, CC0
Experiment
Wie lässt sich nun diese Maxwell-Boltzmann-Verteilung experimentell überprüfen? Es gibt bereits leider sehr teure Aufbauten im Lehrmittelhandel. Diese kosten zum Teil mehr als 4000 Euro. Aber es geht zum Glück auch günstiger. Mein Ansatz bestand darin, für den Gasraum LEGO ® -Steine zu verwenden. Am Boden des Gasraums befindet sich eine bewegliche Platte, die mittels Motor und Zahnrädern rauf und runter bewegt wird. Dadurch erhalten die Gasteilchen (in meinem Fall kleine Stahlkugeln) ihren Impuls.

Hier der zum Einsatz kommende LEGO ® -Kolben:

Bezugsquelle 3D-Teile: https://www.etsy.com/at/shop/MZProduction, Email: mz-production@outlook.com




Hier sieht man die 1 mm Stahlkugeln, wobei ich befürchte, dass diese wohl zu klein für den Versuch sind. Aus diesem Grund habe ich auch noch Kugeln mit 1.5 mm, 2 mm, 2.5 mm und 3 mm Durchmesser bestellt.

Seitlich im Gasraum befindet sich ein dünner horizontaler Schlitz. Durch diesen gelangen die Stahlkugeln mit unterschiedlichen Geschwindigkeiten nach außen, wo sie der Schwerkraft folgend in einen Auffangbehälter mit einzelnen Schlitzen fallen. Ist ihre Geschwindigkeit größer, so legen sie während des Falls eine längere horizontale Strecke zurück und gelangen daher zu einem Auffangmodul weiter rechts. Auf diese Weise können die Stahlkugeln nach ihrer Geschwindigkeit sortiert werden. Im Boden der Auffangmodule befinden sich Rampen, welche die eingesammelten Kugeln entlang einer Rinne nach außen rollen lassen. Dort angekommen können sie dann gezählt werden. Im Idealfall erhalte ich eine zur Maxwell-Boltzmann-Verteilung ähnliche Anhäufung.


Die für den Aufbau benötigten LEGO ® -Teile habe ich erstmalig über BRICKLINK bestellt. Dies funktionierte reibungslos.



Den kompatiblen Motor habe ich günstig über Amazon bestellt. Es wird sich zeigen, ob er die Bodenplatte schnell genug nach oben und unten bewegen kann. Die Drehzahl bei 9 V liegt nämlich nur bei rund 170 U/min. Falls dies zu wenig ist, werde ich es mit einer Übersetzung mittels Zahnräder probieren. Sollte dies dann auch noch zu wenig sein, kann ich es noch immer mit einem anderen Elektromotor versuchen. Dann muss ich mich halt um die Verbindung der LEGO ® -Technikstange mit der Motorenachse kümmern.


Heute sind bereits die Motoren und die 2 mm Stahlkugeln angekommen und so konnte ich einen ersten Testlauf unternehmen. Den Motor schließe ich dabei nicht an die Batteriebox, sondern an ein regelbares Netzteil an. So kann ich die Geschwindigkeit schön steuern und zudem verbrauche ich keine Batterien.

Das Netzteil wird mit den beiden inneren Adern C1 und C2 verbunden:

Quelle: https://www.gutefrage.net/frage/wie-funktioniert-die-polung-von-einem-lego-functions-motor–


Da sich die Bodenplatte aber zu langsam bewegte, habe ich nun eine 1:3 Übersetzung mit Zahnrädern eingebaut. Damit springen die Kugeln munter im Gasraum herum und verlassen diesen auch wie erhofft durch den seitlichen Schlitz.




Jetzt fehlt eigentlich nur noch der 3D-gedruckte Auffangbehälter. Bin schon auf die Geschwindigkeitsverteilung gespannt und ob sie der Maxwell-Boltzmann-Verteilung ähnelt.
Mittlerweile ist der 3d-gedruckte Kugelauffangbehälter angekommen. Passt eigentlich alles perfekt. Lediglich das Gefälle der Rampe ist wohl eine Spur zu groß, sodass die Kugeln am Ende der Rinne zuviel Schwung besitzen und teilweise aus den Rinnen fliegen. Oben bei den Eintrittschlitzen kommt es auch mitunter vor, dass die Kugeln an den dünnen Rändern abprallen und dann erst in einen anderen Schlitz fallen. Ob dies sehr störend ist, wird sich experimentell erst zeigen.





Heute konnte ich den Versuch durchführen. Den LEGO ® -Aufbau habe ich noch ein wenig abgeändert. So erfolgt nun die Einführung der Stahlkugeln in den Gasraum etwas komfortabler und die Seite zum Kugelauffangbehälter habe ich abgeflacht, damit dieser nun ganz an den Turm heranrücken kann. Etwas mühsam war es, die vielen herausgesprungenen Kugeln wieder vom Boden einzusammeln. Mit dem Ergebnis bin ich aber einigermaßen zufrieden. Meine Kugelverteilungen steigen anfangs stark an und fallen dann in Richtung höherer Geschwindigkeiten langsamer ab. Gekostet hat mich der Spaß 100 Euro für die viel zu vielen LEGO ® – Steine, 25 Euro für zwei Motoren, 15 Euro für die Stahlkugeln und 25 Euro für den 3D-Druck, also in Summe 165 Euro. Wenn man bedenkt, dass dieser Versuch im Schulmittelhandel für stolze 4700 Euro angeboten wird, wieder einmal spottbillig 😉 Meine Schüler können dann zum Beispiel untersuchen, wie sich die Kugelverteilung ändert, wenn man die Motorspannung erhöht bzw. erniedrigt entsprechend einer Temperaturerhöhung/senkung.




Zum Abschluss noch das Youtube-Video:

