Bildquelle: https://de.wikipedia.org/wiki/Augustin_Fresnel
Augustin Jean Fresnel (1788 – 1827) war ein französischer Physiker und Ingenieur, der wesentlich zur Begründung der Wellentheorie des Lichts und zur Optik beitrug. Er studierte sowohl theoretisch als auch experimentell das Verhalten von Licht.
Die fresnelschen Gleichungen oder Formeln beschreiben quantitativ die Reflexion und Transmission einer ebenen, elektromagnetischen Welle mit einer bestimmten Polarisation (parallel bzw. senkrecht zur Einfallsebene) an einer ebenen Grenzfläche. Der zunächst berechnete Reflexions- und Transmissionsfaktor ist das Verhältnis der reflektierten bzw. transmittierten Amplitude zu jener der einfallenden Welle. Durch Quadrieren erhält man den Reflexions- bzw. den Transmissionsgrad, welche als Energiegrößen den gemessenen Intensitäten entsprechen.
Für die Reflexionsfaktoren je nach Polarisation gilt:
Mit Excel kann man diese Funktionen bzw. den Reflexionsgrad R (Quadrat von rs bzw. rp) sehr schön in Abhängigkeit der Brechungsindexe n simulieren:
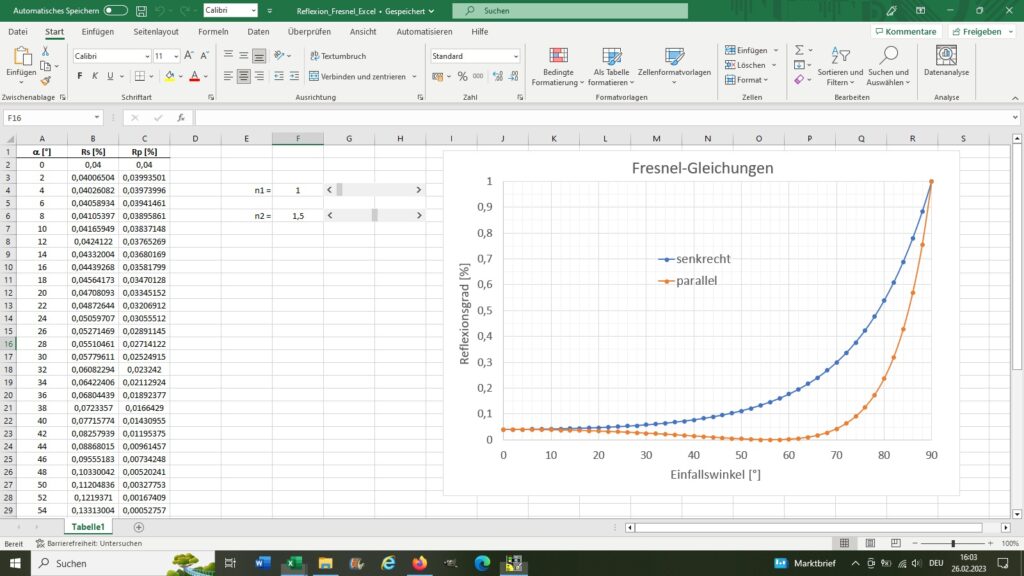
Wie man anhand des Diagramms sieht, beträgt bei senkrechtem Einfall (Einfallswinkel zum Lot ist 0°) der Reflexionsgrad beim Übergang Luft-Glas für beide Polarisationen 4 %. Für senkrechte Polarisation nimmt dann R mit zunehmenden Einfallswinkel kontinuierlich zu und erreicht bei streifenden Einfall (Einfallswinkel = 90°) mit 100% sein Maximum. Bei paralleler Polarisation ist dies etwas anders. Zunächst nimmt nämlich der Reflexionsgrad mit zunehmenden Einfallswinkel ab und erreicht beim sog. Brewsterwinkel (ca. 56° bei der Kombination Luft-Glas) mit 0 % sein Minimum. In diesem Fall wird also parallel polarisiertes Licht überhaupt nicht reflektiert! Danach nimmt der Reflexionsgrad R wieder zu und erreicht bei 90° Einfallswinkel ebenfalls wieder 100%.
Warum ist dies so? Im Brewsterwinkel stehen reflektierter Strahl und gebrochener Strahl aufeinander senkrecht. Die zur Abstrahlung angeregten Elektronen schwingen im Brewsterwinkel aber genau in Richtung des reflektierten Strahls. Genau entlang der Schwingungsrichtung strahlt aber ein Dipol keine elektromagnetischen Wellen ab. Deshalb gibt es hier keinen reflektierten Strahl!
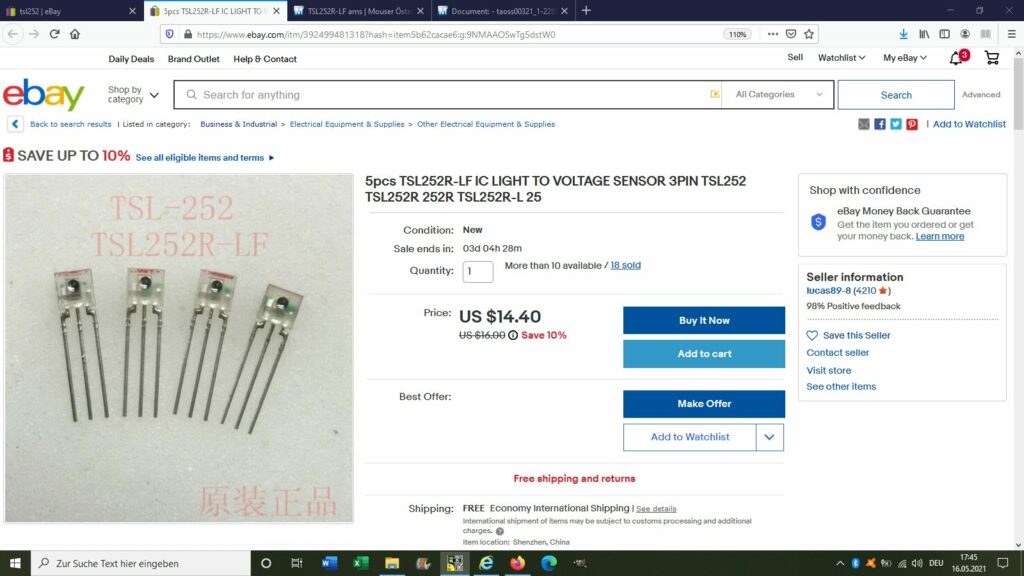
Für das Experiment wird parallel bzw. senkrecht zur Einfallsebene linear polarisiertes Laserlicht an einer Glasplatte reflektiert und die Intensitäten in Abhängigkeit vom Einfallswinkel α ermittelt. Der jeweilige Reflexionsgrad R ergibt sich einfach aus Irefl/I0. Die Intensitäten werden mit dem Lichtsensor TSL252R gemessen. Dieser besitzt nur drei Anschlüssen, Versorgungsspannung, Ground und Ausgang:
Hier der experimentelle Aufbau:
Experiment
Als Laser verwende ich eine grüne 520 nm Laserdiode mit rund 10 mW Leistung. Diese wird aber nicht bei voller Leistung betrieben, denn sonst würde der Lichtsensor bei flachen Einfallswinkeln und demnach starker Reflexion in Sättigung gehen.
Parallel zur Einfallsebene polarisiertes Licht vor dem Brewsterwinkel:
Parallel zur Einfallsebene polarisiertes Licht im Brewsterwinkel, R = nahezu 0:
Parallel zur Einfallsebene polarisiertes Licht nach dem Brewsterwinkel mit wieder zunehmender Intensität:
Hier nun die beiden Messreihen, einmal mit Polarisation parallel und dann senkrecht zur Einfallsebene. Durch die doch sehr kleine Sensorgröße des TSL252R war es manchmal nötig, den Sensor in der Höhe leicht zu repositionieren. Meine beiden Graphen entsprechen aber recht gut der Theorie…
Der erfassbare Einfallswinkelbereich liegt zwischen 5° und 77°. Darüber und darunter wird der Laserstrahl durch den Aufbau blockiert. Man erkennt bei paralleler Polarisation schön die Intensitätsabnahme auf U ≡ R ≈ 0% hin zum Brewsterwinkel, welcher bei rund 55° liegt.
Mittels Brewsterwinkel lässt sich dann noch der Brechungsindex des Glases bestimmen:
Zum Abschluss noch das Youtube-Video:
