
Bildquelle: https://de.wikipedia.org/wiki/Oberflächenspannung#/media/Datei:Wasserläufer_bei_der_Paarung_crop.jpg
Die Oberflächenspannung einer Flüssigkeit kommt dadurch zustande, dass auf ein Teilchen inmitten der Flüssigkeit von allen Seiten symmetrisch Kohäsionskräfte wirken, die sich gegenseitig kompensieren. An der Oberfläche ist dies allerdings anders. Hier wirken nur stärkere Kohäsionskräfte nach links, rechts und unten. Nach oben wirken die in der Regel deutlich schwächeren Adhäsionskräfte zwischen Flüssigkeit und Luft. Als Folge wirkt eine resultierende Kraft nach unten.

Die Oberflächenspannung σ ist nun definiert als Kraft pro Längeneinheit, also σ = F/l. Ergänzt man Zähler und Nenner durch eine Länge, so erhält man die Formel σ = F · l / (l · l) = Energie / Fläche. In der sich bildenden Grenzfläche steckt also eine bestimmte Energie. Dies ist dann auch der Grund, warum die Oberflächenspannung eine Minimierung der Energie = Minimierung der Grenzfläche bewirkt.
Um diese Minimierung der Oberfläche experimentell zu zeigen, benötigt man zum Beispiel nur 2 Metallkreise mit Halterung. Benetzt man diese mit Seifenblasenlauge und entfernt sie voneinander, bildet sich zwischen den beiden Metallschlaufen eine Minimaloberfläche. Die direkte Verbindung beider Schlaufen wäre ja ein Zylindermantel. Dieser besitzt aber eine größere Oberfläche als die leicht nach innen gewölbte Oberfläche!


Kann man dies auch theoretisch berechnen? Hierzu müssen wir zunächst die Mantelfläche eines beliebigen Rotationskörpers betrachten, wenn dieser um die x-Achse rotiert:

Für die Berechnung der Mantelfläche benötigt man also nur die Kenntnis der Funktion f(x) und deren Ableitung f ‚(x), wobei obiges Integral zu berechnen ist.
Für unser konkretes Beispiel mit den beiden Metallschlaufen gehen wir von einer sich ausbildenden Parabel mit der Funktionsgleichung f(x) = a + b·x² aus. Die beiden Metallbügel sollen einen Abstand H aufweisen. Daher muss zwischen den Grenzen -H/2 und +H/2 integriert werden. Damit lässt sich die Mantelfläche M in Abhängigkeit von a, b und H berechnen. Die Parabel muss allerdings auch noch durch 3 festgelegte Punkte verlaufen und zwar muss gelten: f(0) = R – T und f(±H/2) = R. Die maximale Einbuchtung der Seifenoberfläche betrage also T und die Seifenhaut muss natürlich in den Metallschlaufen an den Positionen (–H/2, R) und (+H/2, R) enden.

Man erhält also schlussendlich die Formel für die parabelförmigen Mantelflächen M in Abhängigkeit von R, H und T. Legt man R und H zum Beispiel mit 5 cm fest und variiert nur die Einbuchtung T so erkennt man, dass für eine bestimmte Einbuchtung im Bereich T = 0.8 cm die Oberfläche der Seifenhaut minimal wird. Sie beträgt dann 149.8 cm². Zum Vergleich: Würde die Seifenhaut die beiden Metallschlaufen direkt ohne Einbuchtung verbinden, so würde man einen gewöhnlichen Zylindermantel mit der nun größeren Oberfläche von 157.1 cm² erhalten!
Ich habe nun zwei solche Metallschlaufen mit einem Radius R = 5 cm gebastelt und diese im Abstand von 5 cm zueinander postiert. Wie man anhand nachfolgender Abbildung erkennen kann, wölbt sich die Seifenhaut wirklich im Bereich von maximal 0.8 cm nach innen. Theorie und Experiment stimmen also sehr gut überein…

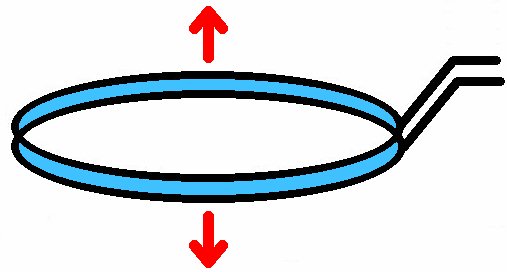
Wie ich Eingangs erwähnte, ist die Oberflächenspannung durch die Formel σ = Kraft / Länge definiert. Auf diese Weise lässt sie sich auch experimentell ermitteln. Man taucht einen Metallring in die zu untersuchende Flüssigkeit und zieht diesen dann langsam nach oben. Die sich zwischen Oberfläche und Ring bildende Haut zieht den Ring nach unten. Hängt der Ring an einem Kraftmesser, so kann die durch die Haut verursachte maximale Kraft F ermittelt werden. Die Gewichtskraft des Rings ist natürlich von der angezeigten Kraft abzuziehen. Als Länge L muss man den doppelten Ringumfang heranziehen. Doppelt deshalb, weil die Haut auf der Innen- und Außenseite angreift.




Der gesamte Messaufbau:




Die Messergebnisse:




Quelle: https://de.wikipedia.org/wiki/Oberflächenspannung
Laut Tabelle beträgt bei 20°C die Oberflächenspannung von Wasser 0.073 N/m. Mein Messergebnis liegt mit 0.076 nicht weit davon entfernt, zumal ja mein Wasser deutlich kälter als 20°C war, Heureka… 🙂
Einen netten Versuch zur Oberflächenspannung/Kapillarität kenne ich noch und zwar die Steighöhe von Wasser in einem schmalen Keil. Diesen Keil erzeugt man durch zwei Objektträger/Glasplatten, die an einem Ende einen bestimmten, kleinen Abstand aufweisen. In meinem Fall habe ich einfach eine 0.9 mm dünne Nadel eingespannt.






Der gesamte Versuchsaufbau:



Die Steighöhe h im Wasserkeil sollte indirekt proportional zum Plattenabstand d sein:

Um dies zu verifizieren habe ich ein Photo mit der Software Tracker vermessen:

Hier die Ergebnisse:


Trage ich die Steighöhe h gegen 1/d auf, so erhalte ich wie zu erwarten war eine Gerade:

Aus dem Geradenanstieg k lässt sich die Oberflächenspannung σ von Wasser ermitteln. Ich komme so aber nur auf einen Wert von 21 mN/m. Der Sollwert beträgt rund 70 mN/m für Wasser. Der Grund für die Abweichung ist mir im Moment noch nicht klar…

