
Bildquelle: Wikipedia
Das Babinet’sche Prinzip (auch Babinet’sches Theorem) ist ein Satz aus der Optik und besagt, dass die Beugungsbilder zweier zueinander komplementärer Blenden (beispielsweise Lochblende und eine kleine kreisrunde Scheibe) außerhalb des Bereiches, in den die geometrisch-optische Abbildung fällt (also die Abbildung ohne Beugungseffekte), gleich sind. Der Name geht auf den französischen Physiker Jacques Babinet (1794 – 1872) zurück, der das Theorem 1837 aufstellte.
In diesem Experiment werde ich konkret das Beugungsmuster eines Einzelspalts und jenes eines menschlichen Haars untersuchen. Sie sollten sich nach dem Babinetschen Prinzip also nicht unterscheiden, vorausgesetzt sie besitzen diesselbe Dicke.
Einzelspalt
Als Spalt verwende ich zwei Rasierklingen, welche auf einer Aluplatte montiert sind:



Laut Theorie gehorcht der Intensitätsverlauf hinter dem Spalt folgender Formel:

Für eine Wellenlänge λ = 532 nm und einer Spaltbreite b = 2 µm sieht das Intensitätsprofil wiefolgt aus:
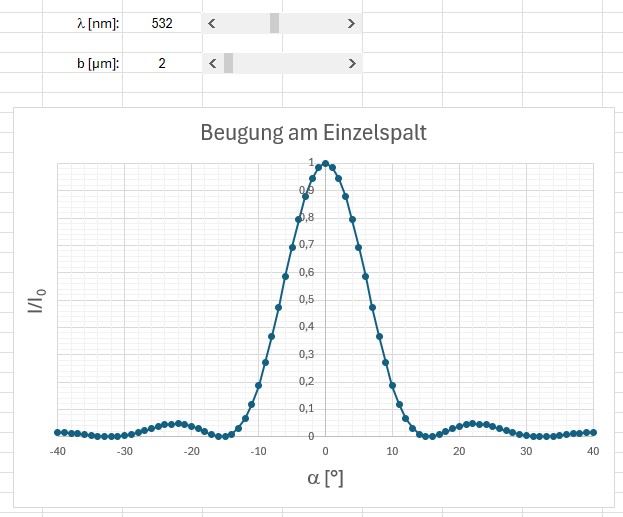
Für die Position der Minima gilt die einfache Beziehung: sin(α) = n · λ / b. Genau dieser Beziehung bediene ich mich dann später zur Ermittlung der Spaltbreite b.
Zunächst verwende ich einen grünen Laser bekannter Wellenlänge λ = 532 nm:






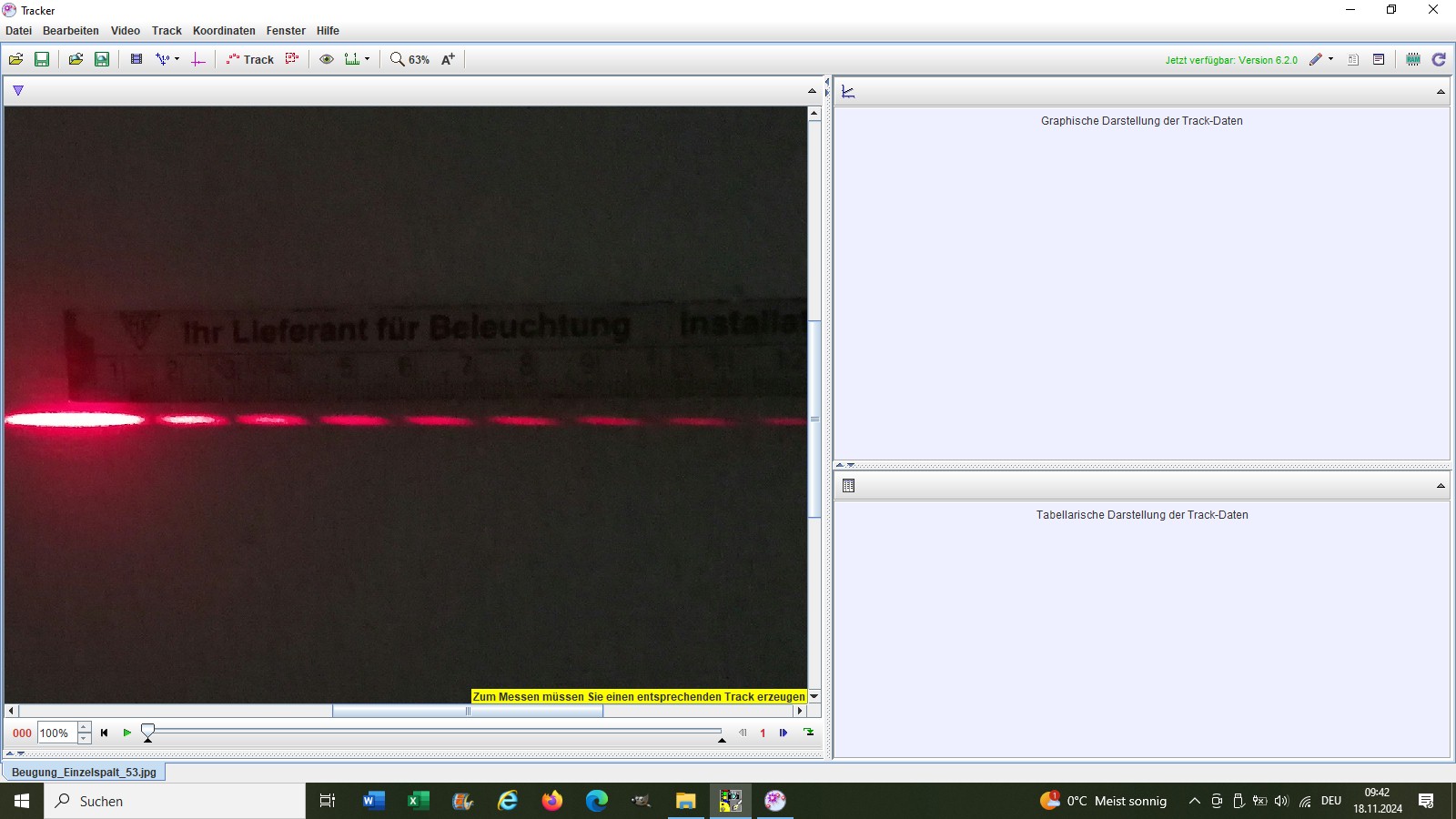
Zur Auswertung des Beugungsbildes verwende ich die Software Tracker (https://physlets.org/tracker/):
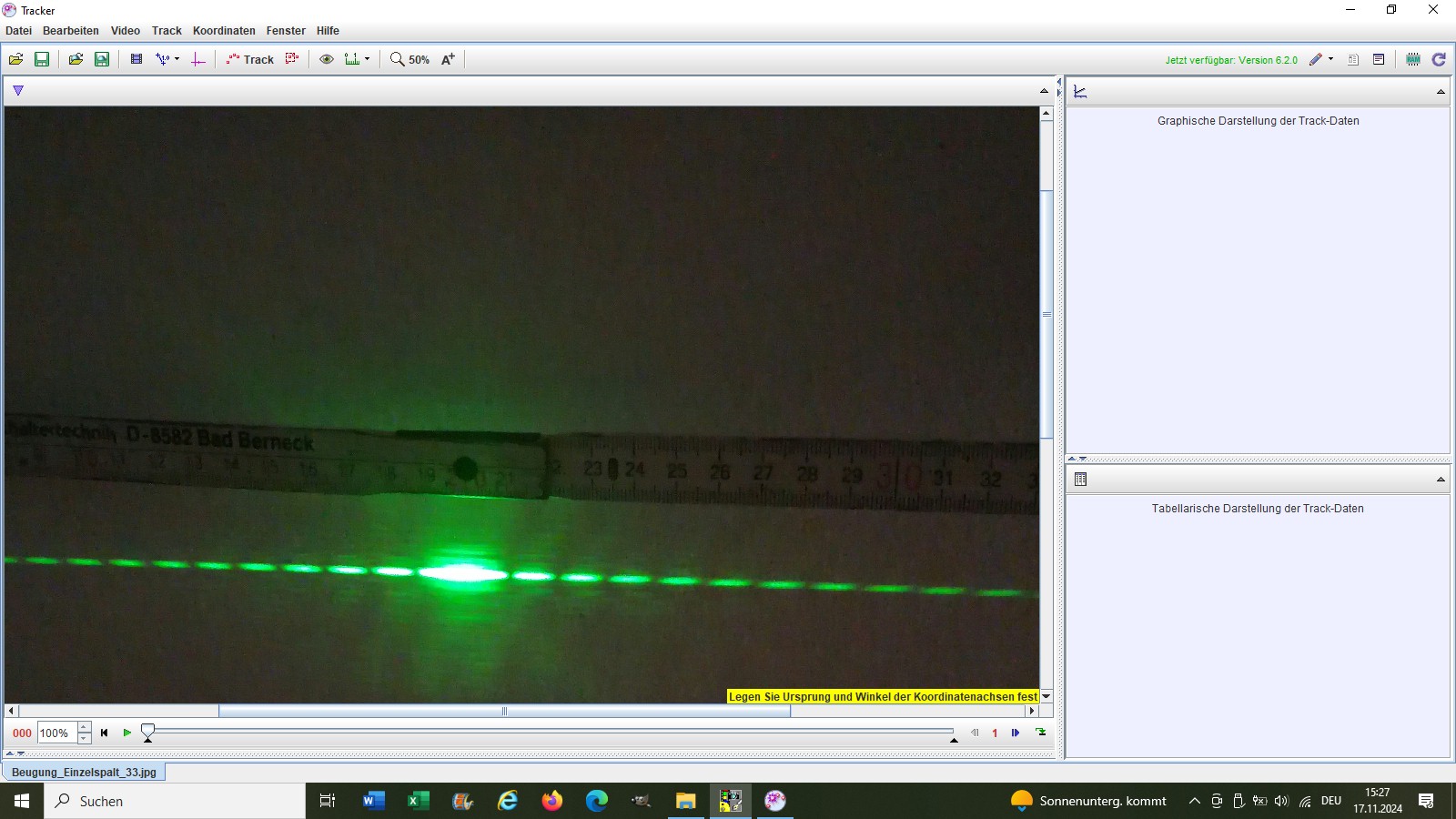
Zur Ermittlungs der Beugungswinkel α benötige ich neben der Strecke x an der Wand natürlich auch noch den Abstand d Spalt-Wand. Diesen konnte ich zu 127.5 cm bestimmen:


Zwischen der Wandstrecke x, dem Abstand d zwischen Spalt und Wand und dem Beugungswinkel α besteht der einfache Zusammenhang: tan(α) = x/d bzw. α = arctan(x/d).
Meine Messergebnisse und der zugehörige Graph sin(α) in Abhängigkeit von der Minimum-Ordnung n:
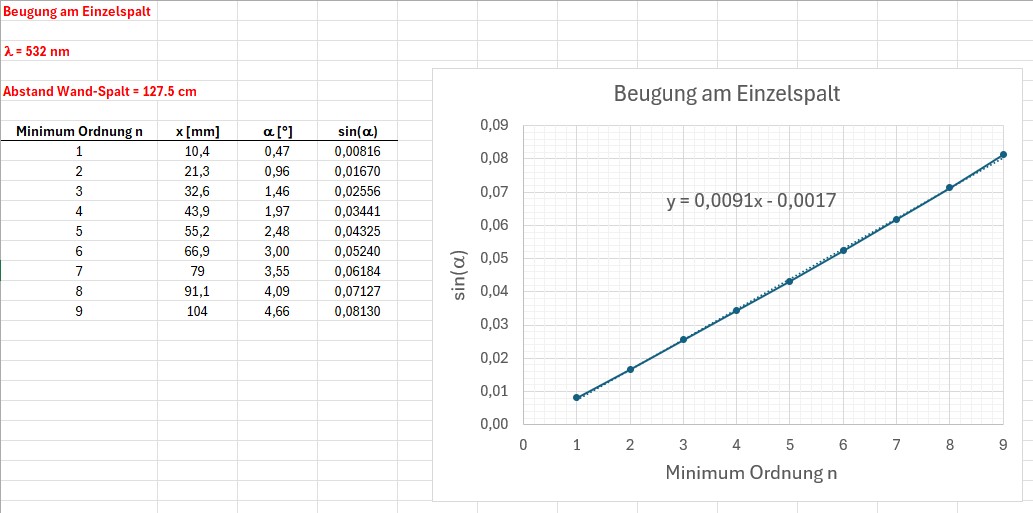
Mittels der Steigung k der erhaltenen Gerade wird dann die Spaltbreite b berechnet:

Ich komme also auf einen Wert von b = 58.5 µm. Mit diesem Wert kann ich dann zur Überprüfung neuerlich eine Simulation mit EXCEL starten:
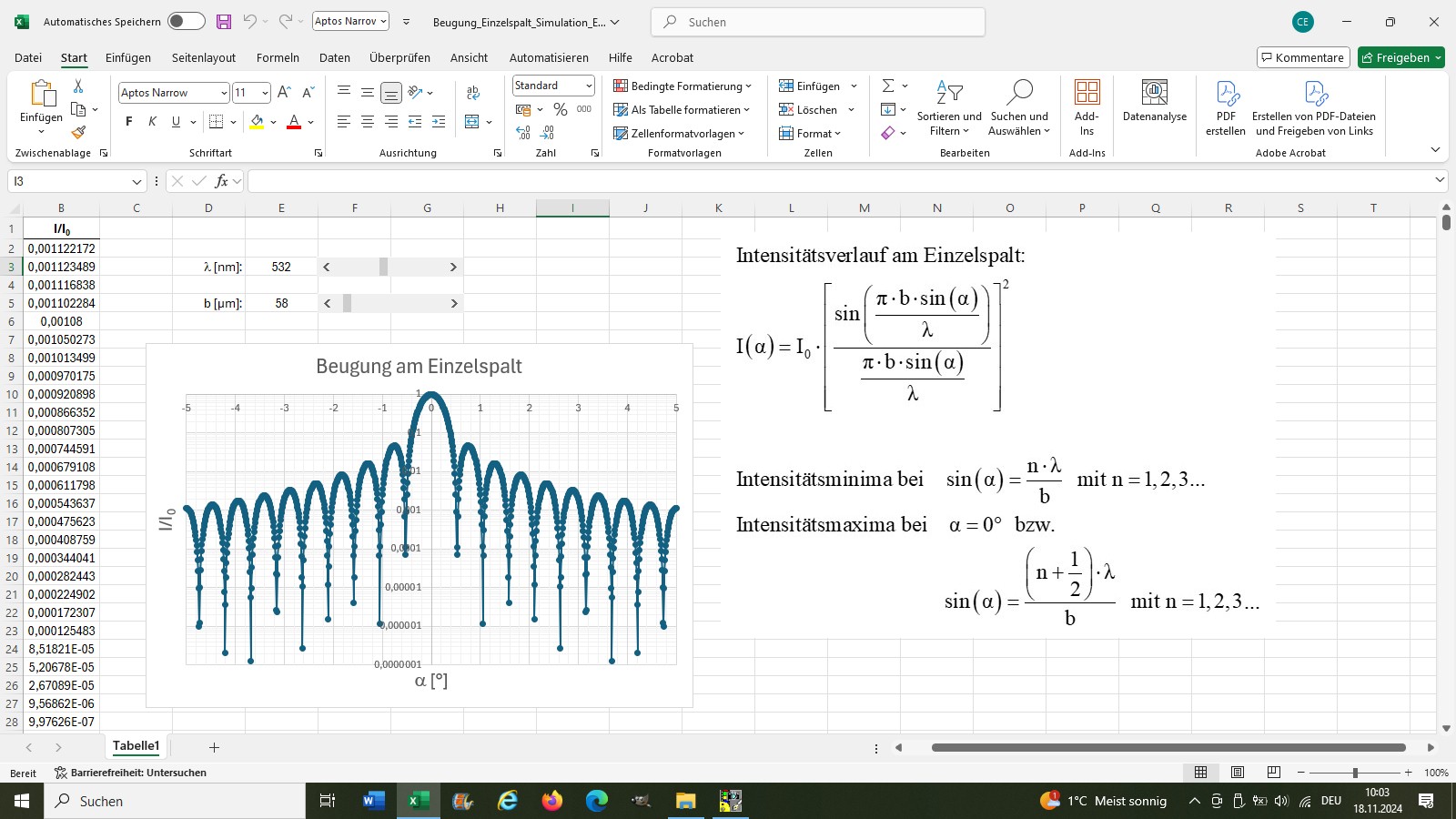
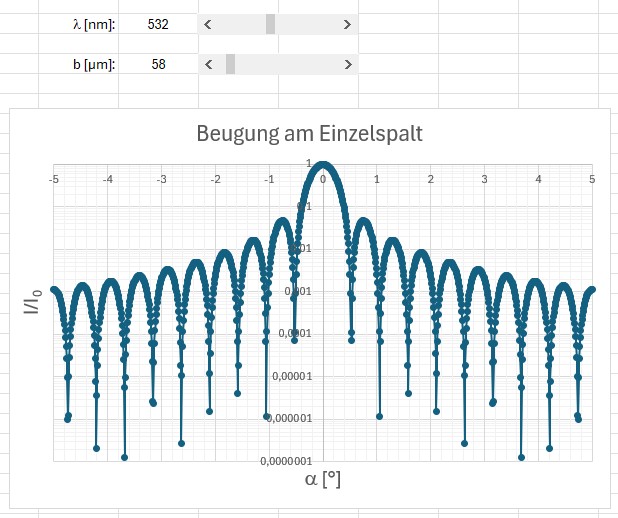
Kenne ich nun die Spaltbreite b, so kann ich zum Beispiel anhand des Beugungsbildes eines unbekannten Lasers dessen Wellenlänge λ bestimmen. Genau dies habe ich mit einem meiner roten Laser gemacht:




Die Vermessung erfolgte wieder mit der Software Tracker:
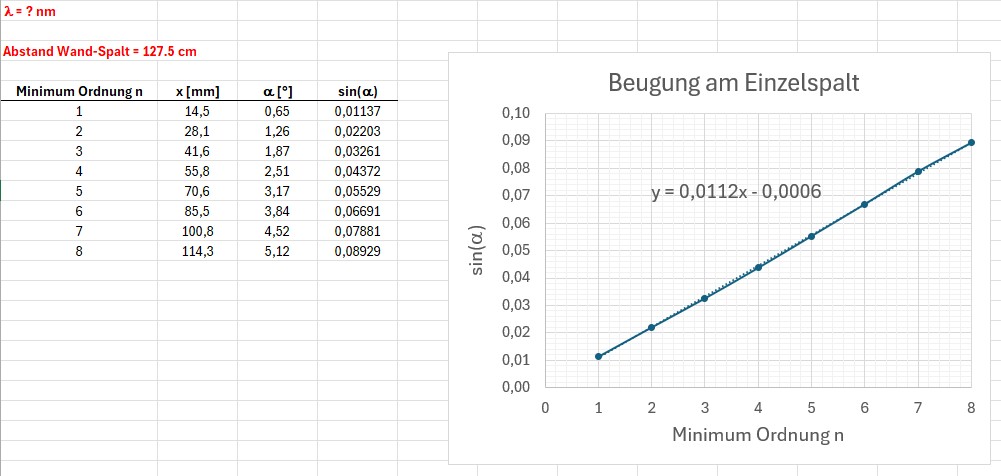
Der Geradenanstieg beträgt in diesem Fall k = 0.0112. Bei einem Laser mit größerer Wellenlänge fächert das Beugungsmuster weiter auf als bei einem Laser kürzerer Wellenlänge:

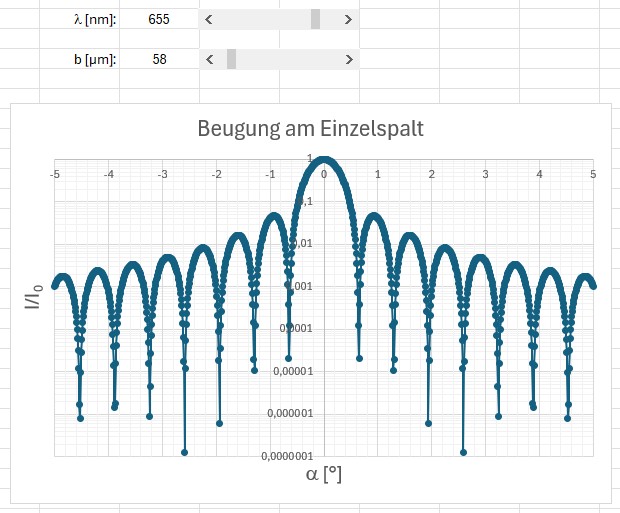
Der erhaltene Wert von λ = 655 nm für den roten Laser ist sehr plausibel, Heureka 😉
Hier noch die entsprechende Simulation für eine Wellenlänge von 655 nm und einer Spaltbreite von 58 µm:
Haar
Nun geht es um das Beugungsbild eines Haars. Zum Glück besitze ich noch ein paar wenige auf meinem Kopf für dieses Experiment. In wenigen Jahren werde ich aber diesen Versuch wohl nicht mehr machen können 😉
Der sehr simple Versuchsaufbau:
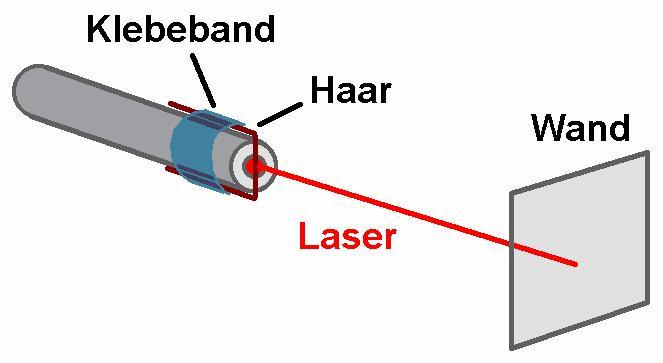
Der grüne Laserpointer mit dem vor der Öffnung fixierten Haar:


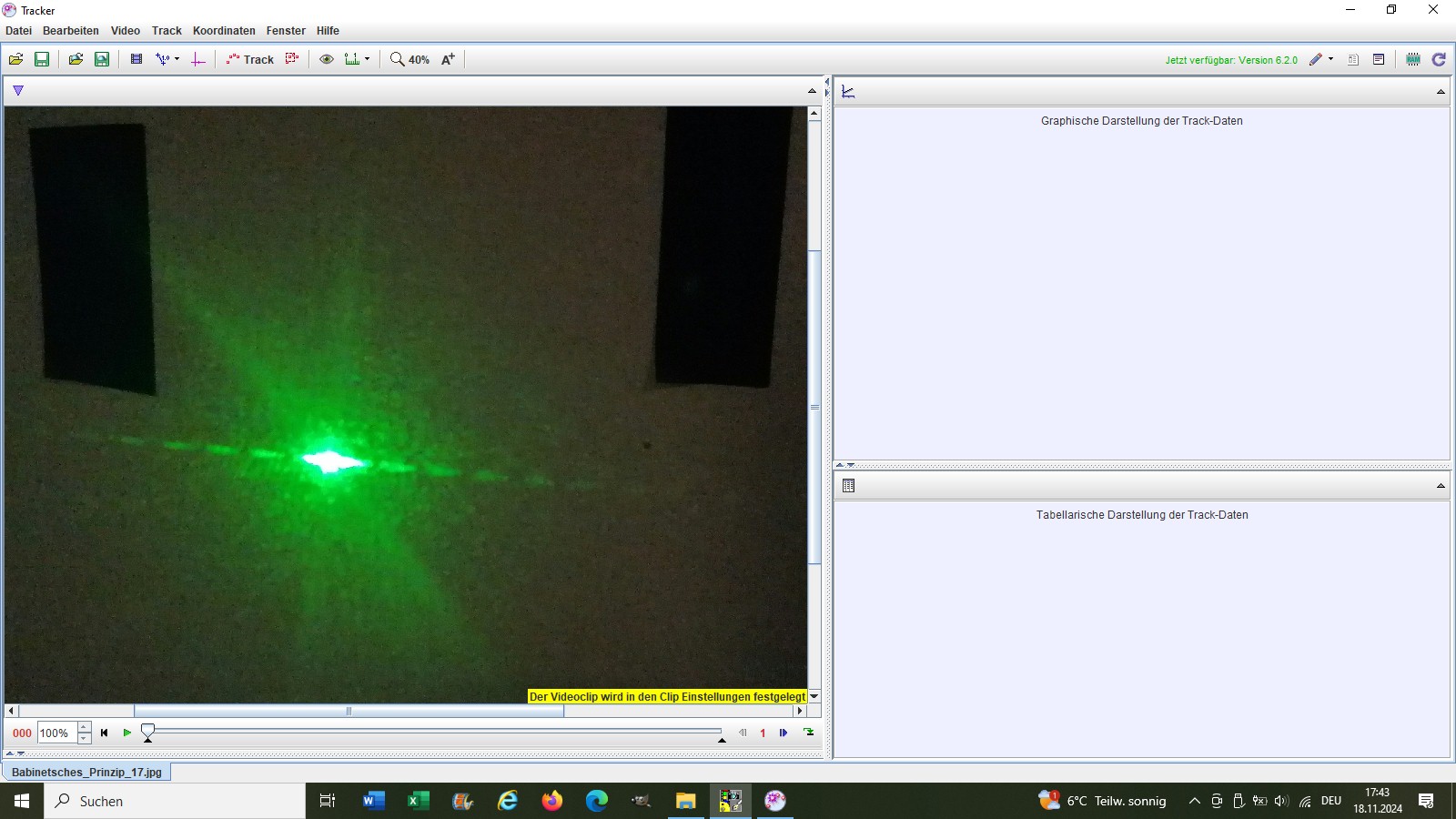
Das Beugungsbild auf der Wand:

Die beiden Klebestreifen haben einen Abstand von genau 10 cm. Dies benötige ich dann für die Ausmessung des Beugungsmusters:

Die Messergebnisse:
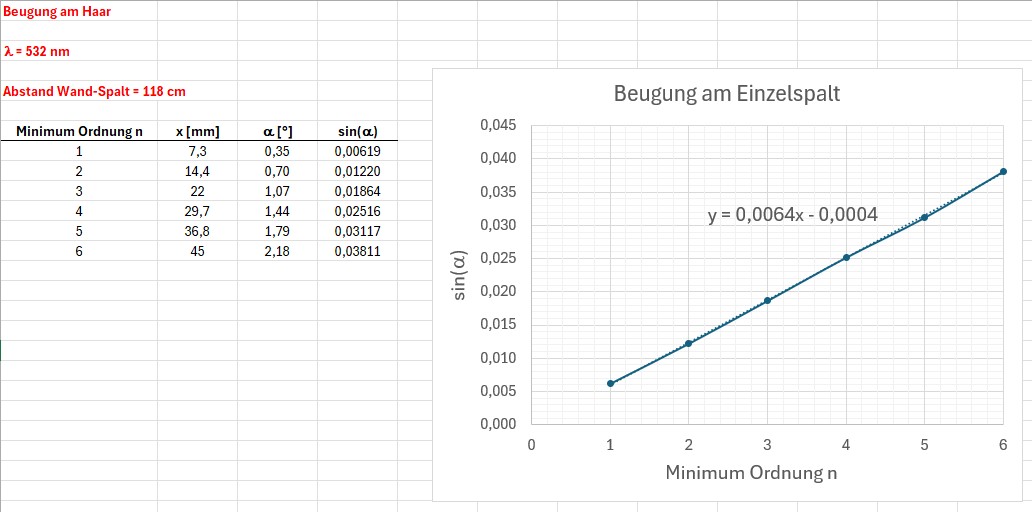
Die Berechnung der Haardicke:

Das Ergebnis deckt sich recht gut mit den Sollwerten für menschliches Haar:

Zum Abschluss noch der bildliche Beweis des Babinet’schen Prinzips: Die Beugungsbilder von Einzelspalt und Haar sind in der Tat vom Prinzip her ident bzw. bei Spaltbreite = Haardicke sogar gleich, voila…

Das Youtube-Video reiche ich wie immer nach…

