Alle hier vorgestellten Methoden zur Bestimmung der spezifischen Elektronenladung e/m (e…Elementarladung, m…Elektronenmasse) basieren auf der Bewegung von Elektronen in einem Magnetfeld mit der Flussdichte B. Bewegt sich ein Elektron mit der Geschwindigkeit v senkrecht zum Magnetfeld B, so vollführt es eine Kreisbahn mit dem Radius r. In diesem Fall ist die notwendige Zentripetalkraft Fzp gleich der Lorentzkraft FL. Es gilt also:
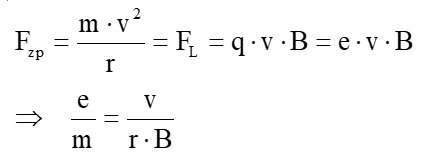
Kennt man also die Geschwindigkeit v, den Bahnradius r und die Flussdichte B, so kann man daraus die spezifische Elektronenladung e/m berechnen.
Die Geschwindigkeit v bzw. kinetische Energie Ekin der Elektronen ergibt sich aus der Beschleunigungsspannung U. Es gilt:
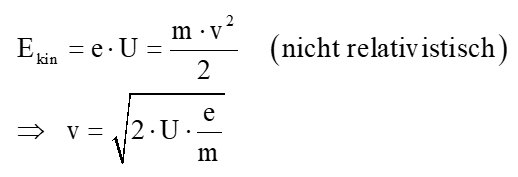
Setzt man dies oben in den Ausdruck für e/m ein, erhält man:

Die Flussdichte B im Inneren einer Zylinderspule mit n Wicklungen und der Länge L hängt wiefolgt von der Stromstärke I durch die Spule ab:

Variante 1: Elektronenröhre
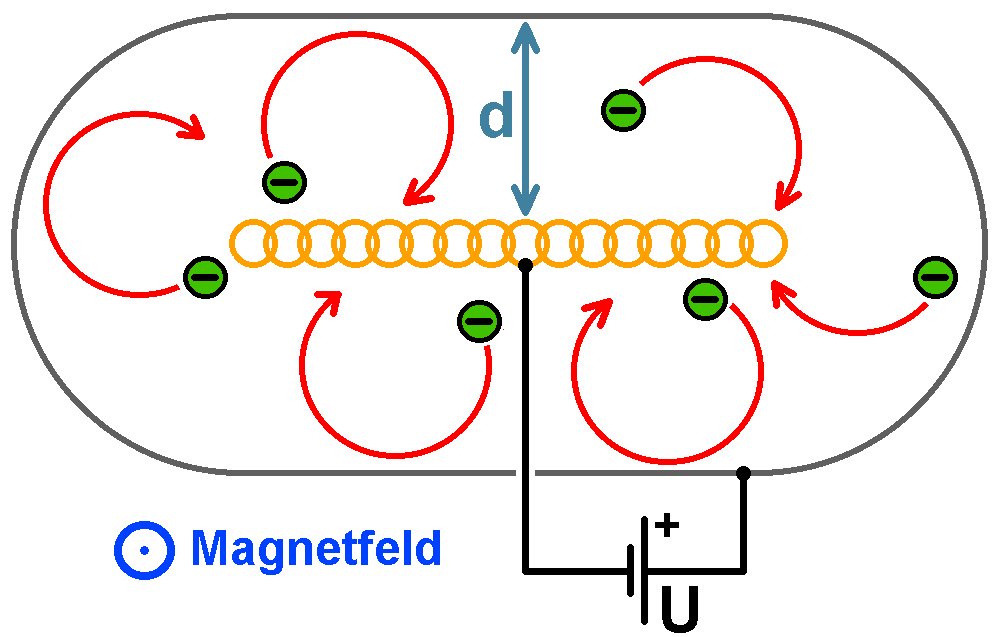
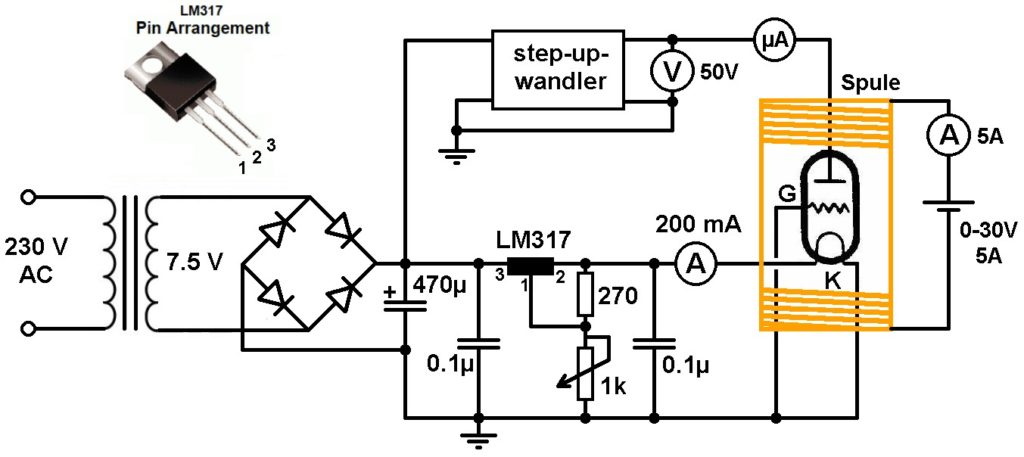
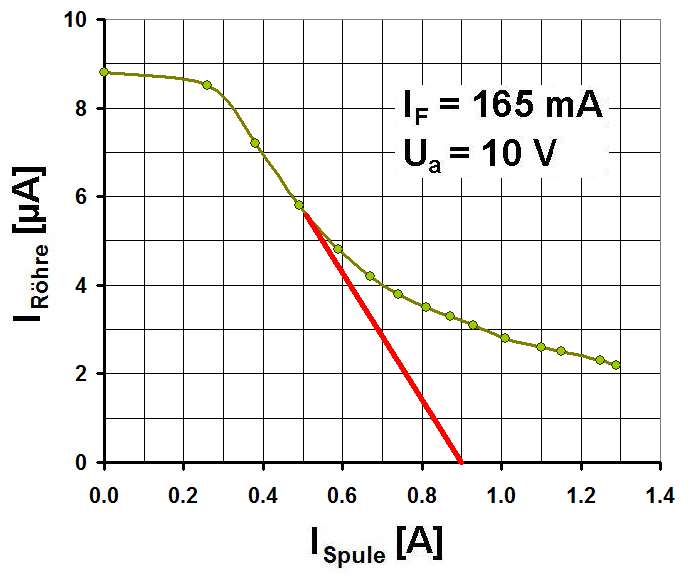
Mit einer alten Elektronenröhre RE 144 und einer Spule zur Erzeugung eines Magnetfelds lässt sich die spezifische Elektronenladung e/m bestimmen. Man gibt die Röhre ins Innere der Spule und misst den Röhrenstrom I in Abhängigkeit vom Magnetfeld B, sprich in Abhängigkeit vom Spulenstrom I.
Je größer die Stromstärke I durch die Spule, desto stärker wird das Magnetfeld B und desto kleiner wird der Bahnradius r der Elektronen. Ab einer bestimmten Stromstärke durch die Spule ist der Bahnradius so klein, dass die von der Kathode emittierten Elektronen nicht mehr zur Anode gelangen. Ab diesem Zeitpunkt sinkt der Röhrenstrom stark ab. Aus dem Spulenstrom, bei dem defacto kein Röhrenstrom mehr fließt, kann schlussendlich e/m berechnet werden.

Bildquelle: https://commons.wikimedia.org/wiki/File:Telefunken_re144_1937.jpg, Autor: Hihiman, GNU Free Documentation license














Variante 2: Magic eye tube
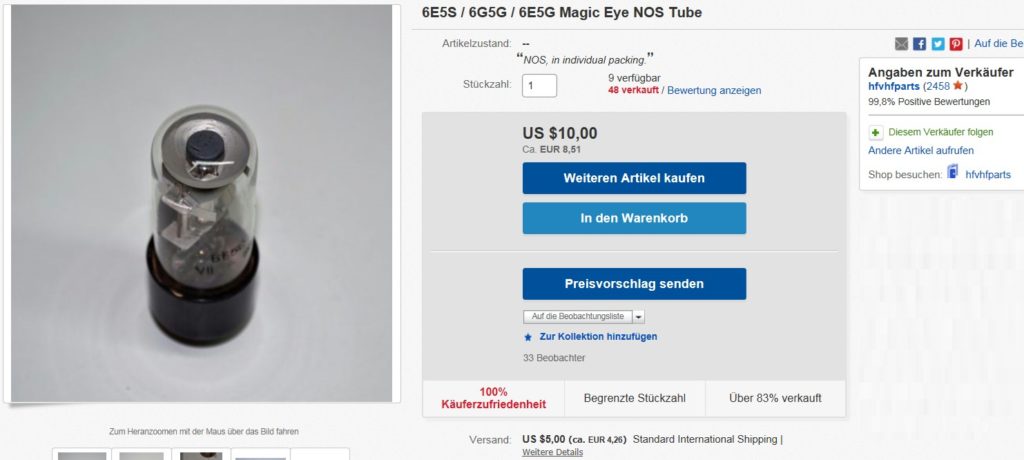
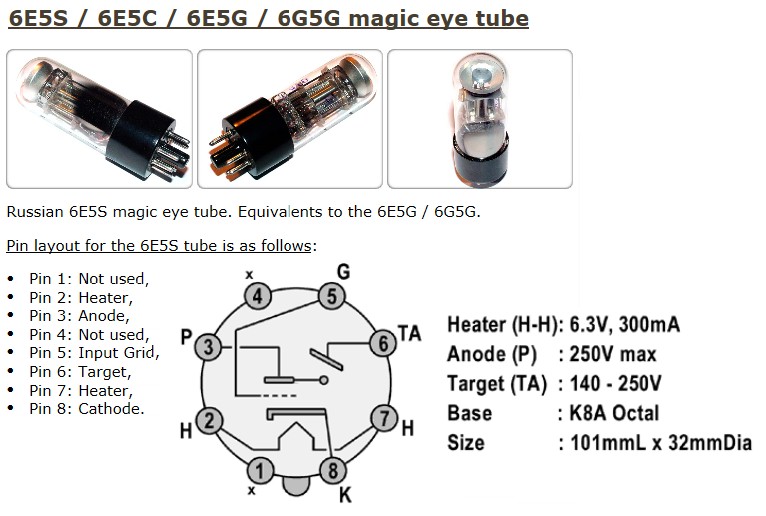
Dieser Versuch mit einer sog. magic eye tube funktioniert vom Prinzip her ähnlich wie die Variante 1. Man bringt die Spezialröhre wieder ins Innere einer Spule, welche für ein (homogenes) Magnetfeld sorgt. Die kreisförmige Bewegung der emittierten Elektronen kann man bei einer magic eye Röhre dadurch schön erkennen, da sie beim Auftreffen auf eine Leuchtschicht diese zum Leuchten anregen. So entsteht von oben betrachtet eine kreisförmige Abgrenzung der Leuchterscheinung. Deren Radius r kann man bestimmen und bei gegebener Beschleunigungsspannung und magnetischen Flussdichte B wieder die spezifische Elektronenladung e/m ermitteln. Zum Einsatz kommt bei meinem Experiment die russische Röhre vom Typ 6E5S/6E5C.
Es gilt wieder: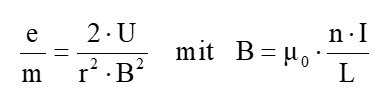
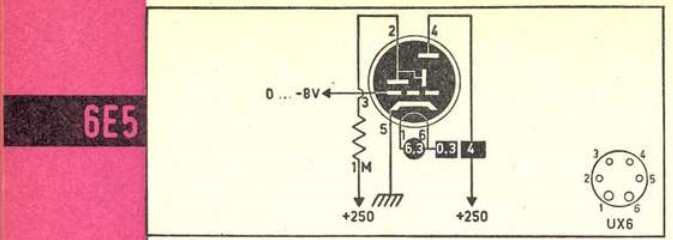
Die im Schaltplan eingezeichneten 250V an Target und Anode werden mittels Trafo bereitgestellt und sind ebenso wie die 0…–8V am Gate veränderbar! Je höher die Beschleunigungsspannung U, desto schneller sind die Elektronen und desto größer wird ihr Kreisbahnradius r.










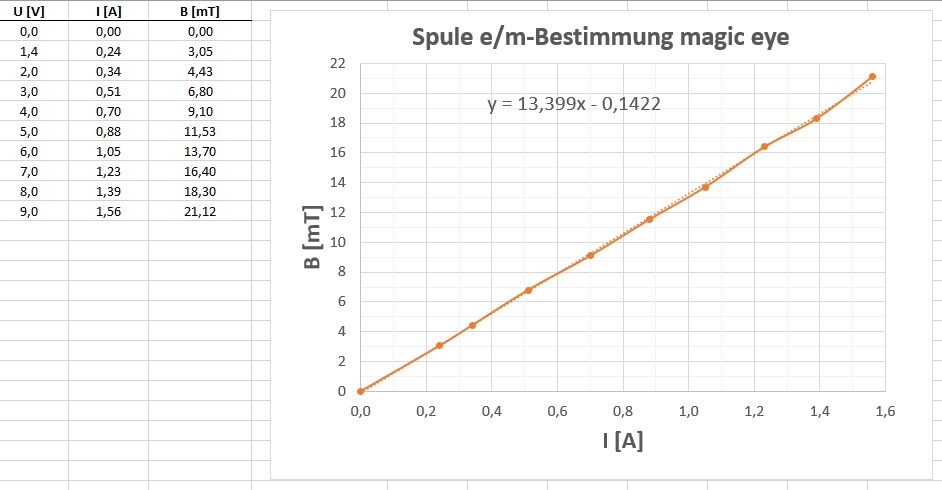
So, mittlerweile habe ich die Spule mit dem 0.6 mm Kupferlackdraht gewickelt. Sie besitzt einen Widerstand von 5.6 Ω und eine Induktivität von 9,15 mH. Bei einem Strom von 1 A wird ein Magnetfeld von 13.4 mT erzeugt. Damit können die Schüler anhand der aktuellen Stromstärke die magnetische Flussdichte leicht ausrechnen.




Die Elektronenröhre passt wunderbar in die Spule…





Damit erziele ich bei einer Spulenspannung von 1 V einen Bahnradius der Elektronen von rund 2 cm, bei 10 V sind es dann nur noch 0.2 cm. Das passt sehr gut…

Die Messungen mit der magic eye tube sind auch im Kasten. Ströme im Bereich 0-1 A erweisen sich als sinnvoll. Die aus dem Bahnradius r ermittelte spezifische Elektronenladung e/m weicht allerdings relativ deutlich vom Sollwert ab. Aber es geht ja ums Prinzip und wenn man den geringen Preis des Aufbaus mit kommerziellen Fadenstrahlröhren vergleicht, so ist die Abweichung doppelt verschmerzbar. 😉










Das Youtube-Video zum Experiment:
Variante 3: Ringmagnet
Bei dieser Variante zur Bestimmung von e/m benötigt man eine DC-Hochspannung und 2 große Ringmagnete. Die Hochspannung erzeuge ich mit einer Zerhackerschaltung auf Basis des NE555 und einem DC-Zeilentrafo. Diesen findet man in alten Röhrenfernsehern. Die beiden HV-Ausgänge des Zeilentrafos postiert man im Inneren der Ringmagnete. Die durch die Spannung beschleunigten Elektronen bewegen sich im Magnetfeld B im Inneren der Ringmagnete entlang von Kreisbahnen mit dem Radius r. Mit diesem, der Beschleunigungsspannung U und der Flussdichte B lässt sich wieder die spezifische Elektronenladung e/m bestimmen. Die Stärke des Magnetfelds im Inneren der Ringmagnete bestimme ich mit einem selbst gebauten Teslameter (https://stoppi-homemade-physics.de/magnetometer/). Konkret ergab die Messung B = 0.05 T.
Die Ringmagnete besitzen die Abmessungen 40x20x10 mm bzw. 45x22x9 mm. Diese habe ich über Amazon besorgt.
Die Hochspannung lässt sich über die maximale Länge der Überschläge abschätzen. Entladungen von 1 cm entsprechen in etwa einer Spannung von 10 kV. Man kann die Spannung aber auch über einen hochohmigen Spannungsteiler (z.B. 1:1000) und einem Multimeter ermitteln.
Man erkennt schön, dass sich die Krümmungsrichtung der schnellen Elektronen umkehrt, wenn man die Ringmagnete umdreht, sprich die Richtung des Magnetfelds um 180° verändert.















