Bildquelle: https://mig.reisen/zentrifugentraining/

Hat man im Physikunterricht aufgepasst so weiß man, dass man unter der Beschleunigung die zeitliche Geschwindigkeitsänderung versteht. Es gilt also: a = dv/dt = v'(t). Nimmt also die Geschwindigkeit zu (Beschleunigung) oder ab (Bremsen), so beschleunigt man. Wie sieht es aber nun bei einer Kreisbewegung zum Beispiel mit konstanter Winkelgeschwindigkeit ω und demnach auch Bahngeschwindigkeit v aus? Da die Geschwindigkeit ja konstant ist könnte man meinen, dass es sich hier um keine beschleunigte Bewegung handelt. Dem ist aber nicht so. Denn wir müssen die Geschwindigkeit als Vektor betrachten. Dieser Geschwindigkeitsvektor kann nun vom Betrag her wachsen oder schrumpfen, aber auch seine Richtung ändern. In all diesen Fällen kommt es zu einer Beschleunigung. Bei einer Kreisbewegung spricht man von der sog. Zentripetalbeschleunigung.

Wie man anhand der Skizze erkennen kann, sind die Geschwindigkeitsvektoren v₁ und v₂ nicht ident, denn sie besitzen zwar hier in diesem Fall die gleiche Länge (Betrag), aber unterschiedliche Richtung!

Der Verbindungsvektor der beiden Geschwindigkeitsvektoren entspricht genau der Geschwindigkeitsänderung Δv = v₂ – v₁. Dieser ist durch a = Δv/Δt proportional zur Beschleunigung a!

Von welchen Größen und wie hängt nun diese Zentripetalbeschleunigung a_zp  ab? Sie wird von der Winkelgeschwindigkeit ω und vom Bahnradius r abhängen. Betrachten wir zunächst den Fall ω = konstant:

Eine Verdopplung des Bahnradius r bei konstanter Winkelgeschwindigkeit ω bedingt also eine Verdopplung der Beschleunigung a. Es muss also gelten: a_zp ≡ r.

Wie sieht es nun bei konstantem Bahnradius r und veränderter Winkelgeschwindigkeit aus?

Eine Verdopplung von ω bei gleichem Bahnradius r bewirkt also eine Vervierfachung der Zentripetalbeschleunigung. Daher muss gelten: a_zp ≡ ω².

Die Zentripetalbeschleunigung muss also folgende grafische Abhängigkeiten zeigen:

Beschleunigt ein Körper mit a, so muss auf ihn nach der Newtonschen Bewegungsgleichung die Kraft F = m·a wirken. Die Zentripetalbeschleunigung a_zp kennen wir ja nun. Daher folgt für die zugehörige Zentripetalkraft F_zp:

---

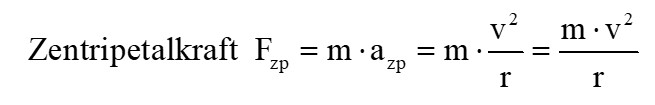
Experiment:

Für den Arduino gibt es ja eine Unmenge an Sensoren, zum Beispiel den MPU6050. Dabei handelt es sich um eine Kombination aus Beschleunigungssensor und Gyroskop (Winkelgeschwindigkeitsmesser). Das macht ihn ideal geeignet für dieses Experiment, denn wir wollen ja u.a. die Abhängigkeit der Zentripetalbeschleunigung von der Winkelgeschwindigkeit erfassen. Da man bei einer Rotation den Arduino nicht so einfach über Kabel auslesen kann, muss man sich eine andere Art der Datenübertragung ausdenken. Hierfür bietet sich Bluetooth an. Mit dem HC-05 gibt es auch ein kostengünstiges Modul genau für diesen Zweck.

Als Empfänger eignet sich bestens ein Smartphone. Man muss lediglich die App Arduino Bluetooth Terminal installieren und schon kann man auf einfachste Weise bis zu 6 Sensoren per Funk auslesen…

In meinem Fall lasse ich mir die drei Beschleunigungen a_x, a_y und a_z bzw. die drei Winkelgeschwindigkeiten ω_x, ω_y und ω_z am Smartphone anzeigen:

Nachdem ich den Motor besorgt habe, konnte ich den Aufbau finalisieren und das Experiment durchführen:

Hier die Messwerte in Ruhe, wobei auf a_x und g_z zu achten ist:

…und hier in Bewegung:

Die Zentripetalbeschleunigung zeigt wie erwartet eine lineare Abhängigkeit vom Bahnradius r

und eine quadratische Abhängigkeit von der Winkelgeschwindigkeit ω

Zum Abschluss noch das Youtube-Video: